Engage NY Eureka Math 3rd Grade Module 1 Lesson 7 Answer Key
Eureka Math Grade 3 Module 1 Answer Key
Eureka Math Grade 3 Module 1 Lesson 7 Problem Set Answer Key
Question 1.
a. Draw an array that shows 6 rows of 2.
b. Write a multiplication sentence where the first factor represents the number of rows.
________ × ________ = ________
Answer:
a.
Explanation:
Drawn an array that shows 6 rows of 2 as 6 × 2 as shown above in the picture.
b. Multiplication sentence where the first factor represents the number of rows as 6 × 2 = 12.
Explanation:
Wrote a multiplication sentence where the first factor represents the number of rows as 6 × 2 = 12.
Question 2.
a. Draw an array that shows 2 rows of 6.
b. Write a multiplication sentence where the first factor represents the number of rows.
____2____ × ____6____ = ___12_____
Answer:
a.

Explanation:
Drawn an array that shows 2 rows of 6 as 2 × 6 as shown above in the picture.
b. Multiplication sentence where the first factor represents the number of rows as 2 × 6 = 12.
Explanation:
Wrote a multiplication sentence where the first factor represents the number of rows as 2 × 6 = 12.
Question 3.
a. Turn your paper to look at the arrays in Problems 1 and 2 in different ways. What is the same and what is different about them?
b. Why are the factors in your multiplication sentences in a different order?
Answer:
a. Same is the result because both have the same value as 12, Different is number of rows and number of columns are not the same,
Explanation:
Turned my paper to look at the arrays in Problems 1 and 2 in different ways.
Is the same because both got same results as 12 and different about them is in problems 1 and 2 the number of rows and number of columns are not the same as one is 6 rows × 2 columns and in other it is 2 rows × 6 columns.
b. The factors in my multiplication sentences are in a different order because first we are taking 6 rows × 2 columns and in other it is 2 rows × 6 columns.
Explanation:
The factors in my multiplication sentences are in a different order because first we are taking 6 rows X 2 columns and in other it is 2 rows × 6 columns,
So, rows and columns differ in the both.
Question 4.
Write a multiplication sentence for each expression.
You might skip-count to find the totals.

 Explanation:
Explanation:
Wrote a multiplication sentence for each expression as shown above, might have skipped-count to find the totals.
Question 5.
Write and solve multiplication sentences where the second factor represents the size of the row.

 Explanation:
Explanation:
Wrote and solved multiplication sentences where the second factor represents the size of the row as
2 × 4 = 8 and 4 × 2= 8.
Question 6.
Ms. Nenadal writes 2 × 7 = 7 × 2 on the board.
Do you agree or disagree? Draw arrays to help explain your thinking.
Answer:
Yes, I agree Ms. Nenadal writings as 2 × 7 = 7 × 2,
Explanation:
Given Ms. Nenadal writes 2 × 7 = 7 × 2 on the board,
Yes, I agree because 2 × 7 = 14 and 7 × 2 = 14,
Drawn arrays to help and explained my thinking as shown above.
Question 7.
Find the missing factor to make each equation true.
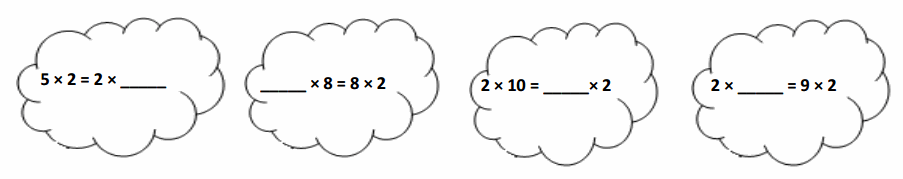
Explanation:
Found the missing factor to make each equations true as below
5 × 2 = 2 × 5,
As each equation is true, so the missing factor in 2 X ___ is 5 as LHS is equal to RHS, So 5 X 2 = 2 X 5.
2 × 8 = 8 × 2,
As each equation is true, so the missing factor in ___ X 8 is 2 as LHS is equal to RHS, So 2 X 8 = 8 X 2.
2 × 10 = 10 × 2,
As each equation is true, so the missing factor in ___ X 2 is 10 as LHS is equal to RHS, So 2 X 10 = 10 X 2.
2 × 9 = 9 × 2,
As each equation is true, so the missing factor in 2 × ___ is 9 as LHS is equal to RHS, So 2 × 9 = 9 × 2.
Question 8.
Jada gets 2 new packs of erasers. Each pack has 6 erasers in it.
a. Draw an array to show how many erasers Jada has altogether.
b. Write and solve a multiplication sentence to describe the array.
c. Use the commutative property to write and solve a different multiplication sentence for the array.
Answer:
a.
Jada has 12 erasers altogether,
Explanation:
Given Jada gets 2 new packs of erasers. Each pack has 6 erasers in it.
So, drawn an array to show 2 × 6 = 12 number of erasers
Jada has altogether.
b. Multiplication sentence is 2 × 6 = 12, the array has 12 erasers.
Explanation:
Wrote and solved a multiplication sentence as 2 × 6 = 12 erasers, describing the array as 2 packs in rows and 6 erasers in columns, So 2 packs X 6 erasers = 12 erasers.
c. Commutative property for multiplication sentence for the array is 2 × 6 = 6 × 2 = 12.
Explanation:
Used the commutative property to write and solve a different multiplication sentence for the array as 2 × 6 = 6 x 2 = 12 erasers.
Eureka Math Grade 3 Module 1 Lesson 7 Exit Ticket Answer Key
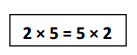
Do you agree or disagree with the statement in the box?
Draw arrays and use skip-counting to explain your thinking.
Answer:
Yes, I agree with the statement in the box as 2 x 5 = 5 X 2,
Explanation:
Yes, I agree or disagree with the statement in the box as 2 × 5 = 10 = 5 × 10,
Drawn arrays and used skip-counting as 2 × 5 = 10 = 5 × 10.
Eureka Math Grade 3 Module 1 Lesson 7 Homework Answer Key
Question 1.
a. Draw an array that shows 7 rows of 2.
b. Write a multiplication sentence where the first factor represents the number of rows.
____7____ × ___2____ = ____14____
Explanation:
Drawn an array that shows 7 rows of 2 as 7 × 2 as shown above in the picture.
b. Multiplication sentence where the first factor represents the number of rows as 7 × 2 = 14.
Explanation:
Wrote a multiplication sentence where the first factor represents the number of rows as 7 × 2 = 14.
Question 2.
a. Draw an array that shows 2 rows of 7.
b. Write a multiplication sentence where the first factor represents the number of rows.
____2____ × ___7_____ = ___14____

Explanation:
Drawn an array that shows 2 rows of 7 as 2 × 7 as shown above in the picture.
b. Multiplication sentence where the first factor represents the number of rows as 2 × 7 = 14.
Explanation:
Wrote a multiplication sentence where the first factor represents the number of rows as 2 × 7 = 14.
Question 3.
a. Turn your paper to look at the arrays in Problems 1 and 2 in different ways. What is the same and what is different about them?
b. Why are the factors in your multiplication sentences in a different order?
a. Same is the result because both have the same value as 14,
Different is number of rows and number of columns are not the same,
Explanation:
Turned my paper to look at the arrays in Problems 1 and 2 in different ways.
Is the same because both got same results as 14 and different about them is in problems 1 and 2 the number of rows and number of columns are not the same as one is 7 rows × 2 columns and in other it is 2 rows × 7 columns.
b. The factors in my multiplication sentences are in a different order because first we are taking 7 rows × 2 columns and in other it is 2 rows × 7 columns.
Explanation:
The factors in my multiplication sentences are in a different order because first we are taking 7 rows X 2 columns and in other it is 2 rows × 7 columns,
So, rows and columns differ in the both.
Question 4.
Write a multiplication sentence to match the number of groups.
Skip-count to find the totals. The first one is done for you.
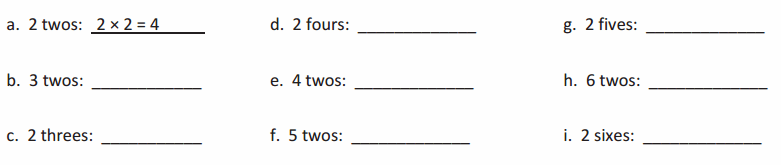
Explanation:
Wrote a multiplication sentence to match the number of groups as shown above, might have skipped-count to find the totals.
Question 5.
Write and solve multiplication sentences where the second factor represents the size of the row.
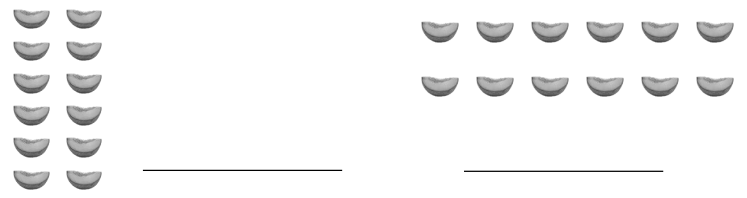

Explanation:
Wrote and solved multiplication sentences where the second factor represents the size of the row as
2 × 6 = 12 and 6 × 2= 12.
Question 6.
Angel writes 2 × 8 = 8 × 2 in his notebook.
Do you agree or disagree? Draw arrays to help explain your thinking.
Explanation:
Given Angel writes 2 × 8 = 8 × 2 in his notebook,
Yes, I agree because 2 × 8 = 16 and 8 x 2 = 16,
Drawn arrays to help and explained my thinking as shown above.
Question 7.
Find the missing factor to make each equation true.


Explanation:
Found the missing factor to make each equations true as below
2 × 6 = 6 × 2,
As each equation is true, so the missing factor in 6 × ___ is 2 as LHS is equal to RHS, So 2 × 6 = 6 × 2.
7 × 2 = 2 × 7,
As each equation is true, so the missing factor in ___ × 2 is 7 as LHS is equal to RHS, So 7 × 2 = 2 × 7.
9 × 2 = 2 × 9,
As each equation is true, so the missing factor in ___ × 9 is 2 as LHS is equal to RHS, So 9 × 2 = 2 × 9.
2 × 10 = 10 × 2,
As each equation is true, so the missing factor in 2 × ___ is 10 as LHS is equal to RHS, So 2 × 10 = 10 × 2.
Question 8.
Tamia buys 2 bags of candy.
Each bag has 7 pieces of candy in it.
a. Draw an array to show how many pieces of candy Tamia has altogether.
b. Write and solve a multiplication sentence to describe the array.
c. Use the commutative property to write and solve a different multiplication sentence for the array.
a.
Tamia has 14 candy’s altogether,
Explanation:
Given Tamia buys 2 bags of candy. Each bag has 7 pieces of candy in it.
So, drawn an array to show 2 × 7 = 14 number of candy’s Tamia has altogether.
b. Multiplication sentence is 2 × 7 = 14, the array has 14 candy’s.
Explanation:
Wrote and solved a multiplication sentence as 2 × 7 = 14 candy’s, describing the array as 2 bags in rows and 7 candy’s in columns, So 2 bags X 7 candy’s = 14 candy’s.
c. Commutative property for multiplication sentence for the array is 2 × 7 = 7 × 2 = 14.
Explanation:
Used the commutative property to write and solve a different multiplication sentence for the array as 2 × 7 = 7 x 2 = 14 candy’s.