Engage NY Eureka Math Geometry Module 2 Lesson 23 Answer Key
Eureka Math Geometry Module 2 Lesson 23 Example Answer Key
Example 1.
Explain how the expression 8. 3√2 + 7. 9√2 can be simplified using the distributive property.
Answer:
Each term of the expression has a common factor, √2. For that reason, the distributive property can be applied.
8. 3√2 + 7. 9√2 = (8.3 + 7. 9)√2 By the distributive property
= 16.2√2
Explain how the expression 11√7 – 6√7 + 3√2 can be simplified using the distributive property.
Answer:
The expression can be simplified because the first two terms contain the expression √7. Using the distributive property,
we get the following:
11√7 – 6√7 + 3√2 = (11 – 6)√7 + 3√2 By the distributive property
= 5√7 + 3√2
Example 2.
Explain how the expression 19√2 + 2√8 can be simplified using the distributive property.
Answer:
The expression can be simplified, but first the term 2√8 must be rewritten.
19√2 + 2√8 = 19√2 + 2√4 · √2 By Rule 1
= 19√2 + 2 · 2√2
= 19√2 + 4√2
= (19 + 4)√2 By the distributive property
= 23√2
Can the expression 19√2 + 2√8 be simplified using the distributive property?
Answer:
No, the expression cannot be simplified because neither term can be rewritten in a way that the distributive property could be applied.
Eureka Math Geometry Module 2 Lesson 23 Exercise Answer Key
Simplify each expression as much as possible.
Exercise 1.
√32 =
Answer:
√32 = √16√2
= 4√2
Exercise 2.
√45
Answer:
√45 = √9√5
= 3√5
Exercise 3.
√300 =
Answer:
√300 = √100√3
= 10√3
Exercise 4.
The triangle shown below has a perimeter of 6. 5√2 units. Make a conjecture about how this answer was reached.
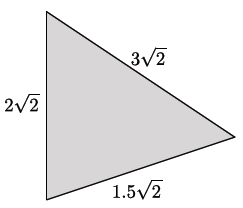
Answer:
It appears that when all three sides of the triangle were added, the numbers that preceded the square roots were the only numbers that were added:
3 + 2 + 1.5 = 6.5. The √2 shown as part of each length remained √2.
Exercise 5.
The sides of a triangle are 4√3, √12, and √75. Make a conjecture about how to determine the perimeter of this
triangle.
Answers will vary. The goal is for students to realize that √12 and √75 can be rewritten so that each has a factor of √3, which then strongly resembles Exercise 4. By rewriting each side length as a multiple of √3, we get Some students may answer incorrectly by adding 3 + 12 + 75. Show that this is incorrect using a simpler example.
√9 + √16 ≠ √25
Exercise 6.
Circle the expressions that can be simplified using the distributive property. Be prepared to explain your choices.
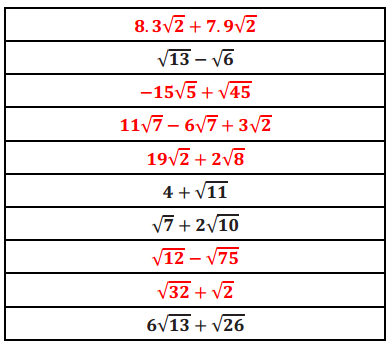
Answer:
The expressions that can be simplified using the distributive property are noted in red.
Eureka Math Geometry Module 2 Lesson 23 Problem Set Answer Key
Question 1.
18√5 – 12√5 =
Answer:
18√5 – 12√5 = (18 – 12)√5
= 6√5
Question 2.
√24 + 4√54 =
Answer:
= √24 + 4√54 = √4 · √6 + 4 · √9 · √6
= 2√6 + 4 · 3√6
= (2 + 12)√6
= 14√6
Question 3.
2√7 + 4√63 =
Answer:
2√7 + 4√63 = 2√7 + 4√9√7
= 2√7 + 4(3)√7
= (2 + 12)√7
= 14√7
Question 4.
What is the perimeter of the triangle shown below?

Answer:
2√2 + √12 + √32 = 2√2 + √4 · √3 + √16 · √2
= 2√2 + 2√3 + 4√2
= (2 + 4)√2 + 2√3
= 6√2 + 2√3
The perimeter of the triangle is 6√2 + 2√3 units.
Question 5.
Determine the area and perimeter of the triangle shown. Simplify as much as possible.
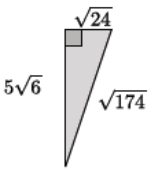
The perimeter of the triangle is
√24 + 5√6 + √174 = √4√6 + 5√6 + √174
= 2√6 + 5√6 + √174
= (2 + 5)√6 + √174
= 7√6 + √174.
The area of the triangle is
\(\frac{\sqrt{24}(5 \sqrt{6})}{2}=\frac{2 \sqrt{6}(5 \sqrt{6})}{2}=\frac{60}{2}\) = 30.
The perimeter is 7√6 + √174 units, and the area Is 30 square units.
Question 6.
Determine the area and perimeter of the rectangle shown. Simplify as much as possible.
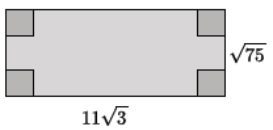
Answer:
The perimeter of the rectangle is
11√3 + 11√3 + √75 + √75 = 2(11√3) + 2(√25√3)
= 22√3 + 10√3
= (22 + 10)√3
= 32.
The area of the rectangle is
11√3(5√3) = 55(3)
= 165.
The perimeter is 32√3 units, and the area is 165 square units.
Question 7.
Determine the area and perimeter of the triangle shown. Simplify as much as possible.

Answer:
The perimeter of the triangle is
8√3 + 8√3 + √384 = (8 + 8)√3 + √384
= 16√3 + √384
= 16√3 + √64√6
= 16√3 + 8√6.
The area of the triangle is
\(\frac{(8 \sqrt{3})^{2}}{2}=\frac{8^{2}(\sqrt{3})^{2}}{2}\)
= \(\frac{64(3)}{2}\)
= 32(3)
= 96.
The perimeter of the triangle is 16√3 + 8√6 units, and the area of the triangle is 96 square units.
Question 8.
Determine the area and perimeter of the triangle shown. Simplify as much as possible.
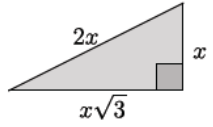
Answer:
The perimeter of the triangle is
2x + x + x√3 = 3x + x√3.
The area of the triangle is
\(\frac{x(x \sqrt{3})}{2}=\frac{x^{2} \sqrt{3}}{2}\)
The perimeter is 3x + x√3 units, and the area is \(\frac{x^{2} \sqrt{3}}{2}\) square units.
Question 9.
The area of the rectangle shown in the diagram below is 160 square units. Determine the area and perimeter of the shaded triangle. Write your answers in simplest radical form, and then approximate to the nearest tenth.
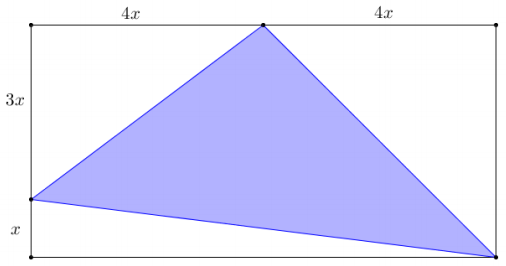
Answer:
The length of the rectangle is 8x, and the width is 4x. Using the given area of the rectangle:
Area = length × width
160 = 8x · 4x
160 = 32x2
5 = x2
Arearectangle = A1 + A2 + A3 + A4
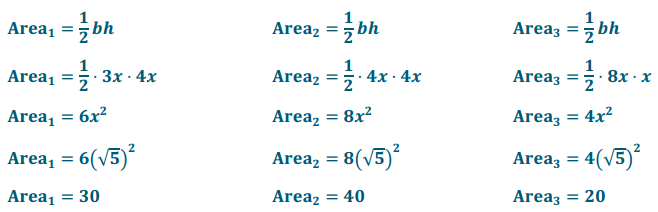
160 = 30 + 40 + 20 + A4
A4 = 70
The area of the shaded triangle in the diagram is 70 square units.
The perimeter of the shaded triangle requires use of the Pythagorean theorem to find the hypotenuses of right triangles 1,2, and 3. Let h1, h2, and h3 represent the lengths of the hypotenuses of triangles 1, 2, and 3, respectively.
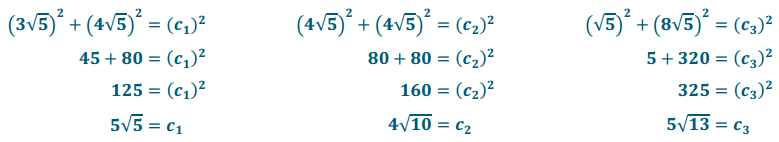
Perimeter = C1 + C2 + C3
Perimeter = 5√5 + 4√10 + 5√13
The perimeter of the shaded triangle is approximately 41.9 units.
Question 10.
Parallelogram ABCD has an area of 9 square units. DC = 3√3 and G and H are midpoints of \(\overline{D E}\) and \(\overline{C E}\), respectively. Find the area of the shaded region. Write your answer in simplest radical form.
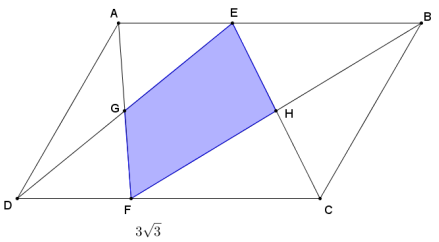
Answer:
Using the area of a parallelogram:
Area(ABCD) = bh
9√3 = 3√3 · h
3 = h
The height of the parallelogram is 3.
The area of the shaded region is the sum of the areas of ∆ EGH and ∆ FGH.
The given points G and H are midpoints of \(\overline{D E}\) and \(\overline{C E}\); therefore, by the triangle side splitter theorem, [/latex] and \(\overline{G H}\) must be parallel to [/latex] and \(\overline{D C}\), and thus, also parallel to [/latex] and \(\overline{A B}\). Furthermore,
GH = \(\frac{1}{2}\)CD = \(\frac{1}{2}\)AB = \(\frac{3}{2}\)√3.
∆ EGH ~ ∆ EDC by AA ~ criterion with a scale factor of \(\frac{1}{2}\). The areas of scale drawings are related by the square of the scale factor; therefore, Area(∆ EGH) = \(\left(\frac{1}{2}\right)^{2}\) Area(∆ EDC).

Eureka Math Geometry Module 2 Lesson 23 Exit Ticket Answer Key
Question 1.
Simplify 5√11 – 17√11.
Answer:
5√11 – 17√11 = (5 – 17)√11
= – 12√11
Question 2.
Simplify √8 + 5√2.
Answer:
√8 + 5√2 = √4√2 + 5√2
= 2√2 + 5√2
= (2 + 5)√2
= 7√2
Question 3.
Write a radical addition or subtraction problem that cannot be simplified, and explain why it cannot be simplified.
Answer:
Answers will vary. Students should state that their expression cannot be simplified because one or both terms cannot be rewritten so that each has a common factor. Therefore, the distributive property cannot be applied.