Engage NY Eureka Math Algebra 1 Module 3 Lesson 1 Answer Key
Eureka Math Algebra 1 Module 3 Lesson 1 Example Answer Key
Example 1.
Jerry has thought of a pattern that shows powers of two. Here are the first six numbers of Jerry’s sequence:
1, 2, 4, 8, 16, 32, ….
Write an expression for the nth number of Jerry’s sequence.
Answer:
The expression 2(n – 1) generates the sequence starting with n = 1.
Example 2.
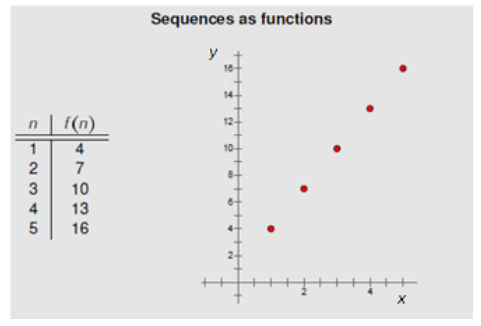
Consider the sequence that follows a plus 3 pattern: 4, 7, 10, 13, 16, ….
a. Write a formula for the sequence using both the a_n notation and the f(n) notation.
Answer:
an = 3n + 1 or f(n) = 3n + 1 starting with n = 1
b. Does the formula f(n) = 3(n – 1) + 4 generate the same sequence? Why might some people prefer this formula?
Answer:
Yes, 3(n – 1) + 4 = 3n – 3 + 4 = 3n + 1. It is nice that the first term of the sequence is a term in the formula, so one can almost read the formula in plain English: Since there is the “plus 3” pattern, the nth term is just the first term plus that many more threes.
c. Graph the terms of the sequence as ordered pairs (n,f(n)) on the coordinate plane. What do you notice about the graph?
The points all lie on the same line.
Answer:
The points all lie on the same line.
Eureka Math Algebra 1 Module 3 Lesson 1 Exercise Answer Key
Opening Exercise
Mrs. Rosenblatt gave her students what she thought was a very simple task:
What is the next number in the sequence 2, 4, 6, 8, …?
Cody: I am thinking of a plus 2 pattern, so it continues 10, 12, 14, 16, ….
Ali: I am thinking of a repeating pattern, so it continues 2, 4, 6, 8, 2, 4, 6, 8, ….
Suri: I am thinking of the units digits in the multiples of two, so it continues 2, 4, 6, 8, 0, 2, 4, 6, 8, ….
a. Are each of these valid responses?
Answer:
Each response must be considered valid because each one follows a pattern.
b. What is the hundredth number in the sequence in Cody’s scenario? Ali’s? Suri’s?
Answer:
Cody: 200 Ali: 8 Suri: 0
c. What is an expression in terms of n for the nth number in the sequence in Cody’s scenario?
Answer:
2n is one example. Note: Another student response might be 2(n + 1) if the student starts with n = 0 (see Example 1).
Exercises
Exercise 1.
Refer back to the sequence from the Opening Exercise. When Mrs. Rosenblatt was asked for the next number in the sequence 2, 4, 6, 8, …, she said “17.” The class responded, “17?”
Yes, using the formula f(n) = \(\frac{7}{24}\) (n – 1)4 – \(\frac{7}{4}\) (n – 1)3 + \(\frac{77}{24}\) (n – 1)2 + \(\frac{1}{4}\)(n – 1) + 2.
a. Does her formula actually produce the numbers 2, 4, 6, and 8?
Answer:
Yes. f(1) = 2, f(2) = 4, f(3) = 6, f(4) = 8
b. What is the 100th term in Mrs. Rosenblatt’s sequence?
Answer:
f(100) = 26 350 832
Exercise 2.
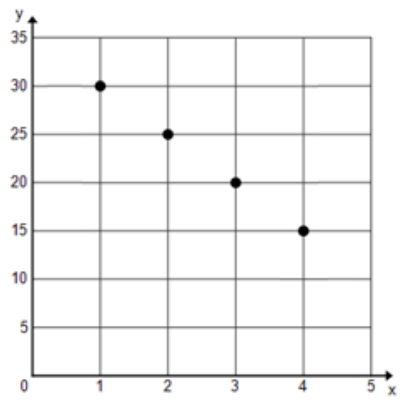
Consider a sequence that follows a minus 5 pattern: 30, 25, 20, 15, ….
a. Write a formula for the nth term of the sequence. Be sure to specify what value of n your formula starts with.
Answer:
f(n) = 35 – 5n starting with n = 1
b. Using the formula, find the 20th term of the sequence.
Answer:
– 65
c. Graph the terms of the sequence as ordered pairs (n,f(n)) on a coordinate plane.
Answer:
Exercise 3.
Consider a sequence that follows a times 5 pattern: 1, 5, 25, 125, ….
a. Write a formula for the nth term of the sequence. Be sure to specify what value of n your formula starts with.
Answer:
f(n) = 5n – 1 starting with n = 1
b. Using the formula, find the 10th term of the sequence.
Answer:
f(10) = 1 953 125
c. Graph the terms of the sequence as ordered pairs (n,f(n)) on a coordinate plane.
Answer:
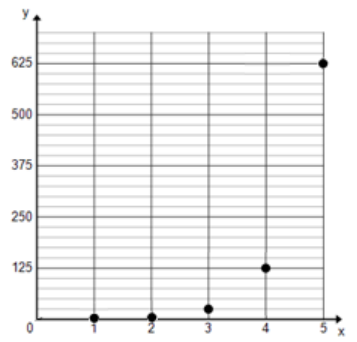
Exercise 4.
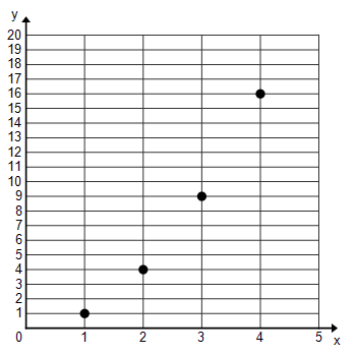
Consider the sequence formed by the square numbers:
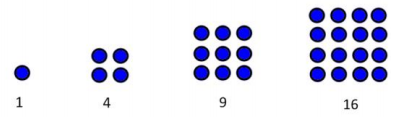
a. Write a formula for the nth term of the sequence. Be sure to specify what value of n your formula starts with.
Answer:
f(n) = n2 starting with n = 1
b. Using the formula, find the 50th term of the sequence.
Answer:
f(50) = 2500
c. Graph the terms of the sequence as ordered pairs (n,f(n)) on a coordinate plane.
Answer:
Exercise 5.
A standard letter – sized piece of paper has a length and width of 8.5 inches by 11 inches.
a. Find the area of one piece of paper.
Answer:
93.5 in2
b. If the paper were folded completely in half, what would be the area of the resulting rectangle?
Answer:
46.75 in2
c. Write a formula for a sequence to determine the area of the paper after n folds.
Answer:
f(n) = \(\frac{93.5}{2^{n}}\) starting with n = 1, or f(n) = \(\frac{93.5}{2^{n + 1}}\) starting with n = 0
d. What would the area be after 7 folds?
Answer:
0.73046875 in2
Eureka Math Algebra 1 Module 3 Lesson 1 Problem Set Answer Key
Question 1.
Consider a sequence generated by the formula f(n) = 6n – 4 starting with n = 1. Generate the terms f(1), f(2), f(3), f(4), and f(5).
Answer:
2, 8, 14, 20, 26
Question 2.
Consider a sequence given by the formula f(n) = \(\frac{1}{3^{n – 1}}\) starting with n = 1. Generate the first 5 terms of the sequence.
Answer:
1, \(\frac{1}{3}\), \(\frac{1}{9}\), \(\frac{1}{27}\), \(\frac{1}{81}\)
Question 3.
Consider a sequence given by the formula f(n) = ( – 1)n × 3 starting with n = 1. Generate the first 5 terms of the sequence.
Answer:
– 3, 3, – 3, 3, – 3
Question 4.
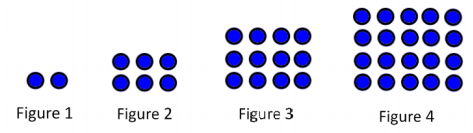
Here is the classic puzzle that shows that patterns need not hold true. What are the numbers counting?
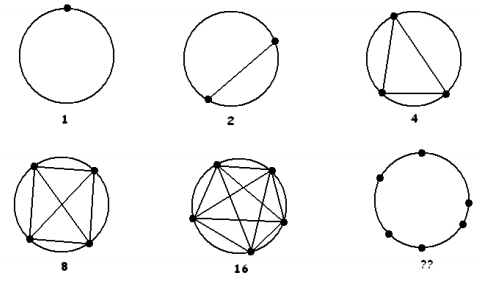
Answer:
The number under each figure is counting the number of (non – overlapping) regions in the circle formed by all the segments connecting all the points on the circle. Each graph contains one more point on the circle than the previous graph.
a. Based on the sequence of numbers, predict the next number.
Answer:
32
b. Write a formula based on the perceived pattern.
Answer:
f(n) = 2(n – 1) starting with n = 1
c. Find the next number in the sequence by actually counting.
Answer:
31 (Depending on how students draw the segments, it is also possible to get 30 as the next number in the sequence, but it is definitely NOT 32.)
d. Based on your answer from part (c), is your model from part (b) effective for this puzzle?
Answer:
No. It works for n = 1 to n = 5 but not for n = 6. And we do not know what happens for values of n larger than 6.
For each of the sequences in Problems 5–8:
a. Write a formula for the nth term of the sequence. Be sure to specify what value of n your formula starts with.
b. Using the formula, find the 15th term of the sequence.
c. Graph the terms of the sequence as ordered pairs (n,f(n)) on a coordinate plane.
Question 5.
The sequence follows a plus 2 pattern: 3, 5, 7, 9, ….
Answer:
a. f(n) = 2(n – 1) + 3 starting with n = 1
b. f(15) = 31
c.
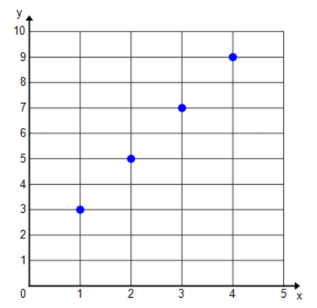
Question 6.
The sequence follows a times 4 pattern: 1, 4, 16, 64, ….
Answer:
a. f(n) = 4(n – 1) starting with n = 1
b. f(15) = 268 435 456
c.

Question 7.
The sequence follows a times – 1 pattern: 6, – 6, 6, – 6, ….
Answer:
a. f(n) = ( – 1)(n – 1) ⋅ 6 starting with n = 1
b. f(15) = 6
c.
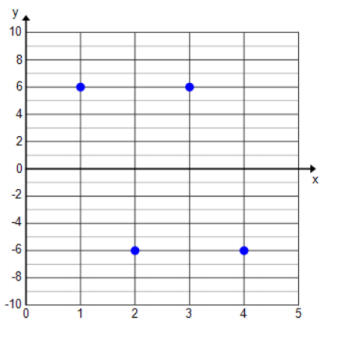
Question 8.
The sequence follows a minus 3 pattern: 12, 9, 6, 3, ….
Answer:
a. f(n) = 12 – 3(n – 1) starting with n = 1
b. f(15) = – 30
c.
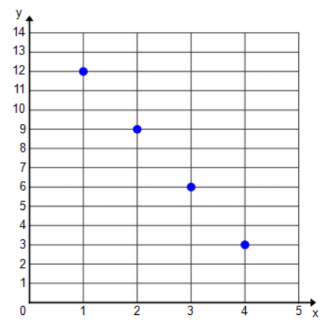
Eureka Math Algebra 1 Module 3 Lesson 1 Exit Ticket Answer Key
Question 1.
Consider the sequence given by a plus 8 pattern: 2, 10, 18, 26, ….
Shae says that the formula for the sequence is f(n) = 8n + 2. Marcus tells Shae that she is wrong because the formula for the sequence is f(n) = 8n – 6.
a. Which formula generates the sequence by starting at n = 1? At n = 0?
Answer:
Shae’s formula generates the sequence by starting with n = 0, while Marcus’s formula generates the sequence by starting with n = 1.
b. Find the 100th term in the sequence.
Answer:
Using Marcus’s formula: f(100) = 8(100) – 6 = 794
Using Shae’s formula: f(99) = 8(99) + 2 = 794
Question 2.
Write a formula for the sequence of cube numbers: 1, 8, 27, 64, ….
Answer:
f(n) = n3 starting with n = 1