Find a Collection of Worksheets Involving Prime Factorization Methods and use them as a part of your reference. Prime Factorization Worksheet available has questions on finding the prime factors of a number using division method, factor tree method, and many more. Activity Worksheet on Prime Factorization Methods will support your child’s learning and help them understand how it works as well as ideas on how to solve related problems easily. Practice the Questions in Prime Factorization Worksheet and understand the concept well.
Do Refer:
Prime Factorization Worksheets with Answers
Problem 1.
Find the Prime factors of 124 using the Division Method?
Solution:
Firstly, divide the number 124 with the least prime number i.e. 2
124÷2 = 62
take the quotient and divide the number again with the least prime number
62÷2 = 31
Since 31 is a prime number that has factors 1 and itself we can’t proceed further.
Therefore, Prime Factors of 124 are 2, 2, 31 and it can be written in prime factorization method as 2*2*31.
Problem 2.
Determine the Prime Factorization for Number 56 by any Method of your Choice?
Solution:
Let us find the prime factorization for number 56 using the factor tree method. Write down 56 as the root of the tree and find the factors of it.
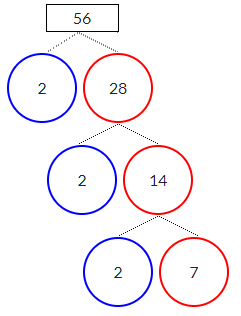
We get the factors of 56 as 2 and 28 in the initial step. We can further continue the process and get the factor pairs of 28 and write them in the branches. Repeat the process till you get all prime numbers at the end.
Therefore, Prime Factors of Number 56 using the Factor Tree Method is 2, 2, 2, 7
Expressing it in prime factorization we have 2*2*2*7.
Problem 3:
Following is the prime factorization of a particular number. Find the numbers.
(i) 2 × 5 × 5
(ii) 2 × 5 × 11
(iii) 2 × 3 × 5
Solution:
From the definition of prime factorization, we know it is the process of writing the given number as a product of prime numbers. Thus, on multiplying the prime factors we will get the original number.
(i) 2 × 5 × 5
= 50
(ii) 2 × 5 × 11
= 110
(iii) 2 × 3 × 5
=30
Problem 4.
Write down the prime factors of the number 33 using Prime Decomposition or Factor Tree?
Solution:
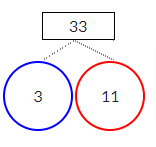
Write down the number 33 as the root of the tree. Then check the factors of the number.
33 can be written in factors as 3*11
As the numbers 3, 11 are prime the process no longer continues.
Prime Factors of 33 are 3, 11.
Problem 5:
Find the Prime Factors of 94 using the Trial Division Method?
Solution:
Divide the number 94 with the least prime number i.e. 2
94÷2 = 47
Since the quotient is a prime number we no longer do the division process anymore.
Prime Factors of 94 are 2, 47
Problem 6:
Following are the prime factors for a certain number. Find the numbers?
(i) 5 × 3 × 7
(ii) 2 × 3 × 7
(iii) 2 × 5 × 3 × 7
(iv) 2 × 5 × 2 × 7
Solution:
As per the definition of prime factorization, it is the product of prime numbers. Thus, we can simply multiply the prime numbers given to determine the original number.
(i) 5 × 3 × 7
= 105
(ii) 2 × 3 × 7
= 42
(iii) 2 × 5 × 3 × 7
= 210
(iv) 2 × 5 × 2 × 7
=140
Problem 7.
Find the Prime Factors of Number 85 using the Factor Tree Method?
Solution:
Note down the given number as the root of the number. Find the factors of the given number and note them. Since 85 has both the factors 5 and 17 as prime numbers we need not find the factor pairs again. That’s the end of the process.
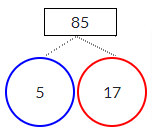
Prime factors of 85 are 5, 17.
Problem 8.
Find the Prime Factorization of number 136?
Solution:
Let us divide the number 136 using the least prime number i.e. 2
136÷2 =68
Take the quotient and divide it with the least prime number again.
68÷2=34
Take the quotient and divide it with the least prime number.
34÷2=17
Since 17 is a prime number the division process ends here.
Prime Factors of 136 are 2, 2, 2, 17.
