The equation of a straight line represents each and every point on that line. Let us consider the straight line created by passing through the two points such as (a1, b1) and (a2, b2). There are no curves present in the straight line. The basic equation for the straight line in Two-point for is ax + by + c = 0. Here, a, b, c are constants, and x and y are variables.
How to find the Equation of a Straight Line Passing Through Two Points?
The below diagram shows the straight line in two-point form. In this, (a1, b1) is the starting point of the straight line, and (a2, b2) is the ending point of the straight line.
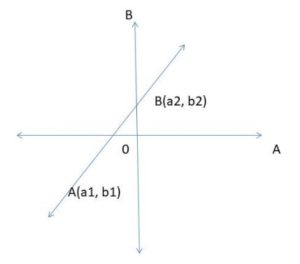
The equation of the straight line which is passing through the two points A(a1, b1) and B(a2, b2) is b – b1 = (b2 – b1) / (a2 – a1) * (a – a1). P(a, b)is the joining point of A and B.
The straight line is passing through the two points A and B. Then the slope of the line AB = (b1 – b2) / (a1- a2).———( 1 ).
Now, the straight line is passing through the two – points A and P. Then the slope of the line AP = (b – b1) / (a – a1). ——- ( 2 ).
To find out the equation of a straight line with two point form, we need to equate the two equations. That is,
Slope of the line AP = Slope of the line AB.
(b – b1) / (a – a1) = (b1 – b2) / (a1 – a2).
(b – b1) = (b1 – b2) / (a1 – a2) * (a – a1).
Equation for the straight line of two – point form is equal to (b – b1) = (b1 – b2) / (a1 – a2) * (a – a1).
Let us consider the slope (b1 – b2) / (a1 – a2) as ‘m’. substitute the value in the above equation. Then straight line equation becomes as
(b – b1) = m(a – a1).
Steps to Solve Equation of the Straight Line Problems
Follow the three steps to find the Equation of the Straight Line. They are
1. Find the slope of the line.
2. Put the slope and one point into the “Point-Slope Formula”.
3. Simplify the equation.
Also, See:
Two – Point Form Examples with Solutions
1. Find the Equation of the straight line passing through the points (1, 2), and (3, -2)?
Solution:
The given details are (a1, b1) = (1, 2) and (a2, b2) = (3, -2).
The equation for the straight line is (b – b1) = (b1 – b2) / (a1 – a2) * (a – a1).
Substitute the values in the above equation, then we will get
(b – 2) = (2 – (-2)) / (1 – 3) * (a – 1).
(b – 2) = (2 + 2) / (-2) * (a – 1).
(b – 2) = 4 / (-2) * (a – 1).
(b – 2) = -2 * ( a – 1).
b – 2 = -2a + 1.
2a + b – 2 -1 = 0.
2a + b – 3 = 0.
Finally the straight line equation is 2a + b – 3 = 0.
2. Find the equation of the straight line joining the points (-2, 4) and (5, 6)?
Solution:
As per the given information, the straight line is created by joining the two – points. They are (a1, b1) = (-2, 4) and (a2, b2) = (5, 6).
Equation for the straight line of joining two points is (b – b1) = (b1 – b2) / (a1 – a2) * (a – a1).
Substitute the values in the above equation, then we will get like
(b – 4) = (4 – 6) / (-2 – 5) * (a – (-2)).
(b – 4) = (- 2 / – 7) *(a + 2).
(b –4) (7) = 2 * (a + 2).
7b – 28 = 2a + 4.
-2a + 7b – 28 – 4 = 0.
-2a + 7b -32 = 0.
Therefore, the final equation for the straight line is -2a +7b – 32 = 0.
3. Find the straight-line equation with the help of two points (6, 2) and (8, 4)?
Solution:
The given information is the straight line is crossing the two points. They are (a1, b1) = (6, 2) and (a2, b2) = (8, 4).
The equation for the straight line in Two – point form is (b – b1) = (b1 – b2) / (a1 – a2) * (a – a1).
Substitute the values in the above equation, we will get
(b – 2) = (2 – 4) / ( 6 – 8) * ( a – 6).
(b – 2) = ( – 2) / ( – 2) * (a – 6).
(b – 2) = (a – 6).
-a + b – 2 + 6 = 0.
-a + b + 4 = 0.
a – b – 4 = 0.
Finally, the equation for the straight line in two – points is equal to a – b – 4 = 0.
4. Find the equation of a straight line that is passing through points A(6, 6) and B(10, 4)?
Solution:
As per the given information, the straight line is passing through the two points. They are
(a1, b1) = (6, 6) and (a2, b2) = (10, 4).
The basic equation for the straight line in two – point form is (b – b1) = (b1 – b2) / (a1 – a2) * (a – a1).
Substitute the above values in the equation. Then we will get like
(b – 6) = (6 – 4) / (6 – 10) * (a – 6).
(b – 6) = 2 / (-4) * (a – 6).
(b – 6) = 1 / (-2) * (a – 6).
-2 ( b – 6) = a – 6.
-2b + 12 = a – 6.
-a – 2b + 12 + 6 = 0.
a + 2b – 18 = 0.
Finally the equation for the straight line is a + 2b – 18 = 0.
5. Find the values of a for which the points A(a, -2), B(4, 2) and C(8, 10) are collinear?
Solution:
As per the given information, the given points A(a, -2), B(4, 2), and C(8, 10) are collinear.
(a, b) = (a, -2), (a1, b1) = (4, 2), and (a2, b2) = (8, 10)
So, the slope of the AB = slope of the BC.
(b1 – b) / (a1 – a) = (b2 – b1) / (a2 – a1).
Substitute the values in the above equation. Then we will get
(2 – (-2)) / ( 4 – a) = (10 – 2) / (8 – 4).
(2 + 2) / (4 – a) = 8 / 4.
4 / (4 – a) = 2.
4 = 2(4 – a).
4 – a = 2.
4 – 2 = a.
a = 2.
Finally, a is equal to 2.