Worried about how to find the Arc Length? Don’t Panic as we will guide you completely in this and help you with the definition of Arc Length, Formula and Proof for Length of the Arc explained in detail. Check out the step by step explanation provided for determining the Arc Length. Also, refer to the solved examples for calculating the length of the arc and solve related problems in no time.
In general, Arc Length is nothing but the distance along the curved line making the arc. Remember that Arc Length is greater than the Straight Line Distance present between the Endpoints. Know about Denotations in the Arc Length Formula in the later sections.
Prove that the radian measure of any angle at the centre of a circle is equal to the ratio of the arc subtending that angle at the centre to the radius of the circle?
Let, us consider XOY to be a given angle. Now, with Centre O and any radius \(\overline {O L} \) draw a circle. Consider the circle drawn intersects \(\overline {O X} \) and \(\overline {O Y} \) at Points L and M respectively.
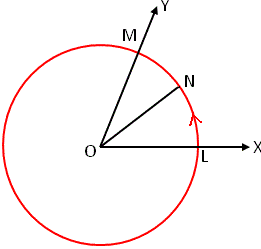
From the figure, it is clear that Arc LM subtends ∠LOM at Centre O. Now, take an Arc LN of length equal to the radius of the circle and join \(\overline {O N} \).
From definition, ∠LON = 1 radian.
We know the ratio of two arcs in a circle is equal to the ratio of the angles subtended by the arcs at the center of the circle,
Therefore, ∠LOM/∠LON = Arc LM/Arc LN
or, ∠LOM/1 radian = Arc LM/Radius \(\overline {O L} \)
or, ∠LOM = Arc LM/Radius OL × 1 radian = Arc LM/ Radius \(\overline {O L} \) radian.
Thus, circular measures of ∠LOM is Arc LM/Radius \(\overline {O L} \)
Let us consider θ be the circular measure of ∠LOM, Arc LM = s and Radius of the circle = \(\overline {O L} \) = r then,
θ = s/r, [i.e. theta equals s over r]
or, s = r θ, [i.e. s r theta formula]
Denotations in the Arc Length Formula
- s is the Arc Length
- r is the Radius of the Circle
- θ is the Central Angle of the Arc
Formulas to Measure the Arc Length
| Arc Length Formula (if θ is in degrees) | s = 2 π r (θ/360°) |
| Arc Length Formula in Integral Form | s=\(\int^{b}_a\sqrt{1+(\frac{dy}{dx})^2}dx\) |
| Arc Length Formula (if θ is in radians) | s = θ × r |
Solved Examples on Arc Length using the Formula s = rθ
1. Calculate the Length of the Arc if the radius of the circle is 9 cm and θ = 45°?
Solution:
We know the formula to Calculate the Arc Length s = rθ
Substituting the given input values r = 9 cm, θ =45° we get
Arc Length = 9*45°
= 9*0.785398(since 45° in radians =0.785398)
= 7.06 cm
Therefore, Arc Length is 7.06 cm
2. What would be the length of the arc formed by 65° of a circle having a diameter of 14 cm?
Solution:
From the given data
θ =65°
Diameter of the Circle = 14 cm
Radius of the Circle = \(\frac { d }{ 2 } \)
= \(\frac { 14 }{ 2 } \)
= 7 cm
We know the formula to calculate the Arc Length s = rθ
= 7*65°
= 7*1.13446
= 7.94 cm
Therefore, Arc Length is 7.94cm