Are you in a dilemma on the concept of Pure Recurring Decimals? If so, you will get a complete grip on Pure Recurring Decimals such as Definition, Examples, Procedure on How to Identify a Pure Recurring Decimal. Furthermore, refer to the solved examples on Pure Recurring Decimals for a better idea of the concept.
Also, Read:
Pure Recurring Decimal – Definition
A Decimal in which all the digits in the decimal part are repeated is called a Pure Recurring Decimal.
For Example: When 5/3 is divided the quotient is 1.6666…. and all the digits in the decimal part repeat continuously it is called a Pure Recurring Decimal.
How to Identify a Pure Recurring Decimal?
Follow the simple guidelines on how to identify a pure recurring decimal. They are in the following fashion
- Firstly, divide the numerator with the denominator from the given fraction.
- After dividing if you get to see all the digits in the decimal part repeat infinitely then it is called a pure recurring decimal.
For a better understanding of the concept of Pure Recurring Decimals check out few worked-out examples provided in the later sections.
Pure Recurring Decimal Examples
1. Is \(\frac { 5 }{ 3 } \) a Pure Recurring Decimal?
Solution:
Simply divide the numerator 5 with denominator 3. Check for if all the digits in the decimal part repeat or not after performing the division process. Simply place a bar on the repeating digits itself.
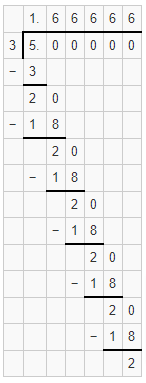
\(\frac { 5 }{ 3 } \) = 1.66666……
Thus, \(\frac { 5 }{ 3 } \) expressed in decimal form is 1.6666…. or 1.\(\overline{6}\)
1.6666…. is called a Pure Recurring Decimal as it has all the digits after the decimal part repeating.
2. Is \(\frac { 7 }{ 3 } \) a Pure Recurring Decimal?
Solution:
Simply divide the numerator 7 with denominator 3. Check for if all the digits in the decimal part repeat or not after performing the division process. Simply place a bar on the repeating digits itself.

\(\frac { 7 }{ 3 } \) = 2.333333……
Thus, \(\frac { 7 }{ 3 } \) expressed in decimal form is 2.3333…. or 2.\(\overline{3}\)
2.3333…. is called a Pure Recurring Decimal as it has all the digits after the decimal part repeating.
FAQs on Pure Recurring Decimals
1. What is a Pure Recurring Decimal?
A Decimal in which all the digits after the decimal point repeat is called a Pure Recurring Decimal.
2. How to Determine a Pure Recurring Decimal?
Just divide the numerator with the denominator and check if all the digits of the decimal part repeat or not. If the digits repeat then it is said to be a pure recurring decimal.
3. Is 1/3 a Pure Recurring Decimal?
Yes, 1/3 expressed in decimal form is 0.3333…. as it has all the digits in the decimal part repeat continuously.
