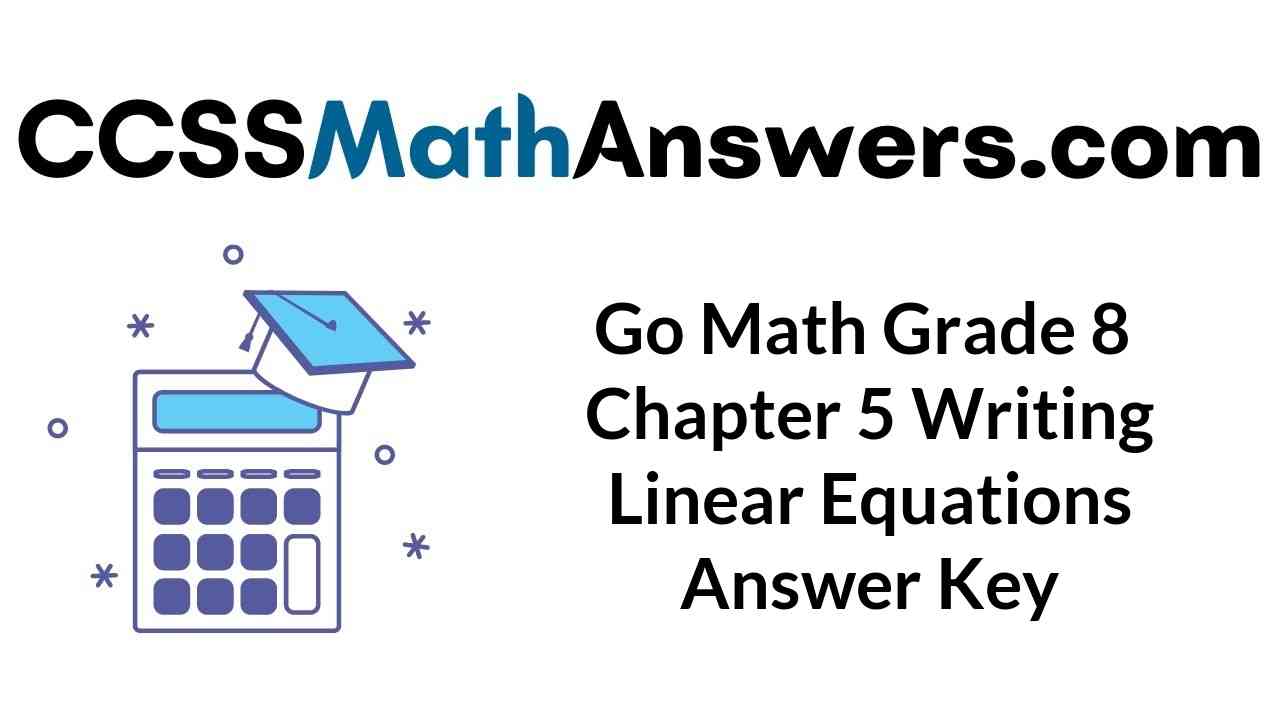It is essential for the students to have the best material to study for the exams. Go Math Grade 8 Answer Key Chapter 5 Writing Linear Equations recommend to every student who wants to succeed in math. Fall in love with math by practicing the problems from Go Math 8th Grade Chapter 5 Writing Linear Equations Solution Key. We have provided the step by step explanation for each and every question in CCSS Math Answers. Quick & smart learning is possible with the Go Math Grade 8 Answer Key Chapter 5 Writing Linear EquationsPDF.
Go Math Grade 8 Chapter 5 Writing Linear Equations Answer Key
The students who are willing to become masters in maths are suggested to follow our Go Math 8th Grade Chapter 5 Writing Linear Equations Solution Key. You can get free access for Go Math Grade 8 Answer Key Chapter 5 Writing Linear equations topicwise here. Check out the topics of Writing Linear equations from the below section.
Lesson 1: Writing Linear Equations from Situations and Graphs
- · Writing Linear Equations from Situations and Graphs – Page No. 130
- · Writing Linear Equations from Situations and Graphs – Page No. 131
- · Writing Linear Equations from Situations and Graphs – Page No. 132
Lesson 2: Writing Linear Equations from a Table
- · Writing Linear Equations from a Table – Page No. 136
- · Writing Linear Equations from a Table – Page No. 137
- · Writing Linear Equations from a Table – Page No. 138
Lesson 3: Linear Relationships and Bivariate Data
- · Linear Relationships and Bivariate Data – Page No. 144
- · Linear Relationships and Bivariate Data – Page No. 145
- · Linear Relationships and Bivariate Data – Page No. 146
Model Quiz
Mixed Review
Guided Practice – Writing Linear Equations from Situations and Graphs – Page No. 130
Question 1.
Li is making beaded necklaces. For each necklace, she uses 27 spacers, plus 5 beads per inch of necklace length. Write an equation to find how many beads Li needs for each necklace.
a. input variable:
____________
Answer:
The length of the necklace in inches
Question 1.
b. output variable:
____________
Answer:
The total number of beads in the necklace
Question 1.
c. equation:
Type below:
____________
Answer:
y = 5x
Question 2.
Kate is planning a trip to the beach. She estimates her average speed to graph her expected progress on the trip. Write an equation in slope-intercept form that represents the situation.
Type below:
____________
Answer:
y = -60x + 300
Explanation:
Choose two points on the graph to find the slope.
Find the slope
m = (y2 -y1)/(x2 – x1)
m = -300/5 = -60
Read the y-intercept from the graph: b = 300
Use your slope and y-intercept values to write an equation in slope-intercept
form.
y = -60x + 300
Question 3.
At 59 °F, crickets chirp at a rate of 76 times per minute, and at 65 °F, they chirp 100 times per minute. Write an equation in slope-intercept form that represents the situation.
Type below:
____________
Answer:
y = 4x – 160
Explanation:
Input variable: Temperature
Output variable: Number of chirps per minute
Slope:
m = (y2 -y1)/(x2 – x1) = (100 – 76)/(65 – 59) = 24/6 = 4
100 = 4(65) + b
y-intercept:
b = -160
Substituting the value of the slope m and y-intercept in the slope-intercept form. y = mx + b where, m = 4 and b = -160.
y = 4x – 160
Essential Question Check-In
Question 4.
Explain what m and b in the equation y = mx + b tell you about the graph of the line with that equation.
Type below:
____________
Answer:
The equation of any straight line, called a linear equation, can be written as: y = mx + b, where m is the slope of the line and b is the y-intercept.
m = change in y-value/change in x-value
The y-intercept of this line is the value of y at the point where the line crosses the y-axis.
Independent Practice – Writing Linear Equations from Situations and Graphs – Page No. 131
Question 5.
A dragonfly can beat its wings 30 times per second. Write an equation in slope-intercept form that shows the relationship between flying time in seconds and the number of times the dragonfly beats its wings
Type below:
____________
Answer:
y = 30x
Explanation:
The linear equation is y = mx + b where m is the slope and b is the y-intercept.
y variable will be the number of times the dragonfly has beat its wings and the x variable will be the time.
A dragonfly can beat its wings 30 times per second.
To find b, let’s consider how many times the dragonfly has beat its wings at time 0s.
So, the equation of the line is y = 30x
Question 6.
A balloon is released from the top of a platform that is 50 meters tall. The balloon rises at the rate of 4 meters per second. Write an equation in slope-intercept form that tells the height of the balloon above the ground after a given number of seconds.
Type below:
____________
Answer:
y = 4x + 50
Explanation:
Input variable: Number of seconds
Output variable: Height of the balloon
The balloon rises at a rate of 4 meters per second. m = 4;
A balloon is released from the top of a platform that is 50 meters tall. b = 50.
y = 4x + 50
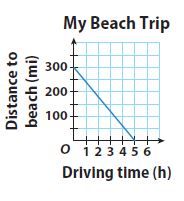
The graph shows a scuba diver’s ascent over time.
Question 7.
Use the graph to find the slope of the line. Tell what the slope means in this context.
Slope = _______ meters per second
Answer:
Slope = 1/8 or 0.125 meters per second
Explanation:
10m/80sec = 1/8
The scuba diver’s ascent gives up 1 meter per 16 seconds.
Question 8.
Identify the y-intercept. Tell what the y-intercept means in this context.
y-intercept = _______ meters
Answer:
y-intercept = -10 meters
Explanation:
The scuba divers start 10 meters below the water surface
Question 9.
Write an equation in slope-intercept form that represents the diver’s depth over time.
Type below:
____________
Answer:
y = 1/8 x – 10
Question 10.
The formula for converting Celsius temperatures to Fahrenheit temperatures is a linear equation. Water freezes at 0°C, or 32°F, and it boils at 100°C, or 212°F. Find the slope and y-intercept for a graph that gives degrees Celsius on the horizontal axis and degrees Fahrenheit on the vertical axis. Then write an equation in slope-intercept form that converts degrees Celsius into degrees Fahrenheit.
Type below:
____________
Answer:
Input variable: Celsius
Output variable: Fahrenheit
(0, 32) (100, 212)
m = (y2 -y1)/(x2 – x1) = (212 – 32)/(100 – 0) = 180/100 = 1.8
y intercepts = 32 when x = 0
F = 1.8C + 32
Question 11.
The cost of renting a sailboat at a lake is $20 per hour plus $12 for lifejackets. Write an equation in slope-intercept form that can be used to calculate the total amount you would pay for using this sailboat.
Type below:
____________
Answer:
y = 20x + 12
Explanation:
Input variable: Number of hours sailboat is rented
Output variable: Total cost
The cost of renting a sailboat at a lake is $20 per hour plus $12 for lifejackets.
Slope m = 20; y-intercept b = 12
Substituting the value of the slope m and y-intercept in the slope-intercept form. y = mx + b where, m = 20 and b = 12.
y = 20x + 12
Writing Linear Equations from Situations and Graphs – Page No. 132
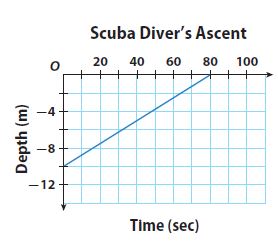
The graph shows the activity in a savings account.
Question 12.
What was the amount of the initial deposit that started this savings account?
$ _______
Answer:
$1000
Explanation:
The amount of the initial deposit that started this savings account is $1000
Question 13.
Find the slope and y-intercept of the graphed line.
Type below:
____________
Answer:
slope = 500
y-intercept = 1000
Explanation:
slope m = (y2 -y1)/(x2 – x1) = (2000 – 1500)/(2 – 1) = 500/1 = 500
y-intercept = 1000
Question 14.
Write an equation in slope-intercept form for the activity in this savings account.
Type below:
____________
Answer:
y = 500x + 1000
Explanation:
Substituting the value of the slope m and y-intercept in the slope-intercept form. y = mx + b where, m = 500 and b = 1000.
y = 500x + 1000
Question 15.
Explain the meaning of the slope in this graph.
Type below:
____________
Answer:
The slope represents the amount of money saved in dollars per month in the plan.
H.O.T.
Focus on Higher Order Thinking
Question 16.
Communicate Mathematical Ideas
Explain how you decide which part of a problem will be represented by the variable x, and which part will be represented by the variable y in a graph of the situation.
Type below:
____________
Answer:
y=mx+b
M-slope
B-Y intercept
and
(x,y)- would be any point on the graph and if you were to plug those points in for x and y the equation would solve if done properly
Question 17.
Represent Real-World Problems
Describe what would be true about the rate of change in a situation that could not be represented by a graphed line and an equation in the form y = mx + b.
Type below:
____________
Answer:
The rate of change would not be constant. Using different pairs of points in the slope formula would give different results.
Question 18.
Draw Conclusions
Must m, in the equation y = mx + b, always be a positive number? Explain.
Type below:
____________
Answer:
No; The slope m can be negative or positive. If the slope of the number is positive (the graph goes upward from left to right), then m will be positive, but if the slope is negative (the graph goes down from left to right), then m is negative.
Guided Practice – Writing Linear Equations from a Table – Page No. 136
Question 1.
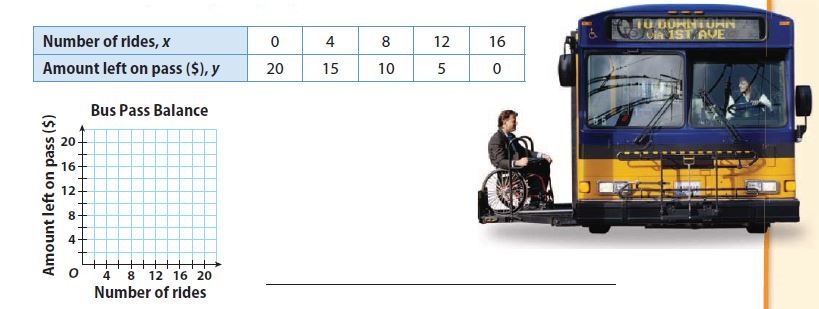
Jaime purchased a $20 bus pass. Each time he rides the bus, a certain amount is deducted from the pass. The table shows the amount, y, left on his pass after x rides. Graph the data, and find the slope and y-intercept from the graph or from the table. Then write the equation for the graph in slope-intercept form.
Type below:
____________
Answer:
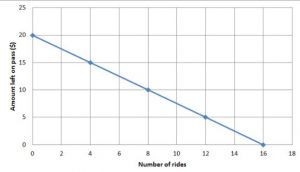
y = -5/4 x + 20
Explanation:
Slope = -20/16 = -5/4 = -1.25
y- intercepts = 20
Substituting the value of the slope m and y-intercept in the slope-intercept form. y = mx + b where, m = -1.25 and b = 20.
y = -5/4 x + 20
The table shows the temperature (y) at different altitudes (x). This is a linear relationship.

Question 2.
Find the slope for this relationship.
_______
Answer:
Slope m = (y2 -y1)/(x2 – x1) = (51 – 59)/(2000 – 0) = -8/2000 = -0.004
Explanation:
(x1, y1) = (0, 59), (x2, y2) = (2000, 51)
Slope m = (y2 -y1)/(x2 – x1) = (51 – 59)/(2000 – 0) = -8/2000 = -0.004
Question 3.
Find the y-intercept for this relationship.
y-intercept = _______
Answer:
b = 50
Explanation:
y-intercept = 59 when x = 0
Question 4.
Write an equation in slope-intercept form that represents this relationship.
Type below:
____________
Answer:
y = -0.004x + 59
Explanation:
Substituting the value of the slope m and y-intercept in the slope-intercept form. y = mx + b where, m = -0.004 and b = 59.
Question 5.
Use your equation to determine the temperature at an altitude of 5000 feet.
_______ °F
Answer:
39°F
Explanation:
y = -0.004x + 59
y = -0.004(5000) + 59 = -20 + 59 = 39
The temperature is 39°F at the altitude of 5000 feet.
Essential Question Check-In
Question 6.
Describe how you can use the information in a table showing a linear relationship to find the slope and y-intercept for the equation.
Type below:
____________
Answer:
Use any two points from the table to fins teh slope.
Slope m = (y2 -y1)/(x2 – x1)
If the value of y-intercept, when x=0 is not given in the table, use the slope and any ordered pair from the table and substitute in slope-intercept from y=mx + b to find b.
Independent Practice – Writing Linear Equations from a Table – Page No. 137
Question 7.
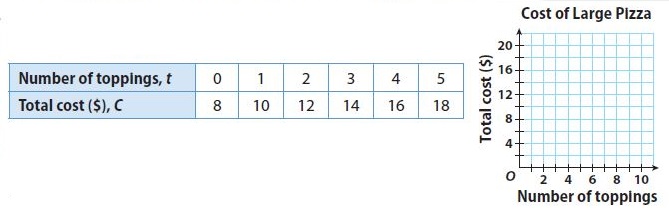
The table shows the costs of a large cheese pizza with toppings at a local pizzeria. Graph the data, and find the slope and y-intercept from the graph. Then write the equation for the graph in slope-intercept form.
Type below:
____________
Answer:
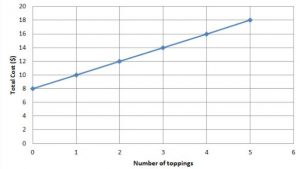
Slope m = (y2 -y1)/(x2 – x1) = (10 – 8)/(1 – 0) = 2/1 = 2
y-intercept b = 8
Substituting the value of the slope m and y-intercept in the slope-intercept form. y = mx + b where, m = 2 and b = 8.
y = 2x + 8
Question 8.
The table shows how much an air-conditioning repair company charges for different numbers of hours of work. Graph the data, and find the slope and y-intercept from the graph. Then write the equation for the graph in slope-intercept form.

Type below:
____________
Answer:
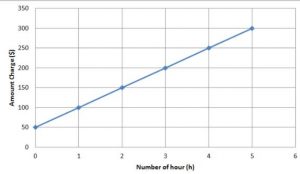
Slope m = (y2 -y1)/(x2 – x1) = (100 – 50)/(1 – 0) = 50/1 = 50
y-intercept b = 50
Substituting the value of the slope m and y-intercept in the slope-intercept form. y = mx + b where, m = 50 and b = 50.
y = 50x + 50
Question 9.
A friend gave Ms. Morris a gift card for a local car wash. The table shows the linear relationship of how the value left on the card relates to the number of car washes.
a. Write an equation that shows the number of dollars left on the card.

Type below:
____________
Answer:
y = -1.50x + 30
Explanation:
Slope m = (y2 -y1)/(x2 – x1) = (18 – 30)/(8 – 0) = -12/8 = -1.5
y-intercept b = 30
Substituting the value of the slope m and y-intercept in the slope-intercept form. y = mx + b where, m = -1.50 and b = 30.
y = -1.50x + 30
Question 9.
b. Explain the meaning of the negative slope in this situation.
Type below:
____________
Answer:
The negative slope means that the amount on the card decreased by $1.5 per car wash
Question 9.
c. What is the maximum value of x that makes sense in this context? Explain.
x = _______
Answer:
x = 20
Explanation:
0 = -1.50x + 30
1.5x = 30
x = 30/1.5 = 20
the maximum value of x = 20
The tables show linear relationships between x and y. Write an equation in slope-intercept form for each relationship.
Question 10.
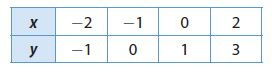
Type below:
____________
Answer:
Slope m = (y2 -y1)/(x2 – x1) = (3 – 1)/(2 – 0) = 2/2 = 1
y-intercept b = 1
Substituting the value of the slope m and y-intercept in the slope-intercept form. y = mx + b where, m = 1 and b = 1.
y = x + 1
Question 11.
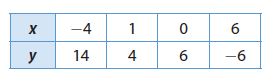
Type below:
____________
Answer:
Slope m = (y2 -y1)/(x2 – x1) = (6 – 4)/(0 – 1) = -2/1 = -2
y-intercept b = 6
Substituting the value of the slope m and y-intercept in the slope-intercept form. y = mx + b where, m = -2 and b = 6.
y = -2x + 6
Writing Linear Equations from a Table – Page No. 138
Question 12.
Finance
Desiree starts a savings account with $125.00. Every month, she deposits $53.50.
a. Complete the table to model the situation.

Type below:
____________
Answer:
![]()
Question 12.
b. Write an equation in slope-intercept form that shows how much money Desiree has in her savings account after x months.
Type below:
____________
Answer:
y = 53.5x + 125
Explanation:
Desiree starts a savings account with $125.00. Every month, she deposits $53.50.
Substituting the value of the slope m and y-intercept in the slope-intercept form. y = mx + b where, m = 53.5 and b = 125.
y = 53.5x + 125
Question 12.
c. Use the equation to find how much money Desiree will have in savings after 11 months.
$ ________
Answer:
$713.5
Explanation:
y = 53.5x + 125
The value of x is 11
y = 53.5 (11) + 125 = 588.5 + 125 = 713.5
Desiree will have $713.5 in savings after 11 months.
Question 13.
Monty documented the amount of rain his farm received on a monthly basis, as shown in the table.

a. Is the relationship linear? Why or why not?
Type below:
____________
Answer:
No
Explanation:
The change in the months is constant but the change in rainfall is not constant.
Question 13.
b. Can an equation be written to describe the amount of rain? Explain.
Type below:
____________
Answer:
No
Explanation:
There is no apparent pattern in the given data.
H.O.T.
Focus on Higher Order Thinking
Question 14.
Analyze Relationships
If you have a table that shows a linear relationship, when can you read the value for b, in y = mx + b, directly from the table without drawing a graph or doing any calculations? Explain.
Type below:
____________
Answer:
You can read the value of b directly from the table whrn the table contains the input value of 0 and its corresponding output values (value of y when x = 0)
Question 15.
What If?
Jaíme graphed linear data given in the form (cost, number). The y-intercept was 0. Jayla graphed the same data given in the form (number, cost). What was the y-intercept of her graph? Explain.
Type below:
____________
Answer:
Jaíme graphed linear data given in the form (cost, number). The y-intercept was 0. Jayla graphed the same data given in the form (number, cost).
Jaíme’s graph contained (0, 0). Since Jayal’s data were the same y-intercept is 0 but x and y are switched.
Guided Practice – Linear Relationships and Bivariate Data – Page No. 144
Use the following graphs to find the equation of the linear relationship.
Question 1.
Type below:
____________
Answer:
y = 30x
Explanation:
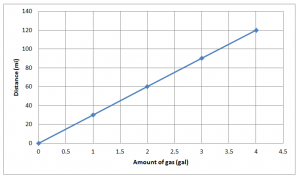
Find the slope using two points from the grapgh by
Slope m = (y2 -y1)/(x2 – x1) where (x1, y1) = (1, 30) and (x2, y2) = (2, 60)
Slope m = (y2 -y1)/(x2 – x1) = (60 – 30)/(2 – 1) = 30/1 = 30
y-intercept b = 0
Substituting the value of the slope m and y-intercept in the slope-intercept form. y = mx + b where, m = 30 and b = 0.
y = 30x
Question 2.
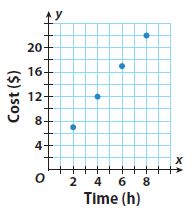
Type below:
____________
Answer:
y = 2.5x + 2
Explanation:
Find the slope using two points from the grapgh by
Slope m = (y2 -y1)/(x2 – x1) where (x1, y1) = (2, 7) and (x2, y2) = (4, 12)
Slope m = (y2 -y1)/(x2 – x1) = (12 – 7)/(4 – 2) = 5/2 = 2.5
y-intercept b = 2
Substituting the value of the slope m and y-intercept in the slope-intercept form. y = mx + b where, m = 2.5 and b = 2.
y = 2.5x + 2
Question 3.
The graph shows the relationship between the number of hours a kayak is rented and the total cost of the rental. Write an equation of the relationship. Then use the equation to predict the cost of a rental that lasts 5.5 hours.

Type below:
____________
Answer:
y = 20x + 30
The cost of a rental that lasts 5.5 hours is $140
Explanation:
Find the slope using two points from the grapgh by
Slope m = (y2 -y1)/(x2 – x1) where (x1, y1) = (2, 70) and (x2, y2) = (4, 110)
Slope m = (y2 -y1)/(x2 – x1) = (110 – 70)/(4 – 2) = 40/2 = 20
y-intercept b = 30
Substituting the value of the slope m and y-intercept in the slope-intercept form. y = mx + b where, m = 20 and b = 30.
y = 20x + 30
Substitue the value of x is 5.5 hrs
y = 20 (5.5) + 30
y = 110 + 30 = 140
The cost of a rental that lasts 5.5 hours is $140
Does each of the following graphs represent a linear relationship? Why or why not?
Question 4.
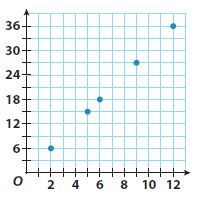
____________
Answer:
Yes; The graph has a constant rate of change
Explanation:
Find the slope using two points from the grapgh by
Slope m = (y2 -y1)/(x2 – x1) where (x1, y1) = (2, 6) and (x2, y2) = (5, 15)
Slope m = (y2 -y1)/(x2 – x1) = (15 – 6)/(5 – 2) = 9/3 = 3
y-intercept b = 6
Substituting the value of the slope m and y-intercept in the slope-intercept form. y = mx + b where, m = 3 and b = 6.
y = 3x + 6
The values changing according to the constant change in the x values.
Question 5.
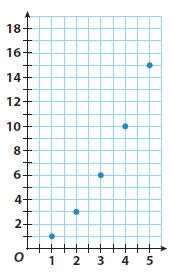
____________
Answer:
No; The graph does not have a constant rate of change
Essential Question Check-In
Question 6.
How can you tell if a set of bivariate data shows a linear relationship?
Type below:
____________
Answer:
It is a linear relationship if the rate of change is constant or the graph is a straight line.
Independent Practice – Linear Relationships and Bivariate Data – Page No. 145
Does each of the following tables represent a linear relationship? Why or why not?
Question 7.
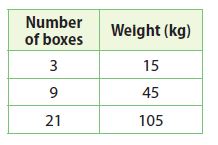
____________
Answer:
Linear Relationship
Explanation:
Find Rate of Change using Slope m = (y2 -y1)/(x2 – x1)
Rate of Change = (45 – 15)/(9 – 3) = 30/6 = 5
Rate of Change = (105 – 45)/(21 – 9) = 60/12 = 5
It is a Linear Relationship as the rate of the change is constant.
Question 8.
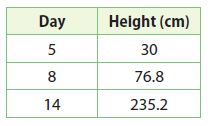
____________
Answer:
not a Linear Relationship
Explanation:
Find Rate of Change using Slope m = (y2 -y1)/(x2 – x1)
Rate of Change = (76.8 – 30)/(8 – 5) = 46./3 = 15.6
Rate of Change = (235.2 – 76.8)/(14 – 8) = 158.4/6 = 26.4
It is not a Linear Relationship as the rate of the change is varies.
Explain whether or not you think each relationship is linear.
Question 9.
the cost of equal-priced DVDs and the number purchased
____________
Answer:
y = cx
Explanation:
The relation between the cost of equal-priced DVDs and the number purchased is linear because the change rate is constant. If we denote with c the cost of a DVD, with x the number of purchased DVDs and with y the total cost of the purchased DVDs, we get an equation of the form:
y = cx
Question 10.
the height of a person and the person’s age
____________
Answer:
Non – Linear relationship
Explanation:
The height of a person does not increase at a constant rate with a person’s age
Question 11.
the area of a square quilt and its side length
____________
Answer:
Non – Linear relationship
Explanation:
The rate of change in the area of a square quilt increase as the side length increases.
Question 12.
the number of miles to the next service station and the number of kilometers
____________
Answer:
Linear relationship
Explanation:
The number of miles increases at a constant rate with the number of kilometers.
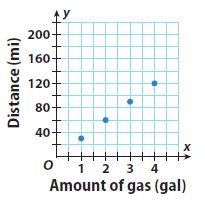
Question 13.
Multistep
The Mars Rover travels 0.75 feet in 6 seconds. Add the point to the graph. Then determine whether the relationship between distance and time is linear, and if so, predict the distance that the Mars Rover would travel in 1 minute.
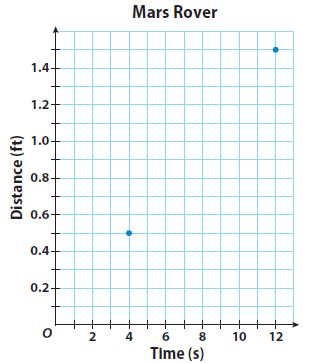
Distance traveled in 1 min.: _______ ft.
Answer:
Relationship is linear
Distance traveled in 1 min.: 7.5 ft.
Explanation:
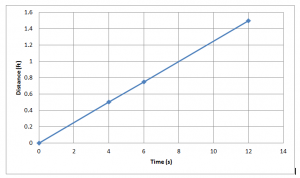
The graph is a straight line. So, the Relationship is linear
The equation representing the relationship between distance and time.
y = 0.125x
The value of x is 1 min = 60 sec
y = 0.125 (60) = 7.5 ft
Distance traveled in 1 min.: 7.5 ft.
Linear Relationships and Bivariate Data – Page No. 146
Question 14.
Make a Conjecture
Zefram analyzed a linear relationship, found that the slope-intercept equation was y=3.5x+16, and made a prediction for the value of y for a given value of x. He realized that he made an error calculating the y-intercept and that it was actually 12. Can he just subtract 4 from his prediction if he knows that the slope is correct? Explain.
____________
Answer:
Yes
Explanation:
The value of y is calculated using y = 3.5x+ 16. Since the slope of the point remains the same, 4 can be subtracted from the predicted answer as the value of y would be: y = 3.5x+ 16 – 4
H.O.T.
Focus on Higher Order Thinking
Question 15.
Communicate Mathematical Ideas
The table shows a linear relationship. How can you predict the value of y when x = 6 without finding the equation of the relationship?
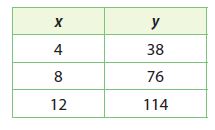
Type below:
____________
Answer:
57
Explanation:
Find Rate of Change using Slope m = (y2 -y1)/(x2 – x1)
Rate of Change = (76 – 38)/(8 – 4) = 38/4 = 9.5
Since the difference between 8 and S is 2, subtract twice the value of the rate of change from 76
y = 76 – (9.5 × 2) =57
Question 16.
Critique Reasoning
Louis says that if the differences between the values of x are constant between all the points on a graph, then the relationship is linear. Do you agree? Explain.
____________
Answer:
No
Explanation:
The difference between y should be constant for a constant interval of x.
Question 17.
Make a Conjecture
Suppose you know the slope of a linear relationship and one of the points that its graph passes through. How could you predict another point that falls on the graph of the line?
Type below:
____________
Answer:
Find the equation of the linear relationship using the slope and given point. The insert any x-value to find a y value on the graph of the line.
Question 18.
Explain the Error
Thomas used (7, 17.5) and (18, 45) from a graph to find the equation of a linear relationship as shown. What was his mistake?
m = \(\frac{45-7}{18-17.5}=\frac{38}{0.5}\) = 79
y = 79x + b =
49 = 79 × 18 + b
45 = 1422 + b, so b = −1337
The equation is y = 79x − 1377
Type below:
____________
Answer:
He subtracted the x value of the first point from the y of the second point and the y value of the second point from the x value of the first point.
Hence, the slope is incorrect and the equation is incorrect as well. The correct slope is
(45 – 17.5)/(18 – 7) = 27.5/11 = 2.5
5.1 Writing Linear Equations from Situations and Graphs – Model Quiz – Page No. 147
Write the equation of each line in slope-intercept form.
Question 1.
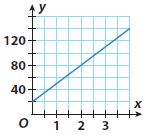
Type below:
____________
Answer:
y = 30x + 20
Explanation:
Find the slope using two points from the graph by m = (y2 -y1)/(x2 – x1) where (x1, y1) = (0, 20), (x2, y2) = (2, 80)
Substitute the value of m and (x1, y1) = (0, 20), (x2, y2) = (2, 80)
Slope m = (y2 -y1)/(x2 – x1) = (80 – 20)/(2 – 0) = 60/2 = 30
Substituting the value of slope (m) and (x, y) in the slope intercept form to find y intercept (b):
80 = 30(2) + b
y-intercept b = 20
Substituting the value of the slope m and y-intercept in the slope-intercept form. y = mx + b where, m = 30 and b = 20.
y = 30x + 20
Question 2.
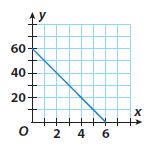
Type below:
____________
Answer:
y = -10x + 60
Explanation:
Find the slope using two points from the graph by m = (y2 -y1)/(x2 – x1) where (x1, y1) = (6, 0), (x2, y2) = (0, 60)
Substitute the value of m and (x1, y1) = (6, 0), (x2, y2) = (0, 60)
Slope m = (y2 -y1)/(x2 – x1) = (60 – 0)/(0 – 6) = -60/6 = -10
Substituting the value of slope (m) and (x, y) in the slope intercept form to find y intercept (b):
60 = -10(0) + b
y-intercept b = 60
Substituting the value of the slope m and y-intercept in the slope-intercept form. y = mx + b where, m = -10 and b = 60.
y = -10x + 60
5.2 Writing Linear Equations from a Table
Write the equation of each linear relationship in slope-intercept form.
Question 3.
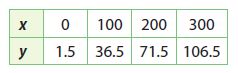
Type below:
____________
Answer:
y = 0.35x + 1.5
Explanation:
Find the slope using two points from the graph by m = (y2 -y1)/(x2 – x1) where (x1, y1) = (0, 1.5), (x2, y2) = (100, 36.5)
Substitute the value of m and (x1, y1) = (0, 1.5), (x2, y2) = (100, 36.5)
Slope m = (y2 -y1)/(x2 – x1) = (36.5 – 1.5)/(100 – 0) = 35/100 = 0.35
Substituting the value of slope (m) and (x, y) in the slope intercept form to find y intercept (b):
1.5 =0.35(0) + b
y-intercept b = 1.5
Substituting the value of the slope m and y-intercept in the slope-intercept form. y = mx + b where, m = 0.35 and b = 1.5.
y = 0.35x + 1.5
Question 4.
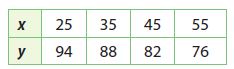
Type below:
____________
Answer:
y = -0.6x + 109
Explanation:
Find the slope using two points from the graph by m = (y2 -y1)/(x2 – x1) where (x1, y1) = (25, 94), (x2, y2) = (35, 88)
Substitute the value of m and (x1, y1) = (25, 94), (x2, y2) = (35, 88)
Slope m = (y2 -y1)/(x2 – x1) = (88 – 94)/(35 – 25) = -6/10 = -0.6
Substituting the value of slope (m) and (x, y) in the slope intercept form to find y intercept (b):
88 = -0.6(35) + b
y-intercept b = 109
Substituting the value of the slope m and y-intercept in the slope-intercept form. y = mx + b where, m = -0.6 and b = 109.
y = -0.6x + 109
5.3 Linear Relationships and Bivariate Data
Write the equation of the line that connects each set of data points.
Question 5.
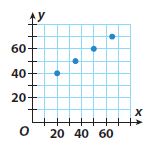
Type below:
____________
Answer:
y = 2/3x + 26 2/3
Explanation:
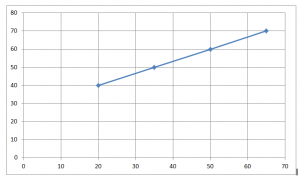
Find the slope using two points from the graph by m = (y2 -y1)/(x2 – x1) where (x1, y1) = (20, 40), (x2, y2) = (50, 60)
Substitute the value of m and (x1, y1) = (20, 40), (x2, y2) = (50, 60)
Slope m = (y2 -y1)/(x2 – x1) = (60 – 40)/(50 – 20) = 20/30 = 2/3
Substituting the value of slope (m) and (x, y) in the slope intercept form to find y intercept (b):
40 = 2/3(20) + b
y-intercept b = 26 2/3
Substituting the value of the slope m and y-intercept in the slope-intercept form. y = mx + b where, m = 2/3 and b = 26 2/3.
y = 2/3x + 26 2/3
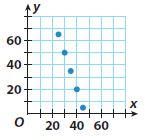
Question 6.
Type below:
____________
Answer:
y = -3x + 140
Explanation:
Find the slope using two points from the graph by m = (y2 -y1)/(x2 – x1) where (x1, y1) = (25, 65), (x2, y2) = (30, 50)
Substitute the value of m and (x1, y1) = (25, 65), (x2, y2) = (30, 50)
Slope m = (y2 -y1)/(x2 – x1) = (50 – 65)/(30 – 25) = -15/5 = -3
Substituting the value of slope (m) and (x, y) in the slope intercept form to find y intercept (b):
50 = -3(30) + b
y-intercept b = 140
Substituting the value of the slope m and y-intercept in the slope-intercept form. y = mx + b where, m = -3 and b = 140.
y = -3x + 140
Essential Question
Question 7.
Write a real-world situation that can be represented by a linear relationship.
Type below:
____________
Answer:
There is an hourly fee of $15 for renting the ski gears per hour and an entry fee of $10 for the ski lodge.
Selected Response – Mixed Review – Page No. 148
Question 1.
An hourglass is turned over with the top part filled with sand. After 3 minutes, there are 855 mL of sand in the top half. After 10 minutes, there are 750 mL of sand in the top half. Which equation represents this situation?
Options:
a. y = 285x
b. y = −10.5x + 900
c. y = −15x + 900
d. y = 75x
Answer:
c. y = −15x + 900
Explanation:
Identify the input and output variable
Input: Number of minutes
Output: Quantity of sand in the hourglass
Write the given information as ordered pair (3, 855), (10, 750)
Find the slope using two points from the graph by m = (y2 -y1)/(x2 – x1) where (x1, y1) = (10, 750), (x2, y2) =(3, 855)
Substitute the value of m and (x1, y1) = (10, 750), (x2, y2) =(3, 855)
Slope m = (y2 -y1)/(x2 – x1) = (855 – 750)/(3 – 10) = -105/7 = -15
Substituting the value of slope (m) and (x, y) in the slope intercept form to find y intercept (b):
750 = -15(10) + b
y-intercept b = 900
Substituting the value of the slope m and y-intercept in the slope-intercept form. y = mx + b where, m = -15 and b = 900.
y = -15x + 900
Question 2.
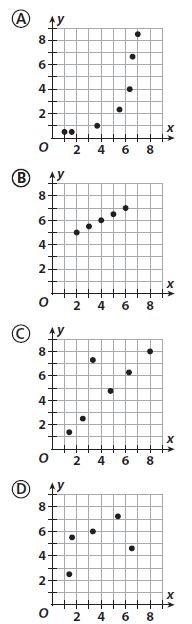
Which graph shows a linear relationship?
Options:
a. A
b. B
c. C
d. D
Answer:
b. B
Explanation:
Graph B represents the linear relationship
The data appears to lie on a straight line
Question 3.
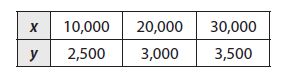
What are the slope and y-intercept of the relationship shown in the table?
Options:
a. slope = 0.05, y-intercept = 1,500
b. slope = 0.5, y-intercept = 1,500
c. slope = 0.05, y-intercept = 2,000
d. slope = 0.5, y-intercept = 2,000
Answer:
c. slope = 0.05, y-intercept = 2,000
Explanation:
Find the slope using two points from the graph by m = (y2 -y1)/(x2 – x1) where (x1, y1) = (10,000, 2,500), (x2, y2) =(20,000, 3,000)
Substitute the value of m and (x1, y1) = (10,000, 2,500), (x2, y2) =(20,000, 3,000)
Slope m = (y2 -y1)/(x2 – x1) = (3,000 – 2,500)/(20,000 – 10,000) = 500/10,000 = 0.05
Substituting the value of slope (m) and (x, y) in the slope intercept form to find y intercept (b):
3,000 = 0.05(20,000) + b
y-intercept b = 2,000
Question 4.
Which is the sum of 3.15 × 107 + 9.3 × 106? Write your answer in scientific notation.
Options:
a. 4.08 × 107
b. 4.08 × 106
c. 0.408 × 108
d. 40.8 × 106
Answer:
a. 4.08 × 107
Explanation:
Given 3.15 × 107 + 9.3 × 106?
(3.15 + 0.93) × 107
4.08 × 107
Mini-Task
Question 5.
Franklin’s faucet was leaking, so he put a bucket underneath to catch the water. After a while, Franklin started keeping track of how much water was in the bucket. His data is in the table below.
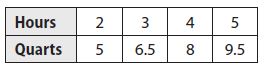
a. Is the relationship linear or nonlinear?
_____________
Answer:
The relationship linear
Explanation:
Find the rate of change by Difference in Quarts/Hours
(6.5 – 5)/(3 – 2) = 1.5
(8 – 6.5)/(4 – 3) = 1.5
(9.5 – 8)/(5 – 4) = 1.5
Since the rate of change is constant, the relationship is linear.
Question 5.
b. Write the equation for the relationship.
Type below:
_____________
Answer:
Rate of change is the slope of the linear equation
m = 1.5
Question 5.
c. Predict how much water will be in the bucket after 14 hours if Franklin doesn’t stop the leak.
_______ quarts
Answer:
23 quarts
Explanation:
Substituting the value of slope (m) and (x, y) in the slope intercept form to find y-intercept (b)
y = mx + b
5 = 1.5(2) + b
y-intercept b = 2
Substituting the value of the slope m and y-intercept in the slope-intercept form. y = mx + b where, m = 1.5 and b = 2.
y = 1.5x + 2
The x value is 2
y = 1.5(2) + 2 = 23
There will be 23 quarts after 14 hrs.
Conclusion:
Every expert’s choice is utilizing Go math Grade 8 Chapter 5 Writing Linear Equations Answer Key PDF. Practice the question from our Go Math 8th Grade Chapter 5 Writing Linear Equations Answers to score the highest marks in the exams. Compare the questions with the real-time problems and solve the problems with the help of Go Math Grade 8 Chapter 5 Answer Key Chapter 5 Writing Linear Equations. Stay tuned to our eurekamathanswerkeys.com to get the all Go Math Grade 8 Answer Key Chapterwise pdfs.