Eureka Math Grade 8 Module 1 Lesson 1 Answer Key

Engage NY Eureka Math 8th Grade Module 1 Lesson 1 Answer Key

Eureka Math Grade 8 Module 1 Lesson 1 Example Answer Key

Example 1-5
Work through Examples 1–5 as a group, and supplement with additional examples if needed.

Example 1.
5×5×5×5×5×5=
Answer:
5⁶

Example 2.
$\frac{9}{7}$×$\frac{9}{7}$×$\frac{9}{7}$×$\frac{9}{7}$=
Answer:
($\frac{9}{7}$)⁴

Example 3.
(-$\frac{4}{11}$)³=
Answer:
(-$\frac{4}{11}$)×(-$\frac{4}{11}$)×(-$\frac{4}{11}$)

Example 4.
(-2)⁶=
Answer:
(-2)×(-2)×(-2)×(-2)×(-2)×(-2)

Example 5.
3.8⁴=3.8×3.8×3.8×3.8

Eureka Math Grade 8 Module 1 Lesson 1 Exercise Answer Key

Exercise 1.
$Eureka Math Grade 8 Module 1 Lesson 1 Exercise Answer Key 1$
Answer:
4⁷

Exercise 2.
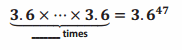
$Eureka Math Grade 8 Module 1 Lesson 1 Exercise Answer Key 2$
Answer:

Exercise 3.
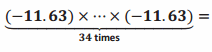
$Eureka Math Grade 8 Module 1 Lesson 1 Exercise Answer Key 3$
Answer:
(-11.63)³⁴

Exercise 4.
$Eureka Math Grade 8 Module 1 Lesson 1 Exercise Answer Key 4$
Answer:
15 times

Exercise 5.
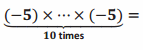
$Eureka Math Grade 8 Module 1 Lesson 1 Exercise Answer Key 5$
=(-5)¹⁰

Exercise 6.
$Eureka Math Grade 8 Module 1 Lesson 1 Exercise Answer Key 6$
Answer:
($\frac{7}{2}$)²¹

Exercise 7.
$Eureka Math Grade 8 Module 1 Lesson 1 Exercise Answer Key 7$
Answer:
(-13)⁶

Exercise 8.
$Eureka Math Grade 8 Module 1 Lesson 1 Exercise Answer Key 8$
Answer:
(-$\frac{1}{14}$)¹⁰

Exercise 9.
$Eureka Math Grade 8 Module 1 Lesson 1 Exercise Answer Key 9$
Answer:
x¹⁸⁵

Exercise 10.
$Eureka Math Grade 8 Module 1 Lesson 1 Exercise Answer Key 10$
Answer:
n times

Exercise 11.
Will these products be positive or negative? How do you know?
$Eureka Math Grade 8 Module 1 Lesson 1 Exercise Answer Key 11$
Answer:
This product will be positive. Students may state that they computed the product and it was positive. If they say that, let them show their work. Students may say that the answer is positive because the exponent is positive; however, this would not be acceptable in view of the next example.

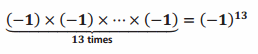
$Eureka Math Grade 8 Module 1 Lesson 1 Exercise Answer Key 12$
This product will be negative. Students may state that they computed the product and it was negative. If so, ask them to show their work. Based on the discussion of the last problem, you may need to point out that a positive exponent does not always result in a positive product.

The two problems in Exercise 12 force the students to think beyond the computation level. If students struggle, revisit the previous two problems, and have them discuss in small groups what an even number of negative factors yields and what an odd number of negative factors yields.

Exercise 12.
Is it necessary to do all of the calculations to determine the sign of the product? Why or why not?
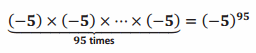
$Eureka Math Grade 8 Module 1 Lesson 1 Exercise Answer Key 13$
Answer:
Students should state that an odd number of negative factors yields a negative product.
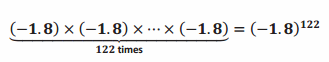
$Eureka Math Grade 8 Module 1 Lesson 1 Exercise Answer Key 14$
Students should state that an even number of negative factors yields a positive product.

Exercise 13.
Fill in the blanks indicating whether the number is positive or negative.
If n is a positive even number, then (-55)ⁿ is _____
Answer:
positive.
If n is a positive odd number, then (-72.4)ⁿ is __
Answer:
negative.

Exercise 14.
Josie says that $Eureka Math Grade 8 Module 1 Lesson 1 Exercise Answer Key 15$ Is she correct? How do you know?
Answer:
Students should state that Josie is not correct for the following two reasons: (1) They just stated that an even number of factors yields a positive product, and this conflicts with the answer Josie provided, and (2) the notation is used incorrectly because, as is, the answer is the negative of 15⁶, instead of the product of 6 copies of -15. The base is (-15). Recalling the discussion at the beginning of the lesson, when the base is negative it should be written clearly by using parentheses. Have students write the answer correctly.

Eureka Math Grade 8 Module 1 Lesson 1 Problem Set Answer Key

Question 1.
Use what you know about exponential notation to complete the expressions below.
$Eureka Math Grade 8 Module 1 Lesson 1 Problem Set Answer Key 15.1$
Answer:
(-5)¹⁷

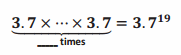
$Eureka Math Grade 8 Module 1 Lesson 1 Problem Set Answer Key 16$
Answer:
19 times

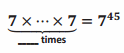
$Eureka Math Grade 8 Module 1 Lesson 1 Problem Set Answer Key 17$
Answer:
45 times

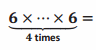
$Eureka Math Grade 8 Module 1 Lesson 1 Problem Set Answer Key 18$
Answer:
6⁴

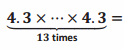
$Eureka Math Grade 8 Module 1 Lesson 1 Problem Set Answer Key 19$
=4.3¹³

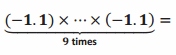
$Eureka Math Grade 8 Module 1 Lesson 1 Problem Set Answer Key 20$
Answer:
(-1.1)⁹

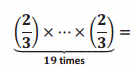
$Eureka Math Grade 8 Module 1 Lesson 1 Problem Set Answer Key 21$
($\frac{2}{3}$)¹⁹

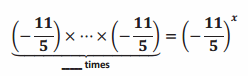
$Eureka Math Grade 8 Module 1 Lesson 1 Problem Set Answer Key 22$
(-$\frac{11}{5}$)^x
Answer:
x times

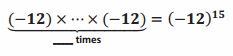
$Eureka Math Grade 8 Module 1 Lesson 1 Problem Set Answer Key 23$
Answer:
15 times

$Eureka Math Grade 8 Module 1 Lesson 1 Problem Set Answer Key 24$
Answer:
a^m

Question 2.
Write an expression with (-1) as its base that will produce a positive product, and explain why your answer is valid.
Answer:
Accept any answer with (-1) to an exponent that is even.

Question 3.
Write an expression with (-1) as its base that will produce a negative product, and explain why your answer is valid.
Answer:
Accept any answer with (-1) to an exponent that is odd.

Question 4.
Rewrite each number in exponential notation using 2 as the base.
Answer:
8=
Answer:
2³

16=
Answer:
2⁴

32 =
Answer:
2⁵

64=
Answer:
2⁶

128=
Answer:
2⁷

256=
Answer:
2⁸

Question 5.
Tim wrote 16 as (-2)⁴. Is he correct? Explain.
Answer:
Tim is correct that 16=(-2)⁴. (-2)(-2)(-2)(-2)=(4)(4)=16.

Question 6.
Could -2 be used as a base to rewrite 32? 64? Why or why not?
Answer:
A base of -2 cannot be used to rewrite 32 because (-2)⁵=-32. A base of -2 can be used to rewrite 64 because (-2)⁶=64. If the exponent, n, is even, (-2)ⁿ will be positive. If the exponent, n, is odd, (-2)ⁿ cannot be a positive number.

Eureka Math Grade 8 Module 1 Lesson 1 Exit Ticket Answer Key

Question 1.
a. Express the following in exponential notation:
$Engage NY Math 8th Grade Module 1 Lesson 1 Exit Ticket Answer Key 15.3$
Answer:
(-13)³⁵

b. Will the product be positive or negative? Explain.
Answer:
The product will be negative. The expanded form shows 34 negative factors plus one more negative factor. Any even number of negative factors yields a positive product. The remaining 35th negative factor negates the resulting product.

Question 2.
Fill in the blank:
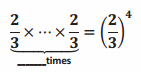
$Engage NY Math 8th Grade Module 1 Lesson 1 Exit Ticket Answer Key 36$
Answer:
4 times

Question 3.
Arnie wrote:
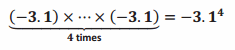
$Engage NY Math 8th Grade Module 1 Lesson 1 Exit Ticket Answer Key 37$
Is Arnie correct in his notation? Why or why not?
Answer:
Arnie is not correct. The base, -3.1, should be in parentheses to prevent ambiguity. At present the notation is not correct.