Engage NY Eureka Math 7th Grade Module 6 Lesson 13 Answer Key
Eureka Math Grade 7 Module 6 Lesson 13 Example Answer Key
Example 1.

Answer:
The triangles are identical by the two angles and the included side condition. The correspondence △ABC↔△YXZ matches two pairs of angles and one pair of equal sides. Since both triangles have parts under the condition of the same measurement, the triangles must be identical.
In Example 2 and Exercises 4–6, three pieces of information are given for △ABC and △XYZ. Draw, freehand, the two triangles (do not worry about scale), and mark the given information. If the triangles are identical, give a triangle correspondence that matches equal angles and equal sides. Explain your reasoning.
Example 2.
AB = XZ, AC = XY, ∠A = ∠X
Answer:
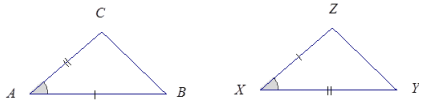
These triangles are identical by the two sides and included angle condition. The triangle correspondence △ABC ↔ △XZY matches two pairs of equal sides and one pair of equal, included angles. Since both triangles have parts under the condition of the same measurement, the triangles must be identical.
Eureka Math Grade 7 Module 6 Lesson 13 Exercise Answer Key
Opening Exercise
a. List all the conditions that determine unique triangles.
b. How are the terms identical and unique related?
Answer:
a.
→ Three sides condition
→ Two sides and included angle condition
→ Two angles and included side condition
→ Two angles and the side opposite a given angle condition
→ Two sides and a non-included angle, provided the angle is 90° or greater
→ Two sides and a non-included angle, provided the side adjacent to the angle is shorter than the side opposite the angle.
b. When drawing a triangle under a given condition, the triangle will either be identical or non-identical to the original triangle. If only one triangle can be drawn under the condition, we say the condition determines a unique triangle. A triangle drawn under a condition that is known to determine a unique triangle will be identical to the original triangle.
Each of the following problems gives two triangles. State whether the triangles are identical, not identical, or not necessarily identical. If the triangles are identical, give the triangle conditions that explain why, and write a triangle correspondence that matches the sides and angles. If the triangles are not identical, explain why. If it is not possible to definitively determine whether the triangles are identical, write “the triangles are not necessarily identical,” and explain your reasoning.
Exercises 1–3
1.
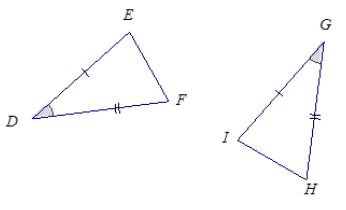
Answer:
The triangles are identical by the two sides and the included angle condition. The correspondence △DEF↔△GIH matches two equal pairs of sides and one equal pair of angles. Since both triangles have parts under the condition of the same measurement, the triangles must be identical.
2.
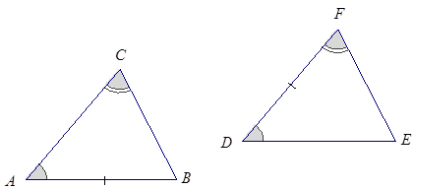
Answer:
The triangles are not necessarily identical. Although the two angles in each triangle match, the marked sides do not correspond. In △ABC, the marked side is not between the marked angles; whereas in △DEF, the marked side is between the marked angles.
3.
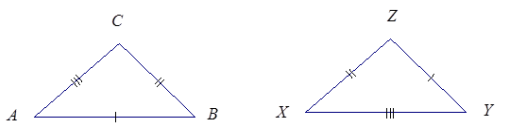
Answer:
The triangles are identical by the three sides condition. The correspondence △ABC↔△YZX matches three equal pairs of sides. Since both triangles have the same side lengths, the triangles must be identical.
Exercises 4–6
4. ∠A = ∠Z, ∠B = ∠Y, AB = YZ
Answer:

These triangles are identical by the two angles and included side condition. The triangle correspondence
△ABC ↔ △ZYX matches two pairs of equal angles and one pair of equal, included sides. Since both triangles have parts under the condition of the same measurement, the triangles must be identical.
5. ∠A = ∠Z, ∠B = ∠Y, BC = XY
Answer:
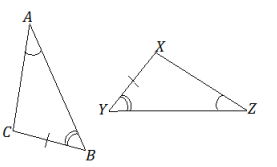
These triangles are identical by the two angles and side opposite a given angle condition. The triangle correspondence △ABC ↔ △ZYX matches two pairs of equal angles and one pair of equal sides. Since both triangles have parts under the condition of the same measurement, the triangles must be identical.
6. ∠A = ∠Z, ∠B = ∠Y, BC = XZ
Answer:
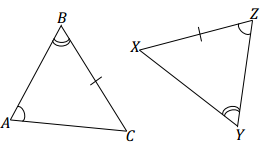
These triangles are not necessarily identical. In △ABC, the marked side is opposite ∠A. In △XYZ, the marked side is not opposite ∠Z, which is equal to ∠A. Rather, it is opposite ∠Y, which is equal to ∠B.
Eureka Math Grade 7 Module 6 Lesson 13 Problem Set Answer Key
In each of the following four problems, two triangles are given. State whether the triangles are identical, not identical, or not necessarily identical. If the triangles are identical, give the triangle conditions that explain why, and write a triangle correspondence that matches the sides and angles. If the triangles are not identical, explain why. If it is not possible to definitively determine whether the triangles are identical, write “the triangles are not necessarily identical,” and explain your reasoning.
Question 1.

Answer:
The triangles are identical by the two angles and included side condition. The correspondence △MNO↔△RQP matches two equal pairs of angles and one equal pair of included sides. Since both triangles have parts under the condition of the same measurement, the triangles must be identical.
Question 2.
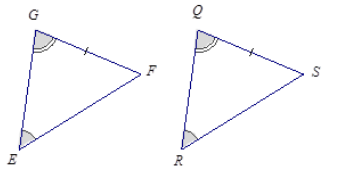
Answer:
The triangles are identical by the two angles and side opposite a given angle condition. The correspondence △EGF ↔ △RQS matches two equal pairs of angles and one equal pair of sides. Since both triangles have parts under the condition of the same measurement, the triangles must be identical.
Question 3.
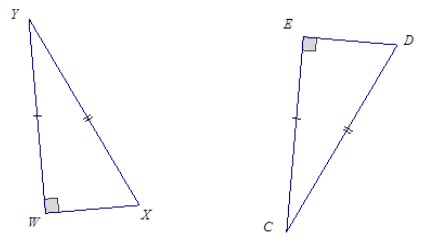
Answer:
The triangles are identical by the two sides and non-included 90° (or greater) angle condition. The correspondence △WXY ↔ △EDC matches two pairs of equal sides and one pair of equal angles. Since both triangles have parts under the condition of the same measurement, the triangles must be identical.
Question 4.
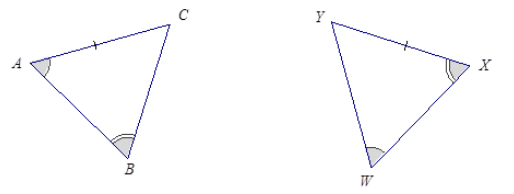
Answer:
The triangles are not necessarily identical by the two angles and side opposite a given angle condition. In △ABC, the marked side is adjacent to the angle marked with a single arc mark. In △WXY, the marked side is not adjacent to the angle marked with a single arc mark.
For Problems 5–8, three pieces of information are given for △ABC and △YZX. Draw, freehand, the two triangles (do not worry about scale), and mark the given information. If the triangles are identical, give a triangle correspondence that matches equal angles and equal sides. Explain your reasoning.
Question 5.
AB = YZ, BC = ZX, AC = YX
Answer:

These triangles are identical by the three sides condition. The triangle correspondence △ABC ↔ △YZX matches three pairs of equal sides. Since both triangles have parts under the condition of the same measurement, the triangles must be identical.
Question 6.
AB = YZ, BC = ZX, ∠C = ∠Y
Answer:
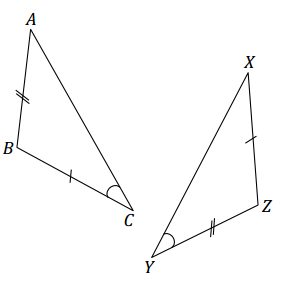
These triangles are not necessarily identical. In △ABC, the marked angle is adjacent to \(\overline{B C}\). In △YZX, the marked angle is not adjacent to the side equal to ZX, which is equal to BC.
Question 7.
AB = XZ, ∠A = ∠Z, ∠C = ∠Y
Answer:
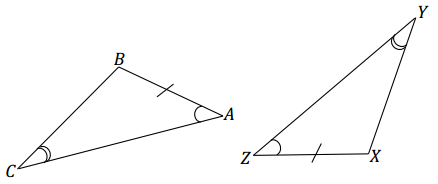
These triangles are identical by the two angles and a side opposite a given angle condition. The triangle correspondence △ABC ↔ △ZXY matches two pairs of equal angles and one pair of equal sides. Since both triangles have parts under the condition of the same measurement, the triangles must be identical.
Question 8.
AB = XY, AC = YZ, ∠C = ∠Z (Note that both angles are obtuse.)
Answer:
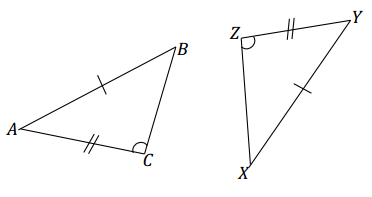
The triangles are identical by the two sides and non-included 90° (or greater) angle condition. The correspondence △ABC ↔ △YXZ matches two pairs of equal sides and one pair of equal angles. Since both triangles have parts under the condition of the same measurement, the triangles must be identical.
Eureka Math Grade 7 Module 6 Lesson 13 Exit Ticket Answer Key
Question 1.
∠A and ∠D are equal in measure. Draw two triangles around each angle, and mark parts appropriately so that the triangles are identical; use ∠A and ∠D as part of the chosen condition. Write a correspondence for the triangles.

Answer:
Answers will vary; students should select any condition except for the three sides condition and show the appropriate correspondence for their condition on the two triangles.