Engage NY Eureka Math 7th Grade Module 4 Lesson 16 Answer Key
Eureka Math Grade 7 Module 4 Lesson 16 Example Answer Key
Example 1.
A school has 60% girls and 40% boys. If 20% of the girls wear glasses and 40% of the boys wear glasses, what percent of all students wears glasses?
Answer:
Let n represent the number of students in the school.
The number of girls is 0.6n. The number of boys is 0.4n.

The number of girls wearing glasses is as follows: 0.2(0.6n) = 0.12n.
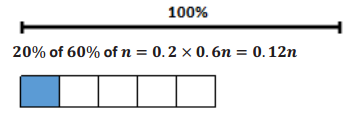
The number of boys wearing glasses is as follows: 0.4(0.4n) = 0.16n.
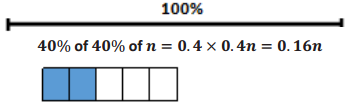
The total number of students wearing glasses is 0.12n + 0.16n = 0.28n.
0.28 = 28%, so 28% of the students wear glasses.
Example 2.
The weight of the first of three containers is 12% more than the second, and the third container is 20% lighter than the second. By what percent is the first container heavier than the third container?
Answer:
Let n represent the weight of the second container. (The tape diagram representation for the second container is divided into five equal parts to show 20%. This will be useful when drawing a representation for the third container and also when sketching a 12% portion for the first container since it will be slightly bigger than half of the 20% portion created.)
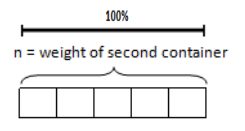
The weight of the first container is (1.12)n.

The weight of the third container is (0.80)n.
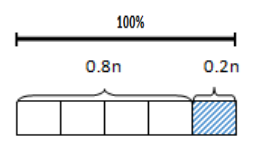
The following represents the difference in weight between the first and third container:
1.12n – 0.80n = 0.32n
Recall that the weight of the third container is 0.8n
0.32n ÷ 0.8n = 0.4. The first container is 40% heavier than the third container.
Or 1.4 × 100% = 140%, which also shows that the first container is 40% heavier than the third container.
Example 3.
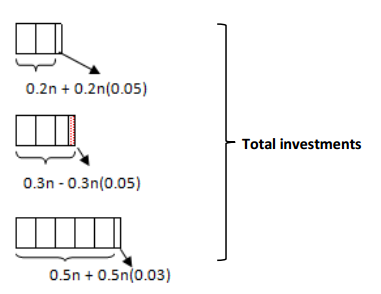
In one year’s time, 20% of Ms. McElroy’s investments increased by 5%, 30% of her investments decreased by 5%, and 50% of her investments increased by 3%. By what percent did the total of her investments increase?
Answer:
Let n represent the dollar amount of Ms. McElroy’s investments before the changes occurred during the year.
After the changes, the following represents the dollar amount of her investments:
0.2n(1.05) + 0.3n(0.95) + 0.5n(1.03)
= 0.21n + 0.285n + 0.515n
= 1.01n.
Since 1.01 = 101%, Ms. McElroy’s total investments increased by 1%.
Eureka Math Grade 7 Module 4 Lesson 16 Exercise Answer Key
Exercise 1.
How does the percent of students who wear glasses change if the percent of girls and boys remains the same (that is, 60% girls and 40% boys), but 20% of the boys wear glasses and 40% of the girls wear glasses?
Answer:
Let n represent the number of students in the school.
The number of girls is 0.6n. The number of boys is 0.4n.

Girls who wear glasses:
40% of 60% of n = 0.4 × 0.6n = 0.24n
Boys who wear glasses:

Students who wear glasses:
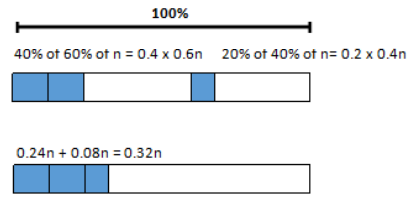
32% of students wear glasses.
Exercise 2.
How would the percent of students who wear glasses change if the percent of girls is 40% of the school and the percent of boys is 60% of the school, and 40% of the girls wear glasses and 20% of the boys wear glasses? Why?
Answer:
The number of students wearing glasses would be equal to the answer for Example 1 because all of the percents remain the same except that a swap is made between the boys and girls. So, the number of boys wearing glasses is swapped with the number of girls, and the number of girls wearing glasses is swapped with the number of boys, but the total number of students wearing glasses is the same.
Let n represent the number of students in the school.
The number of boys is 0.6n. The number of girls is 0.4n.

Boys who wear glasses:
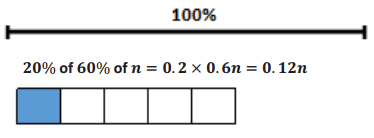
Girls who wear glasses:
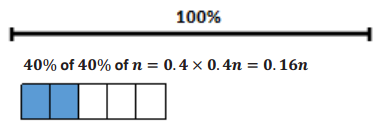
Students who wear glasses:

Exercise 3.
Matthew’s pet dog is 7% heavier than Harrison’s pet dog, and Janice’s pet dog is 20% lighter than Harrison’s. By what percent is Matthew’s dog heavier than Janice’s?
Answer:
Let h represent the weight of Harrison’s dog.
Matthew’s dog is 1.07h, and Janice’s dog is 0.8h.
Since 1.07 ÷ 0.8 = \(\frac{107}{80}\) = 1.3375, Mathew’s dog is 33.75% heavier than Janice’s dog.
Exercise 4.
A concert had 6,000 audience members in attendance on the first night and the same on the second night. On the first night, the concert exceeded expected attendance by 20%, while the second night was below the expected attendance by 20%. What was the difference in percent of concert attendees and expected attendees for both nights combined?
Answer:
Let x represent the expected number of attendees on the first night and y represent the number expected on the second night.
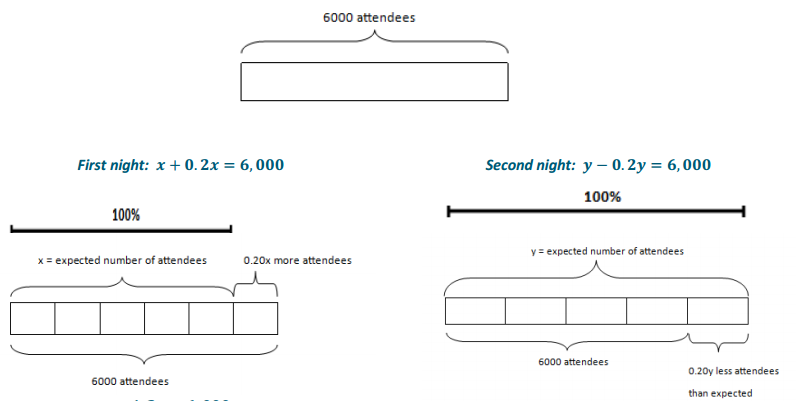
1.2x = 6,000
x = 5,000
6,000 – 5,000 = 1,000
The first night was attended by 1,000 more people than expected.
0.8y = 6,000
y = 7,500
7,500 – 6,000 = 1,500
The second night was attended by 1,500 less people than expected.
5,000 + 7,500 = 12,500
12,500 people were expected in total on both nights.
1,500 – 1,000 = 500. \(\frac{500}{12,500}\) × 100% = 4%. The concert missed its expected attendance by 4%.
Eureka Math Grade 7 Module 4 Lesson 16 Problem Set Answer Key
Question 1.
One container is filled with a mixture that is 30% acid. A second container is filled with a mixture that is 50% acid. The second container is 50% larger than the first, and the two containers are emptied into a third container. What percent of acid is the third container?
Answer:
Let t be the amount of mixture in the first container. Then the second container has 1.5t, and the third container has 2.5t.
The amount of acid in the first container is 0.3t, the amount of acid in the second container is 0.5(1.5t) = 0.75t, and the amount of acid in the third container is 1.05t. The percent of acid in the third container is
\(\frac{1.05}{2.5}\) × 100% = 42%.
Question 2.
The store’s markup on a wholesale item is 40%. The store is currently having a sale, and the item sells for 25% off the retail price. What is the percent of profit made by the store?
Answer:
Let w represent the wholesale price of an item.
Retail price: 1.4w
Sale price: 1.4w – (1.4w × 0.25) = 1.05w
The store still makes a 5% profit on a retail item that is on sale.
Question 3.
During lunch hour at a local restaurant, 90% of the customers order a meat entrée and 10% order a vegetarian entrée. Of the customers who order a meat entrée, 80% order a drink. Of the customers who order a vegetarian entrée, 40% order a drink. What is the percent of customers who order a drink with their entrée?
Answer:
Let e represent lunch entrées.
Meat entrées: 0.9e
Vegetarian entrées: 0.1e
Meat entrées with drinks: 0.9e × 0.8 = 0.72e
Vegetarian entrées with drinks: 0.1e × 0.4 = 0.04e
Entrées with drinks: 0.72e + 0.04e = 0.76e. Therefore, 76% of lunch entrées are ordered with a drink.
Question 4.
Last year’s spell – a – thon spelling test for a first grade class had 15% more words with four or more letters than this year’s spelling test. Next year, there will be 5% less than this year. What percent more words have four or more letters in last year’s test than next year’s?
Answer:
Let t represent this year’s amount of spell – a – thon words with four letters or more.
Last year: 1.15t
Next year: 0.95t
1.15 t ÷ 0.95t × 100% ≈ 121%. There were about 21% more words with four or more letters last year than there will be next year.
Question 5.
An ice cream shop sells 75% less ice cream in December than in June. Twenty percent more ice cream is sold in July than in June. By what percent did ice cream sales increase from December to July?
Answer:
Let j represent sales in June.
December: 0.25j
July: 1.20j
1.20 ÷ 0.25 = 4.8 × 100% = 480%. Ice cream sales in July increase by 380% from ice cream sales in December.
Question 6.
The livestock on a small farm the prior year consisted of 40% goats, 10% cows, and 50% chickens. This year, there is a 5% decrease in goats, 9% increase in cows, and 15% increase in chickens. What is the percent increase or decrease of livestock this year?
Answer:
Let l represent the number of livestock the prior year.
Goats decrease: 0.4l – (0.4l × 0.05) = 0.38l or 0.95(0.4l) = 0.38l
Cows increase: 0.1 l + (0.1l × 0.09 ) = 0.109l or 1.09(0.1l) = 0.109l
Chickens increase: 0.5k + ( 0.5k × 0.15) = 0.575l or 1.15(0.5l) = 0.575l
0.38l + 0.109l + 0.575l = 1.064l. There is an increase of 6.4% in livestock.
Question 7.
In a pet shelter that is occupied by 55% dogs and 45% cats, 60% of the animals are brought in by concerned people who found these animals in the streets. If 90% of the dogs are brought in by concerned people, what is the percent of cats that are brought in by concerned people?
Answer:
Let c represent the percent of cats brought in by concerned people.
0.55(0.9) + (0.45)(c) = 1(0.6)
0.495 + 0.45c = 0.6
0.495 – 0.495 + 0.45c = 0.6 – 0.495
0.45c = 0.105
0.45c ÷ 0.45 = 0.105 ÷ 0.45
c ≈ 0.233
About 23% of the cats brought into the shelter are brought in by concerned people.
Question 8.
An artist wants to make a particular teal color paint by mixing a 75% blue hue and 25% yellow hue. He mixes a blue hue that has 85% pure blue pigment and a yellow hue that has 60% of pure yellow pigment. What is the percent of pure pigment that is in the resulting teal color paint?
Answer:
Let p represent the teal color paint.
(0.75 × 0.85p) + (0.25 × 0.6p) = 0.7875p
78.75% of pure pigment is in the resulting teal color paint.
Question 9.
On Mina’s block, 65% of her neighbors do not have any pets, and 35% of her neighbors own at least one pet. If 25% of the neighbors have children but no pets, and 60% of the neighbors who have pets also have children, what percent of the neighbors have children?
Answer:
Let n represent the number of Mina’s neighbors.
Neighbors who do not have pets: 0.65n
Neighbors who own at least one pet: 0.35n
Neighbors who have children but no pets: 0.25 × 0.65n = 0.1625n
Neighbors who have children and pets: 0.6 × 0.35n = 0.21n
Percent of neighbors who have children: 0.1625n + 0.21n = 0.3725n
37.25% of Mina’s neighbors have children.
Eureka Math Grade 7 Module 4 Lesson 16 Exit Ticket Answer Key
Question 1.
Jodie spent 25% less buying her English reading book than Claudia. Gianna spent 9% less than Claudia. Gianna spent more than Jodie by what percent?
Answer:
Let c represent the amount Claudia spent, in dollars. The number of dollars Jodie spent was 0.75c, and the number of dollars Gianna spent was 0.91c. 0.91c ÷ 0.75c = \(\frac{91}{75}\) × 100% = 121 \(\frac{1}{3}\)%. Gianna spent 21 \(\frac{1}{3}\)% more than Jodie.
Question 2.
Mr. Ellis is a teacher who tutors students after school. Of the students he tutors, 30% need help in computer science and the rest need assistance in math. Of the students who need help in computer science, 40% are enrolled in Mr. Ellis’s class during the school day. Of the students who need help in math, 25% are enrolled in his class during the school day. What percent of the after – school students are enrolled in Mr. Ellis’s classes?
Answer:
Let t represent the after – school students tutored by Mr. Ellis.
Computer science after – school students: 0.3t
Math after – school students: 0.7t
After – school computer science students who are also Mr. Ellis’s students: 0.4 × 0.3t = 0.12t
After – school math students who are also Mr. Ellis’s students: 0.25 × 0.7t = 0.175t
Number of after – school students who are enrolled in Mr. Ellis’s classes: 0.12t + 0.175t = 0.295t
Out of all the students Mr. Ellis tutors, 29.5% of the tutees are enrolled in his classes.