Engage NY Eureka Math 7th Grade Module 3 Lesson 11 Answer Key
Eureka Math Grade 7 Module 3 Lesson 11 Example Answer Key
Example 1.
The following figure shows three lines intersecting at a point. In a complete sentence, describe the angle relationship in the diagram. Write an equation for the angle relationship shown in the figure and solve for x. Confirm your answers by measuring the angle with a protractor.
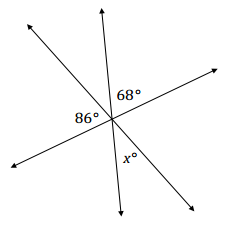
Answer:
The angles 86°, 68°, and the angle between them, which is vertically opposite and equal in measure to x, are angles on a line and have a sum of 180°.
86 + x + 68 = 180
x + 154 = 180
x + 154 – 154 = 180 – 154
x = 26
Example 2.
In a complete sentence, describe the angle relationships in the diagram. You may label the diagram to help describe the angle relationships. Write an equation for the angle relationship shown in the figure and solve for x. Confirm your answers by measuring the angle with a protractor.
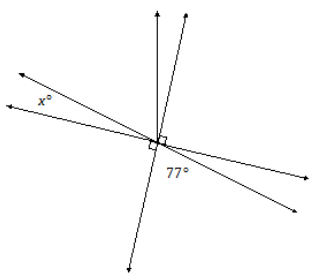
Answer:
The angle formed by adjacent angles a° and b° is vertically opposite to the 77° angle. The angles x°, a°, and b° are adjacent angles that have a sum of 90° (since the adjacent angle is a right angle and together the angles are on a line).
x + 77 = 90
x + 77 – 77 = 90 – 77
x = 13
Example 3.
In a complete sentence, describe the angle relationships in the diagram. Write an equation for the angle relationship shown in the figure and solve for x. Find the measures of ∠JAH and ∠GAF. Confirm your answers by measuring the angle with a protractor.
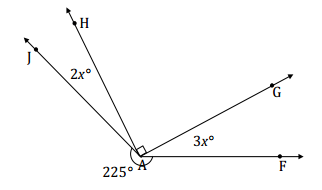
Answer:
The sum of the degree measurements of ∠JAH, ∠GAH, ∠GAF, and the arc that subtends ∠JAF is 360°.
225 + 2x + 90 + 3x = 360
315 + 5x = 360
315 – 315 + 5x = 360 – 315
5x = 45
(\(\frac{1}{5}\))5x = (\(\frac{1}{5}\))45
x = 9
m∠JAH = 2(9°) = 18° m∠GAF = 3(9°) = 27°
Example 4.
In the accompanying diagram, the measure of ∠DBE is four times the measure of ∠FBG.
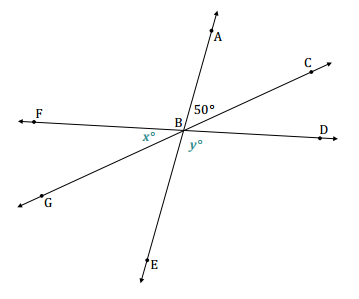
a. Label ∠DBE as y° and ∠FBG as x°. Write an equation that describes the relationship between ∠DBE and ∠FBG.
Answer:
y = 4x
b. Find the value of x.
Answer:
50 + x + 4x = 180
50 + 5x = 180
5x + 50 – 50 = 180 – 50
5x = 130
(\(\frac{1}{5}\))(5x) = (\(\frac{1}{5}\))(130)
x = 26
c. Find the measures of ∠FBG, ∠CBD, ∠ABF, ∠GBE, and ∠DBE.
Answer:
m∠FBG = 26°
m∠CBD = 26°
m∠ABF = 4(26°) = 104°
m∠GBE = 50°
m∠DBE = 104°
d. What is the measure of ∠ABG? Identify the angle relationship used to get your answer.
Answer:
∠ABG = ∠ABF + ∠FBG
∠ABG = 104 + 26
∠ABG = 130
m∠ABG = 130°
To determine the measure of ∠ABG, you need to add the measures of adjacent angles ∠ABF and ∠FBG.
Eureka Math Grade 7 Module 3 Lesson 11 Exercise Answer Key
Opening Exercise
a. In a complete sentence, describe the angle relationship in the diagram. Write an equation for the angle relationship shown in the figure and solve for x. Confirm your answers by measuring the angle with a protractor.
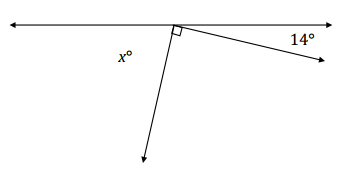
Answer:
The angles marked by x°, 90°, and 14° are angles on a line and have a sum of 180°.
x + 90 + 14 = 180
x + 104 = 180
x + 104 – 104 = 180 – 104
x = 76
b. \(\overleftrightarrow{C D}\) and \(\overleftrightarrow{E F}\) are intersecting lines. In a complete sentence, describe the angle relationship in the diagram. Write an equation for the angle relationship shown in the figure and solve for y. Confirm your answers by measuring the angle with a protractor.
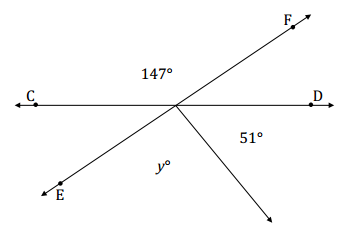
Answer:
The adjacent angles marked by y° and 51° together form the angle that is vertically opposite and equal to the angle measuring 147°.
y + 51 = 147
y + 51 – 51 = 147 – 51
y = 96
c. In a complete sentence, describe the angle relationship in the diagram. Write an equation for the angle relationship shown in the figure and solve for b. Confirm your answers by measuring the angle with a protractor.
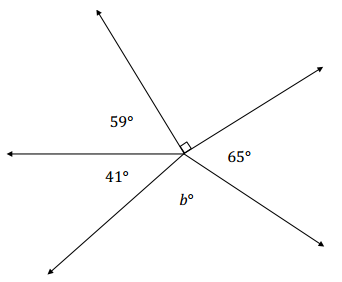
Answer:
The adjacent angles marked by 59°, 41°, b°, 65°, and 90° are angles at a point and together have a sum of 360°.
59 + 41 + b + 65 + 90 = 360
b + 255 = 360 – 255
b = 105
d. The following figure shows three lines intersecting at a point. In a complete sentence, describe the angle relationship in the diagram. Write an equation for the angle relationship shown in the figure and solve for z. Confirm your answers by measuring the angle with a protractor.
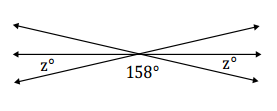
Answer:
The angles marked by z°, 158°, and z° are angles on a line and have a sum of 180°.
z + 158 + z = 180
2z + 158 = 180
2z + 158 – 158 = 180 – 158
2z = 22
z = 11
e. Write an equation for the angle relationship shown in the figure and solve for x. In a complete sentence, describe the angle relationship in the diagram. Find the measurements of ∠EPB and ∠CPA. Confirm your answers by measuring the angle with a protractor.
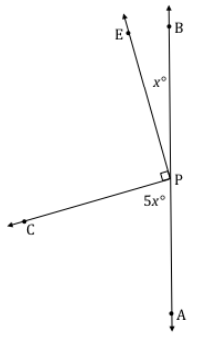
Answer:
∠CPA, ∠CPE, and ∠EPB are angles on a line and their measures have a sum of 180°.
5x + 90 + x = 180
6x + 90 = 180
6x + 90 – 90 = 180 – 90
6x = 90
(\(\frac{1}{6}\))6x = (\(\frac{1}{6}\))90
x = 15
∠EPB = 15°
∠CPA = 5(15°) = 75°
Exercise 1.
The following figure shows four lines intersecting at a point. In a complete sentence, describe the angle relationships in the diagram. Write an equation for the angle relationship shown in the figure and solve for x and y. Confirm your answers by measuring the angle with a protractor.
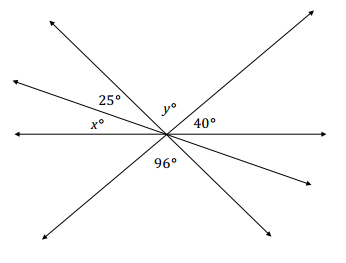
Answer:
The angles x°, 25°, y°, and 40° are angles on a line and have a sum of 180°; the angle marked y° is vertically opposite and equal to 96°.
y = 96, vert. ∠s
x + 25 + (96) + 40 = 180
x + 161 = 180
x + 161 – 161 = 180 – 161
x = 19
Exercise 2.
In a complete sentence, describe the angle relationships in the diagram. Write an equation for the angle relationship shown in the figure and solve for x and y. Confirm your answers by measuring the angles with a protractor.
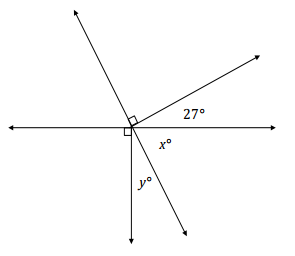
Answer:
The measures of angles x and y have a sum of 90°; the measures of angles x and 27 have a sum of 90°.
x + 27 = 90
x + 27 – 27 = 90 – 27
x = 63
(63) + y = 90
63 – 63 + y = 90 – 63
y = 27
Exercise 3.
In a complete sentence, describe the angle relationships in the diagram. Write an equation for the angle relationship shown in the figure and solve for x. Find the measure of ∠JKG. Confirm your answer by measuring the angle with a protractor.
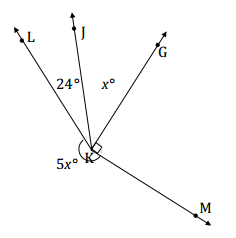
Answer:
The sum of the degree measurements of ∠LKJ, ∠JKG, ∠GKM, and the arc that subtends ∠LKM is 360°.
5x + 24 + x + 90 = 360
6x + 114 = 360
6x + 114 – 114 = 360 – 114
6x = 246
(\(\frac{1}{6}\))6x = (\(\frac{1}{6}\))246
x = 41
m∠JKG = 41°
Eureka Math Grade 7 Module 3 Lesson 11 Problem Set Answer Key
In a complete sentence, describe the angle relationships in each diagram. Write an equation for the angle relationship(s) shown in the figure, and solve for the indicated unknown angle. You can check your answers by measuring each angle with a protractor.
Question 1.
Find the measures of ∠EAF, ∠DAE, and ∠CAD.
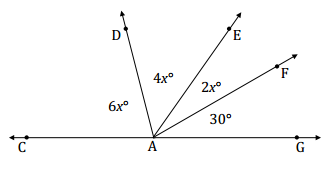
Answer:
∠GAF, ∠EAF, ∠DAE, and ∠CAD are angles on a line and their measures have a sum of 180°.
6x + 4x + 2x + 30 = 180
12x + 30 = 180
12x + 30 – 30 = 180 – 30
12x = 150
x = 12.5
m∠EAF = 2(12.5°) = 25°
m∠DAE = 4(12.5°) = 50°
m∠CAD = 6(12.5°) = 75°
Question 2.
Find the measure of a.
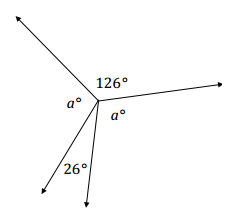
Answer:
Angles a°, 26°, a°, and 126° are angles at a point and have a sum of 360°.
a + 126 + a + 26 = 360
2a + 152 = 360
2a + 152 – 152 = 360 – 152
2a = 208
(\(\frac{1}{2}\))2a = (\(\frac{1}{2}\))208
a = 104
Question 3.
Find the measures of x and y.
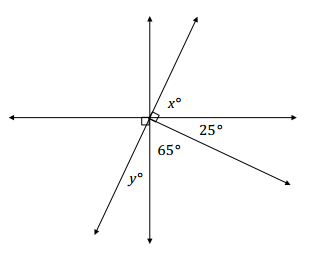
Answer:
Angles y° and 65° and angles 25° and x° have a sum of 90°.
x + 25 = 90
x + 25 – 25 = 90 – 25
x = 65
65 + y = 90
65 + y = 90
65 – 65 + y = 90 – 65
y = 25
Question 4.
Find the measure of ∠HAJ.
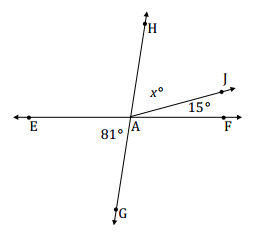
Answer:
Adjacent angles x° and 15° together are vertically opposite from and are equal to angle 81°.
x + 15 = 81
x + 15 – 15 = 81 – 15
x = 66
m∠HAJ = 66°
Question 5.
Find the measures of ∠HAB and ∠CAB.
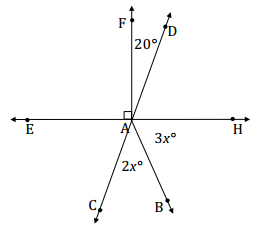
Answer:
The measures of adjacent angles ∠CAB and ∠HAB have a sum of the measure of ∠CAH, which is vertically opposite from and equal to the measurement of ∠DAE.
2x + 3x + 70 = 180
5x = 110
(\(\frac{1}{5}\))5x = (\(\frac{1}{5}\))110
x = 22
m∠HAB = 3(22°) = 66°
m∠CAB = 2(22°) = 44°
Question 6.
The measure of ∠SPT is b°. The measure of ∠TPR is five more than two times ∠SPT. The measure of ∠QPS is twelve less than eight times the measure of ∠SPT. Find the measures of ∠SPT, ∠TPR, and ∠QPS.
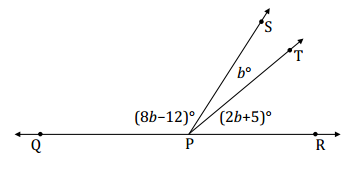
Answer:
∠QPS, ∠SPT, and ∠TPR are angles on a line and their measures have a sum of 180°.
(8b – 12) + b + (2b + 5) = 180
11b – 7 = 180
11b – 7 + 7 = 180 + 7
11b = 187
(\(\frac{1}{11}\))11b = (\(\frac{1}{11}\))187
b = 17
m∠SPT = (17°) = 17°
m∠TPR = 2(17°) + 5° = 39°
m∠QPS = 8(17°) – 12° = 124°
Question 7.
Find the measures of ∠HQE and ∠AQG.
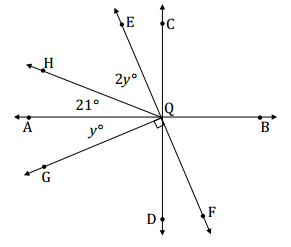
Answer:
∠AQG, ∠AQH, and ∠HQE are adjacent angles whose measures have a sum of 90°.
2y + 21 + y = 90
3y + 21 = 90
3y + 21 – 21 = 90 – 21
3y = 69
(\(\frac{1}{3}\))3y = (\(\frac{1}{3}\))69
y = 23
m∠HQE = 2(23°) = 46°
m∠AQG = (23°) = 23°
Question 8.
The measures of three angles at a point are in the ratio of 2:3:5. Find the measures of the angles.
Answer:
∠A = 2x, ∠B = 3x, ∠C = 5x
2x + 3x + 5x = 360
10x = 360
(\(\frac{1}{10}\))10x = (\(\frac{1}{10}\))360
x = 36
∠A = 2(36°) = 72°
∠B = 3(36°) = 108°
∠C = 5(36°) = 180°
Question 9.
The sum of the measures of two adjacent angles is 72°. The ratio of the smaller angle to the larger angle is 1∶3. Find the measures of each angle.
Answer:
∠A = x, ∠B = 3x
x + 3x = 72
4x = 72
(\(\frac{1}{4}\))(4x) = (\(\frac{1}{4}\))(72)
x = 18
∠A = (18°) = 18°
∠B = 3(18°) = 54°
Question 10.
Find the measures of ∠CQA and ∠EQB.
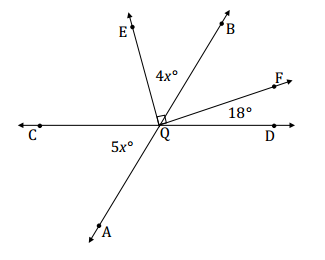
Answer:
4x + 5x = 108
9x = 108
(\(\frac{1}{9}\))9x = (\(\frac{1}{9}\))108
x = 12
m∠CQA = 5(12°) = 60°
m∠EQB = 4(12°) = 48°
Eureka Math Grade 7 Module 3 Lesson 11 Exit Ticket Answer Key
Question 1.
Write an equation for the angle relationship shown in the figure and solve for x. Find the measures of ∠RQS and ∠TQU.
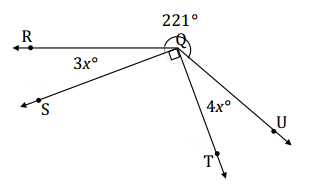
Answer:
3x + 90 + 4x + 221 = 360
7x + 311 = 360
7x + 311 – 311 = 360 – 311
7x = 49
(\(\frac{1}{7}\))7x = (\(\frac{1}{7}\))49
x = 7
m∠RQS = 3(7°) = 21°
m∠TQU = 4(7°) = 28°