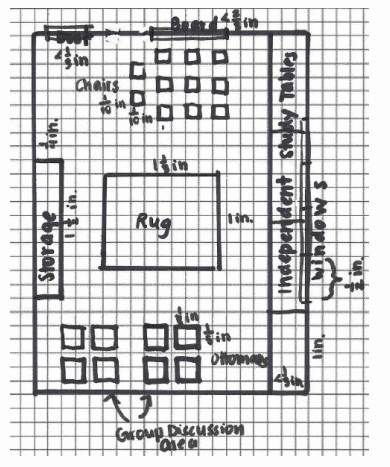
Engage NY Eureka Math 7th Grade Module 1 Lesson 21 Answer Key
Eureka Math Grade 7 Module 1 Lesson 21 Exploratory Challenge Answer Key
Exploratory Challenge: A New Scale Factor
The school plans to publish your work on the dream classroom in the next newsletter. Unfortunately, in order to fit the drawing on the page in the magazine, it must be \(\frac{1}{4}\) its current length. Create a new drawing (SD2) in which all of the lengths are \(\frac{1}{4}\) those in the original scale drawing (SD1) from Lesson 20.

Answer:
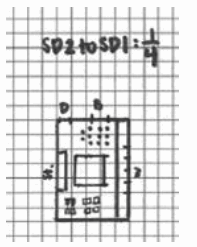
An example is included for students unable to create SD1 at the end of Lesson 20. Pose the following questions:
→ Would the new scale create a larger or smaller scale drawing as compared to the original drawing?
→ It would be smaller because \(\frac{1}{4}\) is smaller than one.
→ How would you use the scale factor between SD1 to SD2 to calculate the new scale drawing lengths without having to get the actual measurement first?
→ Take the original scale drawing lengths and multiply them by \(\frac{1}{4}\) to find the new scale lengths.
→ Once students have finished creating SD2, ask students to prove to the architect that SD2 is actually a scale drawing of the original room.
→ How can we go about proving that the new scale drawing (SD2) is actually a scale drawing of the original room?
→ The scale lengths of SD2 have to be proportional to the actual lengths. We need to find the constant of proportionality, the scale factor.
How do we find the new scale factor?
→ Divide one of the new scale lengths by its corresponding actual length.
→ If the actual measurement was not known, how could we find it?
→ Calculate the actual length by using the scale factor on the original drawing. Multiply the scale length of the original drawing by the original scale factor.
Eureka Math Grade 7 Module 1 Lesson 21 Exercise Answer Key
The picture shows an enlargement or reduction of a scale drawing of a trapezoid.
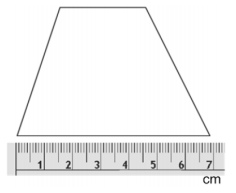
Using the scale factor written on the card you chose, draw your new scale drawing with correctly calculated measurements.
Answers may vary depending on the card. One sample response could be, 1 cm, 1\(\frac{5}{6}\) cm, 2 \(\frac{1}{3}\) cm, 1 \(\frac{2}{3}\) cm.
a. What is the scale factor between the original scale drawing and the one you drew?
Answer:
\(\frac{1}{3}\)
b. The longest base length of the actual trapezoid is 10 cm. What is the scale factor between the original scale drawing and the actual trapezoid?
Answer:
\(\frac{7}{10}\)
c. What is the scale factor between the new scale drawing you drew and the actual trapezoid?
Answer:
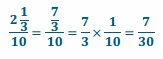
Eureka Math Grade 7 Module 1 Lesson 21 Problem Set Answer Key
Question 1.
Jake reads the following problem: If the original scale factor for a scale drawing of a square swimming pool is \(\frac{1}{90}\), and the length of the original drawing measured to be 8 inches, what is the length on the new scale drawing if the scale factor of the new scale drawing length to actual length is \(\frac{1}{144}\)?
He works out the problem:
8 inches ÷ \(\frac{1}{90}\) = 720 inches
720 inches × \(\frac{1}{144}\) = 5 inches
Is he correct? Explain why or why not.
Answer:
Jake is correct. He took the original scale drawing length and divided by the original scale factor to get the actual length, 720 inches. To get the new scale drawing length, he takes the actual length, 720, and multiplies by the new scale factor, \(\frac{1}{144}\), to get 5 inches.
Question 2.
What is the scale factor of the new scale drawing to the original scale drawing (SD2 to SD1)?
Answer:
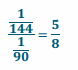
Question 3.
Using the scale, if the length of the pool measures 10 cm on the new scale drawing:
a. Using the scale factor from Problem 1, \(\frac{1}{144}\), find the actual length of the pool in meters.
Answer:
14.40 m
b. What is the surface area of the floor of the actual pool? Rounded to the nearest tenth.
Answer:
14.4 m × 14.4 m
207.36 m2 ≈ 207.4 m2
c. If the pool has a constant depth of 1.5 meters, what is the volume of the pool? Rounded to the nearest tenth.
Answer:
14.4 m × 14.4 m × 1.5 m
311.04 m3 ≈ 311.0 m3
d. If 1 cubic meter of water is equal to 264.2 gallons, how much water will the pool contain when completely filled? Rounded to the nearest unit.
Answer:
311.0 m3 × \(\frac{264.2 \text { gallons }}{1 \mathrm{~m}^{3}}\)
82,166.2 gallons
Question 4.
Complete a new scale drawing of your dream room from the Problem Set in Lesson 20 by either reducing by \(\frac{1}{4}\) or enlarging it by 4.
Answer:
Scale drawings will vary.
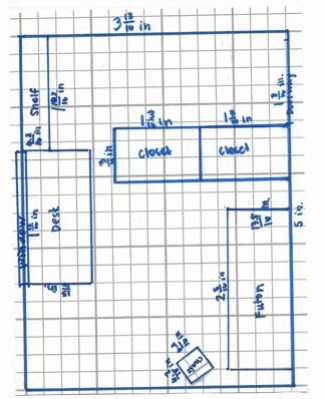
SD1 Example for students who were unable to create their own from Lesson 20
SCALE FACTOR:
\(\frac{1}{120}\)