Engage NY Eureka Math 6th Grade Module 3 Lesson 5 Answer Key
Eureka Math Grade 6 Module 3 Lesson 5 Opening Exercise Answer Key
a. Locate the number – 2 and its opposite on the number line below.
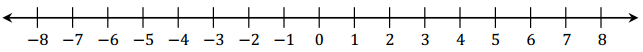
Answer:

b. Write an integer that represents each of the following.
i. 90 feet below sea level
Answer:
– 90
ii. $100 of debt
Answer:
– 100
iii. 2°C above zero
Answer:
2
c. Joe is at the Ice cream shop, and his house is 10 blocks north of the shop. The park is 10 blocks south of the ice cream shop. When he is at the ice cream shop, is Joe closer to the park or his house? How could the number zero be used in this situation? Explain.
Answer:
He is the same distance from his house and the park because both are located 10 blocks away from the ice cream shop but in opposite directions. In this situation, zero represents the locution of the ice cream shop.
Eureka Math Grade 6 Module 3 Lesson 5 Example Answer Key
Example 1:
The Opposite of an Opposite of a Number
What is the opposite of the opposite of 8? How can we illustrate this number on a number line?
a. What number is 8 unIts to the right of 0?
Answer:
8
b. How can you illustrate locating the opposite of 8 on this number line?
Answer:
We can illustrate the opposite of 8 on the number line by counting 8 units to the left of zero rather than to the right of zero.
c. What is the opposite of 8?
Answer:
– 8
d. Use the same process to locate the opposite of – 8. What is the opposite of – 8? _________
![]()
Answer:
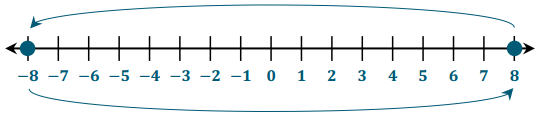
e. The opposite of an opposite of a number is
Answer:
the original number
Eureka Math Grade 6 Module 3 Lesson 5 Exercise Answer Key
Complete the table using the cards in your group.

Answer:

Question 1.
Write the opposite of the opposite of – 10 as an equation.
Answer:
The opposite of – 10: – (- 10) = 10; the opposite of 10: – (10) = – 10. Therefore,(- ( – (- 10))) = – 10.
Question 2.
In general, the opposite of the opposite of a number is the
Answer:
original number.
Question 3.
Provide a real-world example of this rule. Show your work.
Answer:
Answers will vary. The opposite of the opposite of 100 feet below sea level is 100 feet below sea level.
– 100 is 100 feet below sea level.
– (- 100) = 100, the opposite of – 100
– (100) = – 100, the opposite of 100
Eureka Math Grade 6 Module 3 Lesson 5 Problem Set Answer Key
Question 1.
Read each description carefully, and write an equation that represents the description.
a. The opposite of negative seven
Answer:
– (- 7) = 7
b. The opposite of the opposite of twenty-five
Answer:
– (- (25)) = – 25
c. The opposite of fifteen
Answer:
– (15) = – 15
d. The opposite of negative thirty-six
Answer:
– (- 36) = – 36
Question 2.
Jose graphed the opposite of the opposite of 3 on the number line. First, he graphed point P on the number line 3 units to the right of zero. Next, he graphed the opposite of P on the number line 3 units to the left of zero and labeled it K. Finally, he graphed the opposite of K and labeled it Q.

a. Is his diagram correct? Explain. If the diagram Is not correct, explain his error, and correctly locate and label point Q.
Answer:
Yes, his diagram is correct. It shows that point P is 3 because It is 3 units to the right of zero. The opposite of 3 is – 3, which is point K (3 units to the left of zero). The opposite of – 3 is 3, so point Q is 3 units to the right of zero.
b. Write the relationship between the points:
P and K
Answer:
They are opposites.
K and Q
Answer:
They are opposites.
P and Q
Answer:
They are the same.
Question 3.
Read each real-world description. Write the integer that represents the opposite of the opposite. Show your work to support your answer.
a. A temperature rise of 15 degrees Fahrenheit
Answer:
– 15 is the opposite of 15 (fall in temperature).
15 is the opposite of – 15 (rise in temperature).
– (- (15)) = 15
b. A gain of 55 yards
Answer:
– 55 is the opposite of 55 (loss of yards).
55 is the opposite of – 55 (gain of yards).
– (- (55)) = 55
c. A loss of 10 pounds
Answer:
10 is the opposite of – 10 (gain of pounds).
– 10 is the opposite of 10 (loss of pounds).
– (- (- 10)) = – 10
d. A withdrawal of $2,000
Answer:
2,000 is the opposite of – 2,000 (deposit).
– 2,000 is the opposite of 2,000 (withdrawal).
– (- (- 2,000)) = – 2,000
Question 4.
Write the integer that represents the statement. Locate and label each point on the number line below.
Answer:
a. The opposite of a gain of 6
Answer:
– 6
b. The opposite of a deposit of $10
Answer:
– 10
c. The opposite of the opposite of 0
Answer:
0
d. The opposite of the opposite of 4
Answer:
4
e. The opposite of the opposite of a loss of 5
Answer:
– 5

Eureka Math Grade 6 Module 3 Lesson 5 Exit Ticket Answer Key
Question 1.
Jane completes several example problems that ask her to the find the opposite of the opposite of a number, and for each example, the result is a positive number. Jane concludes that when she takes the opposite of the opposite of any number, the result will always be positive. Is Jane correct? Why or why not?
Answer:
She is not correct. The opposite of the opposite of a number is the original number. So, if Jane starts with a negative number, she will end with a negative number.
Question 2.
To support your answer from the previous question, create an example, written as an equation. Illustrate your example on the number line below.
Answer:
If Jane starts with – 7, the opposite of the opposite of – 7 is written as – (- (- 7)) = – 7 or the opposite of – 7:
– (- 7) = 7; the opposite of 7: – (7) = – 7.
![]()
Answer:
