Engage NY Eureka Math 5th Grade Module 6 Lesson 6 Answer Key
Eureka Math Grade 5 Module 6 Lesson 6 Problem Set Answer Key
Question 1.
Plot the following points, and label them on the coordinate plane.
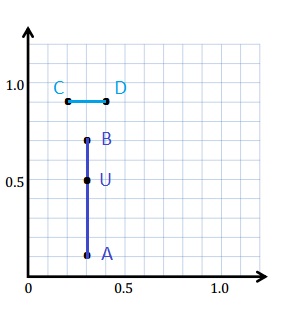
A: (0.3, 0.1)
B: (0.3, 0.7)
C: (0.2, 0.9)
D: (0.4, 0.9)
a. Use a straightedge to construct line segments \(\overline{A B}\) and \(\overline{C D}\).
b. Line segment _________ is parallel to the x-axis and is perpendicular to the y-axis.
c. Line segment _________ is parallel to the y-axis and is perpendicular to the x-axis.
d. Plot a point on line segment \(\overline{A B}\) that is not at the endpoints, and name it U. Write the coordinates. U ( _____ , _____ )
e. Plot a point on line segment \(\overline{C D}\) and name it V. Write the coordinates. V ( _____ , _____ )
Answer:
a.

b. Line segment \(\overline{C D}\) is parallel to the x-axis and is perpendicular to the y-axis.
c. Line segment \(\overline{A B}\) is parallel to the y-axis and is perpendicular to the x-axis.
d. The coordinates. U ( 0.3 , 0.5 )
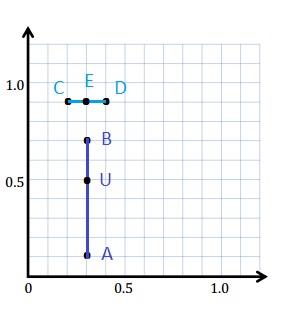
e. The coordinates. V ( 0.3 , 0.9 )
Question 2.
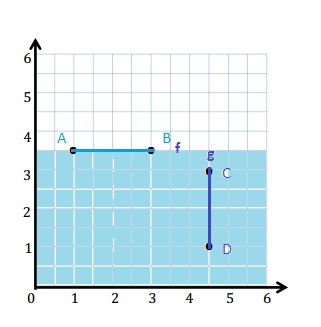
Construct line f such that the y-coordinate of every point is 3\(\frac{1}{2}\), and construct line g such that the x-coordinate of every point is 4\(\frac{1}{2}\).

a. Line f is ________ units from the x-axis.
b. Give the coordinates of the point on line f that is \(\frac{1}{2}\) unit from the y-axis. ________
c. With a blue pencil, shade the portion of the grid that is less than 3\(\frac{1}{2}\) units from the x-axis.
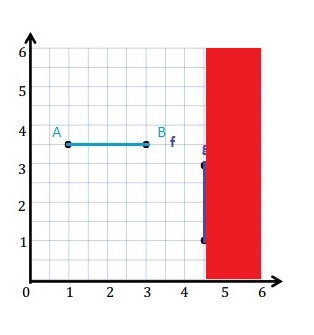
d. Line g is _________ units from the y-axis.
e. Give the coordinates of the point on line g that is 5 units from the x-axis. ________
f. With a red pencil, shade the portion of the grid that is more than 4\(\frac{1}{2}\) units from the y-axis.
Answer:
Line f is drawn with points A and B with the y-coordinate of every point is 3\(\frac{1}{2}\) .
A : (1, 3\(\frac{1}{2}\))
B : (3, 3\(\frac{1}{2}\))
Line g is drawn with points C and D with the x-coordinate of every point is 4\(\frac{1}{2}\) .
C : (4\(\frac{1}{2}\) , 3 )
D : ( 4\(\frac{1}{2}\) , 1)
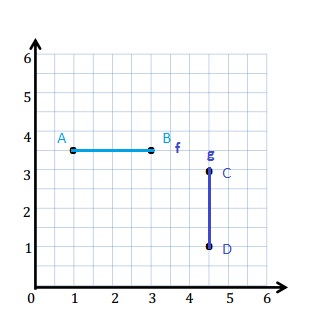
a. Line f is 4\(\frac{1}{2}\) units from the x-axis.
Explanation :
Distance between f and x-axis is the y-coordinate .
b. The coordinate of the point is ( \(\frac{1}{2}\) , 3\(\frac{1}{2}\) )
c.
d. Line g is 4\(\frac{1}{2}\) units from the y-axis.
Explanation :
Distance between g and y-axis is the x-coordinate .
e. The coordinates of the point on line g that is 5 units from the x-axis is ( 4\(\frac{1}{2}\) , 5 )
f.
Question 3.
Complete the following tasks on the plane below.
a. Construct a line m that is perpendicular to the x-axis and 3.2 units from the y-axis.
b. Construct a line a that is 0.8 unit from the x-axis.
c. Construct a line t that is parallel to line m and is halfway between line m and the y-axis.
d. Construct a line h that is perpendicular to line t and passes through the point (1.2, 2.4).
e. Using a blue pencil, shade the region that contains points that are more than 1.6 units and less than 3.2 units from the y-axis.
f. Using a red pencil, shade the region that contains points that are more than 0.8 unit and less than 2.4 units from the x-axis.
g. Give the coordinates of a point that lies in the double-shaded region.
Answer:

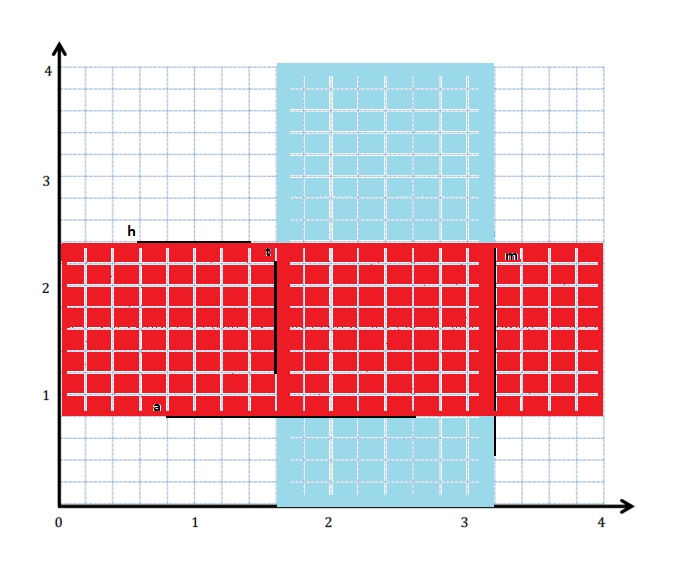
g. The coordinates of a point that lies in the double-shaded region is (1, 2)
Eureka Math Grade 5 Module 6 Lesson 6 Exit Ticket Answer Key

Question 1.
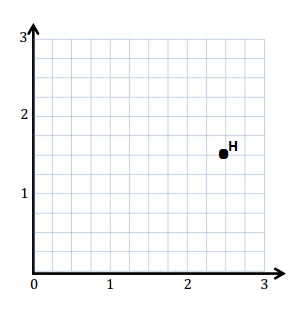
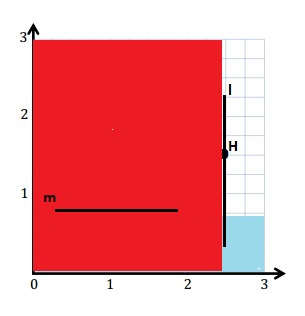
Plot the point H (2\(\frac{1}{2}\), 1\(\frac{1}{2}\)).
Answer:
Question 2.
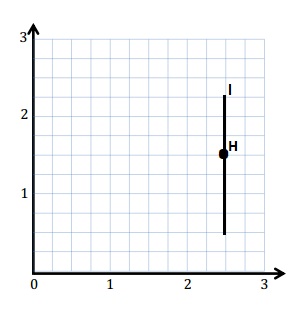
Line l passes through point H and is parallel to the y-axis. Construct line l.
Answer:
Question 3.
Construct line m such that the y-coordinate of every point is \(\frac{3}{4}\).
Answer:
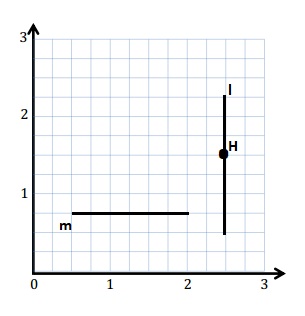
Explanation :
For same y -coordinate of every point is \(\frac{3}{4}\) then draw a line from \(\frac{3}{4}\) from x-axis .
Question 4.
Line m is ________ units from the x-axis.
Answer:
Line m is \(\frac{3}{4}\) units from the x-axis.
Explanation :
It is represented by y-coordinate of line m .
Question 5.
Give the coordinates of the point on line m that is \(\frac{1}{2}\) unit from the y-axis.
Answer:
The coordinates of the point on line m that is \(\frac{1}{2}\) unit from the y-axis is (\(\frac{1}{2}\) , \(\frac{3}{4}\) ).
Question 6.
With a blue pencil, shade the portion of the plane that is less than \(\frac{3}{4}\) unit from the x-axis.
Answer:
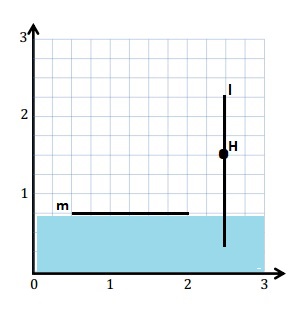
Question 7.
With a red pencil, shade the portion of the plane that is less than 2\(\frac{1}{2}\) units from the y-axis.
Answer:
Question 8.
Plot a point that lies in the double-shaded region. Give the coordinates of the point.
Answer:
The point that lies in the double-shaded region is W ( 2 , \(\frac{1}{2}\) )

Eureka Math Grade 5 Module 6 Lesson 6 Homework Answer Key
Question 1.
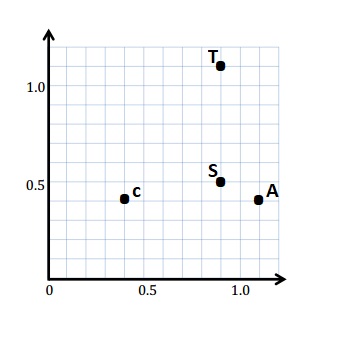
Plot and label the following points on the coordinate plane.
C: (0.4, 0.4)
A: (1.1, 0.4)
S: (0.9, 0.5)
T: (0.9, 1.1)
a. Use a straightedge to construct line segments \(\overline{C A}\) and \(\overline{S T}\).
b. Name the line segment that is perpendicular to the x-axis and parallel to the y-axis. _________
c. Name the line segment that is parallel to the x-axis and perpendicular to the y-axis. _________
d. Plot a point on \(\overline{C A}\), and name it E. Plot a point on line segment \(\overline{S T}\), and name it R.
e. Write the coordinates of points E and R.
E ( ____ , ____ ) R ( ____ , ____ )
Answer:
a.
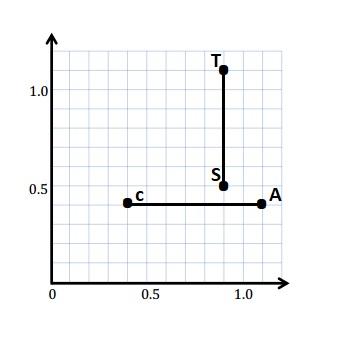
c. The line segment that is perpendicular to the x-axis and parallel to the y-axis is \(\overline{S T}\)
d. The line segment that is parallel to the x-axis and perpendicular to the y-axis is \(\overline{C A}\)
e.
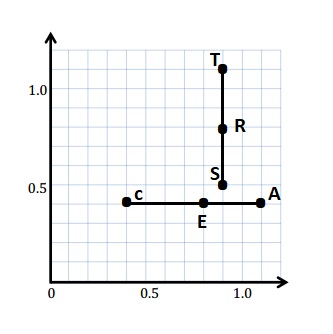
f. The coordinates of points E and R.
E ( 0.8 , 0.4 ) R ( 0.9 , 0.8 )
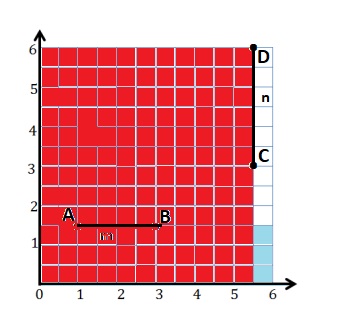
Question 2.
Construct line m such that the y-coordinate of every point is 1\(\frac{1}{2}\), and construct line n such that the x-coordinate of every point is 5\(\frac{1}{2}\).
a. Line m is ________ units from the x-axis.
b. Give the coordinates of the point on line m that is 2 units from the y-axis. ________
c. With a blue pencil, shade the portion of the grid that is less than 1\(\frac{1}{2}\) units from the x-axis.
d. Line n is _________ units from the y-axis.
e. Give the coordinates of the point on line n that is 3\(\frac{1}{2}\) units from the x-axis.
f. With a red pencil, shade the portion of the grid that is less than 5\(\frac{1}{2}\) units from the y-axis.
Answer:
Line m is drawn with points A and B with the y-coordinate of every point is 1\(\frac{1}{2}\) .
A : (1, 1\(\frac{1}{2}\))
B : (3, 1\(\frac{1}{2}\))
Line n is drawn with points C and D with the x-coordinate of every point is 5\(\frac{1}{2}\) .
C : (5\(\frac{1}{2}\) , 3 )
D : ( 5\(\frac{1}{2}\) , 6)
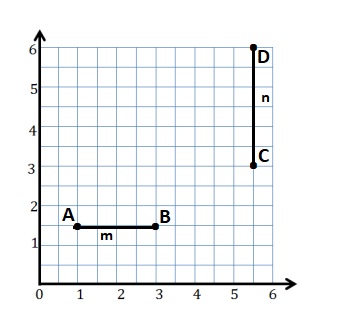
a. a. Line m is 1\(\frac{1}{2}\) units from the x-axis.
Explanation :
Distance between x-axis and line m is the y coordinate .
b. The coordinates of the point on line m that is 2 units from the y-axis is ( 2, 1\(\frac{1}{2}\) )
c.
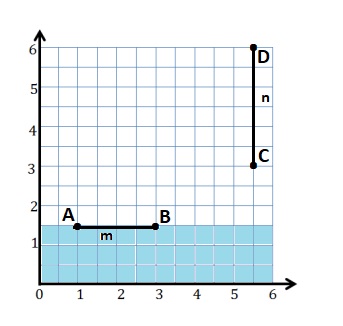
d. Line n is 5\(\frac{1}{2}\) units from the y-axis.
Explanation :
Explanation :
Distance between y-axis and line n is the x – coordinate .
e. The coordinates of the point on line n that is 3\(\frac{1}{2}\) units from the x-axis is (5\(\frac{1}{2}\) , 3\(\frac{1}{2}\))
f.
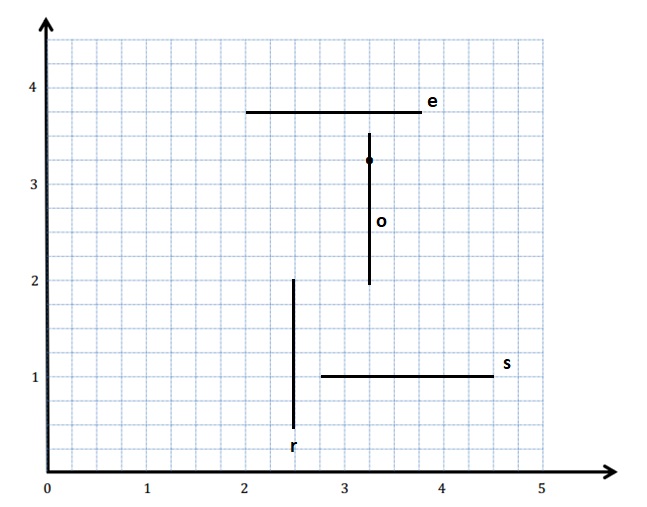
Question 3.
Construct and label lines e, r, s, and o on the plane below.
a. Line e is 3.75 units above the x-axis.
b. Line r is 2.5 units from the y-axis.
c. Line s is parallel to line e but 0.75 farther from the x-axis.
d. Line o is perpendicular to lines s and e and passes through the point (3\(\frac{1}{4}\), 3\(\frac{1}{4}\)).
Answer:
Question 4.
Complete the following tasks on the plane.
a. Using a blue pencil, shade the region that contains points that are more than 2\(\frac{1}{2}\) units and less than 3\(\frac{1}{4}\) units from the y-axis.
b. Using a red pencil, shade the region that contains points that are more than 3\(\frac{3}{4}\) units and less than 4\(\frac{1}{2}\) units from the x-axis.
c. Plot a point that lies in the double-shaded region, and label its coordinates.
Answer:

Explanation :
In double shaded (3,4 ) is a point that is marked as shown in above figure .