Engage NY Eureka Math 4th Grade Module 3 Lesson 2 Answer Key
Eureka Math Grade 4 Module 3 Lesson 2 Problem Set Answer Key
Question 1.
A rectangular porch is 4 feet wide. It is 3 times as long as it is wide.
a. Label the diagram with the dimensions of the porch.

Answer:
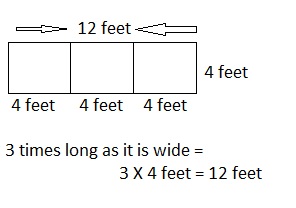
Explanation:
Given a rectangular porch is 4 feet wide.
It is 3 times as long as it is wide.
Labeled the diagram with the dimensions of the porch as
shown above, width= 4 feet and long = 3 × 4 feet = 12 feet
or 4 feet + 4 feet + 4 feet = 12 feet respectively.
b. Find the perimeter of the porch.
Answer:
Perimeter of the porch is 32 feet,
Explanation:
Given width = 4 feet and long is 12 feet, so perimeter
of rectangular porch is 2 × ( 12 feet + 4 feet) =
2 × (16 feet) = 32 feet.
Question 2.
A narrow rectangular banner is 5 inches wide. It is 6 times as long as it is wide.
a. Draw a diagram of the banner, and label its dimensions.
Answer:
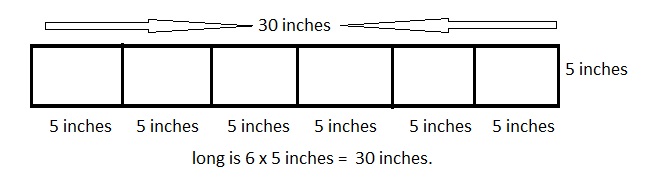
Explanation:
Drawn a diagram of the banner, and labeled its dimensions
as shown above wide 5 inches and long is 6 x 5 inches =
30 inches.
b. Find the perimeter and area of the banner.
Answer:
Perimeter of the banner : 70 inches,
Area of the banner : 150 inches2,
Explanation:
Given a narrow rectangular banner is 5 inches wide.
It is 6 times as long as it is wide. So wide = 5 inches,
long = 6 X 5 inches = 30 inches,
Perimeter of the banner = 2 X (l + w) = 2 X (30 inches + 5 inches) =
2 X ( 35 inches) = 70 inches and area of the banner = l X w =
30 inches X 5 inches = 150 square inches.
Question 3.
The area of a rectangle is 42 square centimeters. Its length is 7 centimeters.
a. What is the width of the rectangle?
Answer:
The width of the rectangle is 6 centimeters,
Explanation:
Given The area of a rectangle is 42 square centimeters.
Its length is 7 centimeters. So let us take width as x cm,
so 42 sq cm = 7 cm X x cm, x cm = 42 sq cm X cm ÷ 7 cm = 6 cm,
therefore, the width of the rectangle is 6 centimeters.
b. Charlie wants to draw a second rectangle that is the same length but is 3 times as wide. Draw and label Charlie’s second rectangle.
Answer:
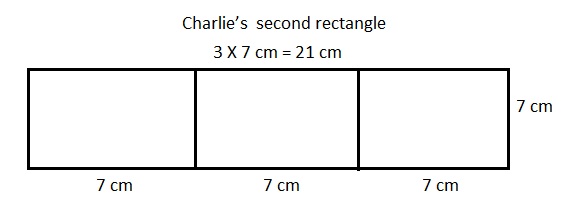
Explanation:
Given Charlie wants to draw a second rectangle that is the same length but is 3 times as wide means length is 7 cm and wide is 3 × 7 cm = 21 cm, Drawn and labeled Charlie’s second rectangle as shown above.
c. What is the perimeter of Charlie’s second rectangle?
Answer:
Perimeter of Charlie’s second rectangle is 56 centimeters,
Explanation:
Given Charlie’s second rectangle has length 7 cm and width as 21 cm
so perimeter is 2 X ( 7 cm + 21 cm) =
2 × (28 cm) = 56 cm, therefore perimeter of Charlie’s second rectangle is 56 centimeters.
Question 4.
The area of Betsy’s rectangular sandbox is 20 square feet. The longer side measures 5 feet. The sandbox at the park is twice as long and twice as wide as Betsy’s.
a. Draw and label a diagram of Betsy’s sandbox. What is its perimeter?
Answer:
Perimeter of Betsy’s sandbox is 18 feet,
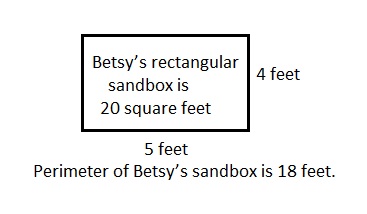
Explanation:
Given the area of Betsy’s rectangular sandbox is 20 square feet. The longer side measures 5 feet.
Drawn and labeled a diagram of Betsy’s sandbox as shown above and the its perimeter is as area = 20 square feet, lets take width as x feet so x feet = 20 feet × feet ÷ 5 feet = 4 feet,
now perimeter = 2 × ( 5 feet + 4 feet) = 2 X 9 feet = 18 feet,
therefore, the Perimeter of Betsy’s sandbox is 18 feet.
b. Draw and label a diagram of the sandbox at the park.
What is its perimeter?
Answer:
The perimeter of the sand box at park is 36 feet,

Explanation:
Given the sandbox at the park is twice as long and twice as wide as Betsy’s means long is 5 feet + 5 feet = 10 feet and wide is 4 feet + 4 feet = 8 feet,
Now draw and label a diagram of the sandbox at the park.
The perimeter of sandbox at the park is 2 × (10 feet + 8 feet) = 2 × 18 feet = 36 feet.
c. What is the relationship between the two perimeters?
Answer:
The perimeter of sandbox at the park is twice the perimeter of Betsy’s sandbox,
Explanation:
As both length and width of sandbox at park is twice of Betsy’s sandbox, so their perimeter of sandbox at park is twice the perimeter of Betsy’s sandbox.
d. Find the area of the park’s sandbox using the formula A = l × w.
Answer:
Area of the park’s sandbox is 80 square feet,
Explanation:
As sandbox at park has 10 feet long and 8 feet wide so area of sandbox at park is 10 feet X 8 feet = 80 square feet.
e. The sandbox at the park has an area that is how many times that of Betsy’s sandbox?
Answer:
The sandbox at the park has an area that is four times that of Betsy’s sandbox,
Explanation:
Given area of Betsy’s rectangular sandbox is 20 square feet and area of the park’s sandbox is 80 square feet,
so number of times more is 80 square feet ÷ 20 square feet = 4,
therefore the sandbox at the park has an area that is four times that of Betsy’s sandbox.
f. Compare how the perimeter changed with how the area changed between the two sandboxes. Explain what you notice using words, pictures, or numbers.
Answer:
Sand box at park has twice perimeter and area has became four times that of Betsy’s sandbox,
Explanation:
As we know Perimeter of Betsy’s sandbox is 18 feet and perimeter of the sand box at park is 36 feet,
Area of Betsy’s rectangular sandbox is 20 square feet and area of the park’s sandbox is 80 square feet, Now on comparing
Sand box at park has twice perimeter and area has became four times to that of Betsy’s sandbox.
Eureka Math Grade 4 Module 3 Lesson 2 Exit Ticket Answer Key
Question 1.
A table is 2 feet wide. It is 6 times as long as it is wide.
a. Label the diagram with the dimensions of the table.

Answer:

Explanation:
Labeled the diagram with the dimensions of the table as shown above, wide= 2 feet and long is 6 X 2 feet = 12 feet.
b. Find the perimeter of the table.
Answer:
Perimeter of the table is 28 feet,
Explanation:
Given wide is 2 feet and long is 12 feet,
So Perimeter of the table is 2 × ( 12 feet + 2 feet) = 2 × 14 feet = 28 feet.
Question 2.
A blanket is 4 feet wide. It is 3 times as long as it is wide.
a. Draw a diagram of the blanket, and label its dimensions.
Answer:

Explanation:
Labeled the diagram of the blanket with the dimensions as shown above, wide= 4 feet and long is 3 X 4 feet = 12 feet.
b. Find the perimeter and area of the blanket.
Answer:
Perimeter is 32 feet and area of the blanket is 48 square feet,
Explanation:
Given wide as 4 feet and long is 12 feet, So perimeter of the blanket is 2 × (12 feet + 4 feet) = 2 × (16 feet) = 32 feet and
area is 12 feet × 4 feet = 48 square feet.
Eureka Math Grade 4 Module 3 Lesson 2 Homework Answer Key
Question 1.
A rectangular pool is 7 feet wide. It is 3 times as long as it is wide.
a. Label the diagram with the dimensions of the pool.
Answer:
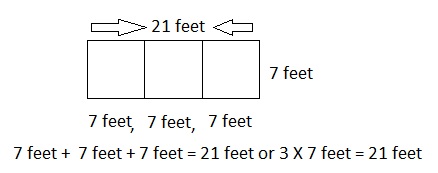
Explanation:
Labeled the diagram of the rectangular pool with the dimensions as shown above, wide= 7 feet and long is 3 X 7 feet = 21 feet.
b. Find the perimeter of the pool.
Answer:
Perimeter of the rectangular pool is 56 feet,
Explanation:
Given rectangular pool is 7 feet wide and 21 feet long,
So perimeter is 2 X (21 feet + 7 feet) = 2 X 28 feet = 56 feet.
Question 2.
A poster is 3 inches long. It is 4 times as wide as it is long.
a. Draw a diagram of the poster, and label its dimensions.
Answer:
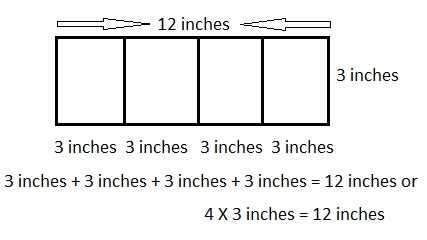
Explanation:
Labeled the diagram of the poster with the dimensions as shown above, long = 3 inches, and wide is 4 × 3 inches = 12 inches.
b. Find the perimeter and area of the poster.
Answer:
Perimeter of the poster is 30 inches and area of the poster is 36 square inches,
Explanation:
Given poster as 3 inches long and 4 X 3 inches = 12 inches wide,
So perimeter of the poster is 2 X ( 3 inches + 12 inches) =
2 × 15 inches = 30 inches and area of the poster is 3 inches × 12 inches = 36 square inches.
Question 3.
The area of a rectangle is 36 square centimeters, and its length is 9 centimeters.
a. What is the width of the rectangle?
Answer:
The width of the rectangle is 4 centimeters,
Explanation:
Given the area of a rectangle is 36 square centimeters
and its length is 9 centimeters so width of the rectangle is 36 sq cm = 9 cm X width , width = 36 cm X cm ÷ 9 cm = 4 cm,
therefore the width of the rectangle is 4 centimeters.
b. Elsa wants to draw a second rectangle that is the
same length but is 3 times as wide. Draw and label
Elsa’s second rectangle.
Answer:
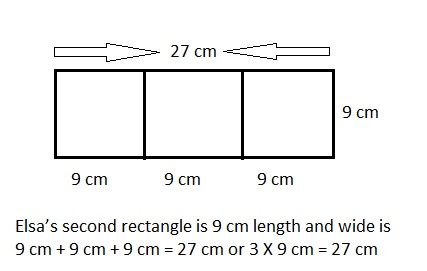
Explanation:
Given Elsa wants to draw a second rectangle that is the same length but is 3 times as wide. Drawn and labeled
Elsa’s second rectangle with length as 9 centimeters and wide as 3 X 9 cm = 27 centimeters.
c. What is the perimeter of Elsa’s second rectangle?
Answer:
Perimeter of Elsa’s second rectangle is 72 centimeters,
Explanation:
Given Elsa’s second rectangle is with length 9 cm and wide is 27 cm, So perimeter is 2 X (9 cm + 27 cm) =
2 × (36 cm) = 72 centimeters.
therefore, Perimeter of Elsa’s second rectangle is 72 centimeters.
Question 4.
The area of Nathan’s bedroom rug is 15 square feet. The longer side measures 5 feet. His living room rug is twice as long and twice as wide as the bedroom rug.
a. Draw and label a diagram of Nathan’s bedroom rug. What is its perimeter?
Answer:

Perimeter of Nathan’s bedroom rug is 16 feet,
Explanation:
Given the area of Nathan’s bedroom rug is 15 square feet.
The longer side measures 5 feet so width is 15 feet × feet ÷ 5 feet = 3 feet, now preimeter of
Nathan’s bedroom rug is 2 X (5 feet + 3 feet) =
2 × 8 feet = 16 feet, Drawn and labeled a diagram of Nathan’s bedroom rug as shown above.
b. Draw and label a diagram of Nathan’s living room rug. What is its perimeter?
Answer:
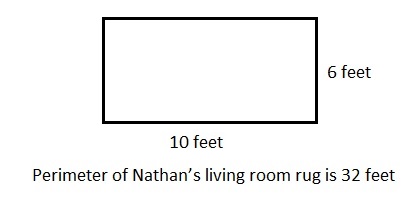
Perimeter of Nathan’s living room rug is 32 feet,
Explanation:
Drawn and labeled a diagram of Nathan’s living room rug as shown above with long as 2 × 5 feet = 10 feet and
width as 2 × 3 feet = 6 feet.
Perimeter of Nathan’s living room rug is 2 × (10 feet + 6 feet) = 2 × 16 feet = 32 feet.
c. What is the relationship between the two perimeters?
Answer:
The perimeter of Nathan’s living room rug is twice the perimeter of Nathan’s bedroom rug,
Explanation:
As perimeter of Nathan’s bedroom rug is 16 feet and perimeter of Nathan’s living room rug is 32 feet and as both length and width of Nathan’s living room rug is twice of Nathan’s bedroom rug.
d. Find the area of the living room rug using the formula A = l × w.
Answer:
The area of the living room rug is 60 square feet,
Explanation:
Given living room rug has long 10 feet and width 6 feet,
So area of the living room rug is 10 feet X 6 feet = 60 square feet.
e. The living room rug has an area that is how many
times that of the bedroom rug?
Answer:
The living room rug has an area that is four times that of the bedroom rug,
Explanation:
The area of the living room rug is 60 square feet and
the area of Nathan’s bedroom rug is 15 square feet.
So number of times the area of the living room rug to
the area of Nathan’s bedroom rug is 60 sq feet ÷ 15 square feet = 4,
Therefore, the living room rug has an area that is four times that of the bedroom rug.
f. Compare how the perimeter changed with how the area changed between the two rugs. Explain what you notice using words, pictures, or numbers.
Answer:
Nathan’s living room has twice perimeter and area has became four times that of Nathan’s bedroom rug,
Explanation:
As we know Perimeter of is Nathan’s bedroom rug 16 feet and perimeter of Nathan’s living room is 32 feet,
Area of Nathan’s bedroom rug is 15 square feet and area of Nathan’s living room is 60 square feet, Now on comparing Nathan’s living room has twice perimeter and area has became four times to that of Nathan’s bedroom rug.