Teachers and students can find this Eureka Answer Key for Grade 3 more helpful in raising students’ scores and supporting teachers to educate the students. Eureka Math Answer Key for Grade 3 aids teachers to differentiate instruction, building and reinforcing foundational mathematics skills that alter from the classroom to real life. With the help of Eureka’s primary school Grade 3 Answer Key, you can think deeply regarding what you are learning, and you will really learn math easily just like that.
Engage NY Eureka Math 3rd Grade Module 3 Lesson 3 Answer Key
Teachers and students can find this Eureka Answer Key for Grade 3 more helpful in raising students’ scores and supporting teachers to educate the students. Eureka Math Answer Key for Grade 3 aids teachers to differentiate instruction, building and reinforcing foundational mathematics skills that alter from the classroom to real life. With the help of Eureka’s primary school Grade 3 Answer Key, you can think deeply regarding what you are learning, and you will really learn math easily just like that.
Eureka Math Grade 3 Module 3 Lesson 3 Problem Set Answer Key
Question 1.
Each equation contains a letter representing the unknown. Find the value of the unknowns, and then write the letters that match the answers to solve the riddle.
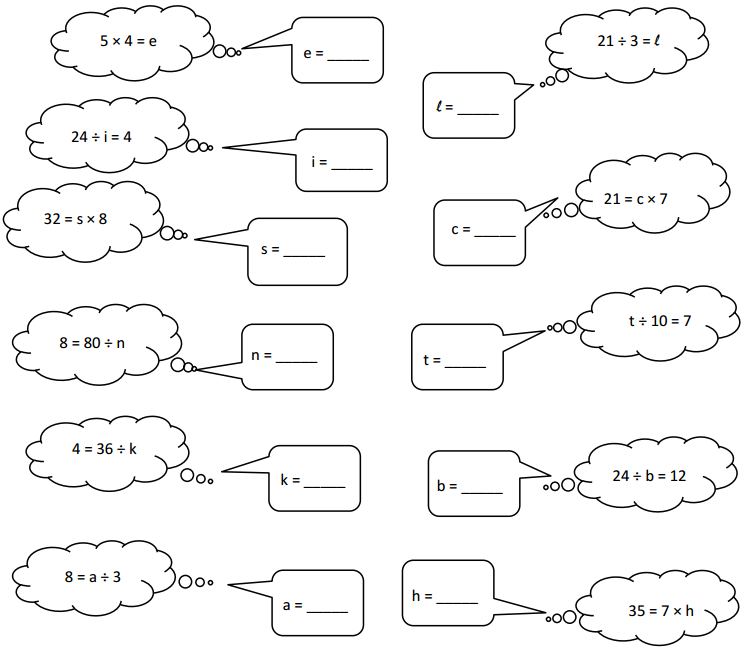
Answer:
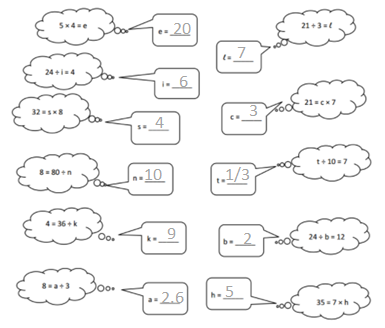
e = 20, i = 1/ 6, s = 4, n = 10, k = 6, a = 2.6, l = 7, c = 3, t = 0.7, b = 2, h = 5.
Explanation:
In the above-given question,
given that,
The equation contains the letter representing unknown.
5 x 4 = e , e = 20.
24/ i = 4, i = 4/ 24 = 1/6.
32 = s x 8, s = 32/ 8, s = 4.
8 = 80 / n, n = 10.
8 = a / 3, a = 2.6.
21 / 3 = l, l = 7.
21 = c x 7, c = 3.
t / 10 = 7, t = 0.7.
24/b = 12, b = 24/ 12, b = 2.
35 = 7 x h, h = 5.
Which tables do you NOT have to learn?
![]()
Answer:
The tables not have to learn is 10, 20, and 70.
Explanation:
In the above-given question,
given that,
The tables are 9, 6, 3, 5, 70, 20, 10, 24, 2, 7, and 4.
out of all the tables 10 and 20 are very easy.
so we need not to learn.
Question 2.
Lonna buys 3 t-shirts for $8 each.
a. What is the total amount Lonna spends on 3 t-shirts? Use the letter m to represent the total amount of money Lonna spends, and then solve the problem.
Answer:
The total amount of money Lonna spends = 24$.
Explanation:
In the above-given question,
given that,
Lonna buys 3 t-shirts for $8 each.
m x 3 = $8.
m = 8 x 3.
m = $24.
so the total amount of money Lonna spends = $24.
b. If Lonna hands the cashier 3 ten dollar bills, how much change will she receive? Use the letter c in an equation to represent the change, and then find the value of c.
Answer:
The change she received = $6.
Explanation:
In the above-given question,
given that,
Lonna hands the cashier 3 ten dollar bills.
c x 30 = 24.
c = 30 – 24.
c = $6.
so the change Lonna received = $6.
Question 3.
Miss Potts used a total of 28 cups of flour to bake some bread. She used 4 cups of flour for each loaf of bread. How many loaves of bread did she bake? Represent the problem using multiplication and division sentences and a letter for the unknown. Then, solve the problem.
__7___ × ___4__ = __28____
__28___ ÷ __4___ = ___7___
Answer:
The number of loaves of bread did she bake = 7.
Explanation:
In the above-given question,
given that,
Miss potts used a total of 28 cups of flour to bake some bread.
she used 4 cups of flour for each loaf of bread.
7 x 4 = 28.
28 / 4 = 7.
so the number of loaves of bread did she bake = 7.
Question 4.
At a table tennis tournament, two games went on for a total of 32 minutes. One game took 12 minutes longer than the other. How long did it take to complete each game? Use letters to represent the unknowns. Solve the problem.

Answer:
The other game takes to complete = 10 minutes.
Explanation:
In the above-given question,
given that,
At a table tennis tournament, two games went on for a total of 32 minutes.
one game took 12 minutes longer than the other.
32 + t = 12.
t = 32 – 12.
t = 20.
so the other game takes to complete = 10 minutes.
Eureka Math Grade 3 Module 3 Lesson 3 Exit Ticket Answer Key
Find the value of the unknown in Problems 1 – 4.
Question 1.
z = 5 × 9
z = ___45___
Answer:
z = 45.
Explanation:
In the above-given question,
given that,
the equation z = 5 x 9.
z = 45.
Question 2.
30 ÷ 6 = v
v = ___5___
Answer:
v = 5.
Explanation:
In the above-given question,
given that,
the equation 30/ 6 = v.
v = 5.
Question 3.
8 × w = 24
w = ____3__
Answer:
w = 3.
Explanation:
In the above-given question,
given that,
the equation 8 x w = 24.
w = 24/8.
w = 3.
Question 4.
y ÷ 4 = 7
y = __1.75____
Answer:
y = 1.75.
Explanation:
In the above-given question,
given that,
y / 4 = 7.
y = 7 / 4.
y = 1.75.
Question 5.
Mr. Strand waters his rose bushes for a total of 15 minutes. He waters each rose bush for 3 minutes. How many rose bushes does Mr. Strand water? Represent the problem using multiplication and division sentences and a letter for the unknown. Then, solve the problem.
__3___ × __5___ = __15___
__15___ ÷ __3___ = ___5__
Answer:
The number of rose bushes Mr. strand water = 15.
Explanation:
In the above-given question,
given that,
Mr. Strand waters his rose bushes for a total of 15 minutes.
He waters each rose bush for 3 minutes.
3 x 5 = 15.
15 / 3 = 5.
so the number of rose bushes Mr. Strand water = 15.
Eureka Math Grade 3 Module 3 Lesson 3 Homework Answer Key
Question 1.
a. Complete the pattern.

Answer:
The missing numbers in the pattern are 40, 50, 70, 80, and 100.
Explanation:
In the above-given question,
given that,
the pattern with numbers.
the missing numbers are 40, 50, 70, 80, and 100.

b. Find the value of the unknown.
10 × 2 = d d = __20___
3 × 10 = e e = __30___
f = 4 × 10 f = ___40__
p = 5 × 10 p = __50___
10 × 6 = w w = ___60__
10 × 7 = n n = __70___
g = 8 × 10 g = __80___
Answer:
d = 20.
e = 30.
f = 40.
p = 50.
w = 60.
n = 70.
g = 80.
Explanation:
In the above-given question,
given that,
the equations 10 x 2 = d, d = 20.
3 x 10 = e, e = 30.
f = 4 x 10, f = 40.
p = 5 x 10, p = 50.
10 x 6 = w, w = 60.
10 x 7 = n, n = 70.
g = 8 x 10, g = 80.
Question 2.
Each equation contains a letter representing the unknown. Find the value of the unknown.
| 8 ÷ 2 = n | n = _4____ |
| 3 × a = 12 | a = __4___ |
| p × 8 = 40 | p = __5___ |
| 18 ÷ 6 = c | c = __3___ |
| d × 4= 24 | d = ___6__ |
| h ÷ 7 = 5 | h = __1.4___ |
| 6 × 3 = f | f = ___18__ |
| 32 ÷ y = 4 | y = __8___ |
Answer:
n = 4.
a = 4.
p = 5.
c = 3.
d = 6.
h = 1.4.
f = 18.
y = 8.
Explanation:
In the above-given question,
given that,
the equations 8 / 2 = n, n = 4.
3 x a = 12, a = 12 / 3, a = 4.
p x 8 = 40, p = 40 / 8, p = 5.
18 / 6 = c, c = 3.
d x 4 = 24, d = 24 / 4, d = 6.
h / 7 = 5, h = 1.4.
6 x 3 = f, f = 18.
32 / y = 4. y = 8.
Question 3.
Pedro buys 4 books at the fair for $7 each.
a. What is the total amount Pedro spends on 4 books? Use the letter b to represent the total amount Pedro spends, and then solve the problem.
Answer:
The total amount Pedro spends on 4 books = $28.
Explanation:
In the above-given question,
given that,
Pedro buys 4 books at the fair for $7 each.
b x 4 = 7.
b = 7 x 4.
b = $28.
so the total amount Pedro spends on 4 books = $28.
b. Pedro hands the cashier 3 ten dollar bills. How much change will he receive? Write an equation to solve. Use the letter c to represent the unknown.
Answer:
The change Pedro receives = $2.
Explanation:
In the above-given question,
given that,
Pedro hands the cashier 3 ten dollar bills.
c + 30 = 28.
c = 30 – 28.
c = $2.
Question 4.
On field day, the first-grade dash is 25 meters long. The third-grade dash is twice the distance of the first-grade dash. How long is the third-grade dash? Use a letter to represent the unknown and solve.
Answer:
The third-grade dash = 75 meters long.
Explanation:
In the above-given question,
given that,
On field day, the first-grade dash is 25 meters long.
The third-grade dash is twice the distance of the first-grade dash.
g = 25 + 50.
g = 75.
so the third-grade dash = 75 meters long.