Go through the enVision Math Common Core Grade 4 Answer Key Topic 13 Measurement: Find Equivalence in Units of Measure and finish your homework or assignments.
enVision Math Common Core 4th Grade Answers Key Topic 13 Measurement: Find Equivalence in Units of Measure
Essential Questions:
How can you convert from one unit to another? How can you be precise when solving math problems?

enVision STEM Project: Erosion and Measurement
Do Research The Colorado River has played a large part in shaping North America. Use the Internet and other resources to research the states through which the river travels.
Journal: Write a Report Include what you found. Also in your report:
- Look up geology and geometry in the dictionary. Write the definitions and explain how these words are related. What does the prefix “geo” mean in both words?
- A.J. takes a 4-mile tour of the Grand Canyon. Explain how to convert the length of A.J.’s tour from miles to feet.
Review What You Know
Vocabulary
Choose the best term from the box. Write it on the blank.
- capacity
- gram
- liter
- mass
Question 1.
The amount of liquid a container can hold is called its ________.
Answer:
The amount of liquid a container can hold is called its __capacity______.
Question 2.
________ is the amount of matter that something contains.
Answer:
___Mass_____ is the amount of matter that something contains.
Question 3.
One metric unit of capacity is a ________.
Answer:
One metric unit of capacity is a __Liter______.
Perimeter
Find the perimeter of each shape.
Question 4.

Answer:
Perimeter of the given rectangle shape = 134 centimeters.
Explanation:
Length of the given rectangle shape = 42 centimeters.
Width of the given rectangle shape = 25 centimeters.
Perimeter of the given rectangle shape = 2 × (Length of the given rectangle shape × Width of the given rectangle shape)
= 2 × (42 + 25)
= 2 × 67
= 134 centimeters.
Question 5.

Answer:
Perimeter of the given square shape = 28 feet.
Explanation:
Length of the given square shape = 7 feet.
Perimeter of the given square shape = 4 × Length of the given square shape
= 4 × 7
= 28 feet.
Question 6.

Answer:
Perimeter of the given Triangular shape = 9 yards.
Explanation:
Length of the given Triangular shape = 3 yards.
Perimeter of the given Triangular shape = Length of the given Triangular shape + Length of the given Triangular shape + Length of the given Triangular shape
= 3 + 3 + 3
= 9 yards.
Question 7.
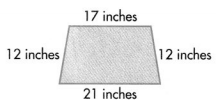
Answer:
Perimeter of the given Quadrilateral shape = 62 inches.
Explanation:
Length of the given Quadrilateral shape:
Side 1 length = 17 inches.
Side 2 length = 12 inches.
Side 3 length = 21 inches.
Side 4 length = 12 inches.
Perimeter of the given Quadrilateral shape = Side 1 length + Side 2 length + Side 3 length + Side 4 length
= 17 + 12 + 21 + 12
= 29 + 21 + 12
= 50 + 12
= 62 inches.
Question 8.
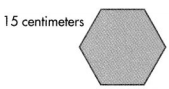
Answer:
Perimeter of the given hexagon shape = 90 centimeters.
Explanation:
Length of the given hexagon shape = 15 centimeters.
Perimeter of the given hexagon shape = 6 × Length of the given hexagon shape
= 6 × 15
= 90 centimeters.
Question 9.
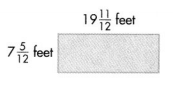
Answer:
Perimeter of the given rectangle shape = 40.67 feet.
Explanation:
Length of the given rectangle shape = 19 (11/12) feet.
Width of the given rectangle shape = 7 (5/12) feet.
Perimeter of the given rectangle shape = 2 × (Length of the given rectangle shape × Width of the given rectangle shape)
= 2 × (19 11/12 + 7 5/12)
= 2 × (209/12 + 35/12)
= 2 × 244/12
= 488/12
= 40.67 feet.
Area
Find the area of each shape.
Question 10.
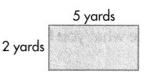
Answer:
Area of the given rectangle shape = 10 square yards.
Explanation:
Length of the given rectangle shape = 5 yards.
Width of the given rectangle shape = 2 yards.
Area of the given rectangle shape = Length of the given rectangle shape × Width of the given rectangle shape
= 5 × 2
= 10 square yards.
Question 11.
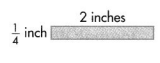
Answer:
Area of the given rectangle shape = 1/2 or 0.5 inches.
Explanation:
Length of the given rectangle shape = 2 inches.
Width of the given rectangle shape = 1/4 inches.
Area of the given rectangle shape = Length of the given rectangle shape × Width of the given rectangle shape
= 2 × 1/4
= 1/2 or 0.5 inches.
Question 12.
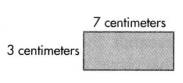
Answer:
Area of the given rectangle shape = 21 square centimeters.
Explanation:
Length of the given rectangle shape = 7 centimeters.
Width of the given rectangle shape = 3 centimeters.
Area of the given rectangle shape = Length of the given rectangle shape × Width of the given rectangle shape
= 7 × 3
= 21 square centimeters.
Problem Solving
Question 13.
Make Sense and Persevere A league is a nautical measurement equal to about 3 miles. If a ship travels 2,000 leagues, about how many miles does the ship travel?
Answer:
Number of miles the ship travelled = 6000 miles.
Explanation:
1 league = 3 miles.
Number of leagues the ship travelled = 2000.
Number of miles the ship travelled = 3 × Number of leagues the ship travelled
=> 3 × 2000
=> 6000 miles.
Pick a Project
PROJECT 13A
What makes the St. Johns River special?
Project: Make a Travel Brochure About Rivers in Your Home State

Answer:

PROJECT 13B
How are tin cans useful?
Project: Cooking on a Budget

Answer:
Ways to Cook on a Budget
- Make meal plans.
- Shop for groceries at a discount grocer.
- Start with the grocery store flyer.
- Pair sale items with low-cost staple foods.
- Use a slow cooker.
- Make “pantry meals” a habit.
- Make extras and freeze them.
- Eat your leftovers.
PROJECT 13C
Who invented the jigsaw puzzle?
Project: Make Your Own Jigsaw Puzzle

Answer:

3-ACT MATH PREVIEW
Math Modeling
A Pint’s a Pound

I can … model with math to solve a problem that involves estimating and computing with units of weight and capacity.
Lesson 13.1 Equivalence with Customary Units of Length
Solve & Share
Jeremy jogged 75 yards from his house to school. How many feet did Jeremy jog? Solve this problem any way you choose.
I can … convert customary units of length from one unit to another and recognize the relative size of different units.

Look Back! Look for Relationships What do you notice about the relationship between the number of yards and the number of feet Jeremy jogged?
Answer:
The relationship between the number of yards and the number of feet Jeremy jogged is 3 times more than the number of yards Jeremy jogged.
Explanation:
Number of yards Jeremy jogged = 75.
Number of feet Jeremy jog = 3 × Number of yards Jeremy jogged
= 3 × 75
= 225 feet.
Essential Question
How Can You Convert from One Unit of Length to Another?
Answer:
We can Convert from One Unit of Length to Another, by following steps:
1. Write the conversion as a fraction (that equals one)
2. Multiply it out (leaving all units in the answer)
3. Cancel any units that are both top and bottom.
Visual Learning Bridge
Maggie has a tree swing. How many inches long is each rope from the bottom of the branch to the swing?
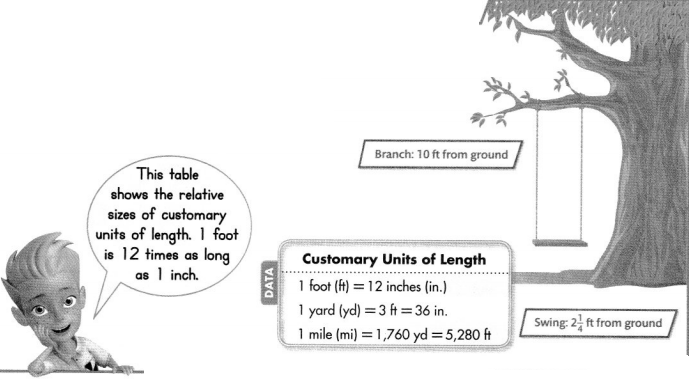
Step 1
Find the length of the rope in feet. r = 10 – 2\(\frac{1}{4}\)

Each rope is 7\(\frac{3}{4}\) feet long.
Step 2
Convert the length of the rope to inches.

Each rope is 93 inches long.
Convince Me! Generalize How do you know the answer is reasonable when converting a larger unit to a smaller unit?
Answer:
When converting a larger unit to a smaller one, you multiply; when you convert a smaller unit to a larger one, you divide. Hence, the answer is reasonable when converting a larger unit to a smaller unit.
Another Example!
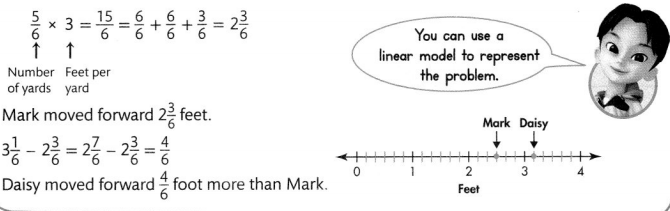
Mark moved forward yard when doing a back flip. Daisy moved forward 3\(\frac{1}{6}\) feet. How much more did Daisy move forward than Mark? One yard is 3 times as long as a foot.
Guided Practice
Do You Understand?
Question 1.
Does it take more inches or feet to equal a given length? Explain.
Answer:
Converting Between Units of Length:
There are many more inches for a measurement than there are feet for the same measurement, as feet is a longer unit of measurement. You could use the conversion factor.
Question 2.
Which is a greater distance, 9 yards or 9 miles?
Answer:
9 miles is a greater distance between 9 yards or 9 miles.
Explanation:
1 miles = 1760 yards.
9 miles = ??? yards.
=> 9 × 1760
=> 15840 yards.
Do You Know How?
For 3-4, convert each unit.
Question 3.
2 miles = _________ yards
Answer:
2 miles = __3520 _______ yards.
Explanation:
1 miles = 1760 yards.
2 miles = 2 × 1760
=> 3520 yards.
Question 4.
\(\frac{2}{3}\) yard = _____feet
Answer:
\(\frac{2}{3}\) yard = __2___feet.
Explanation:
1 yard = 3 feet.
\(\frac{2}{3}\) yard = \(\frac{2}{3}\) × 3
=> 2 feet.
Independent Practice
In 5-7, write > or < in each ![]() to compare the measures.
to compare the measures.
Question 5.
6 inches ![]() 6 feet
6 feet
Answer:
6 inches < 6 feet.
Explanation:
1 feet = 12 inches.
6 feet = 6 × 12
=> 72 inches.
Question 6.
2 yards ![]() 7 feet
7 feet
Answer:
2 yards < 7 feet.
Explanation:
1 yard = 3 feet.
2 yards = 2 × 3
=> 6 feet.
Question 7.
4 yards ![]() 100 inches
100 inches
Answer:
4 yards > 100 inches.
Explanation:
1 yard = 36 inches.
4 yards = 4 × 36
=> 144 inches.
For 8-11, convert each unit.
Question 8.
8 yards = _______ inches
Answer:
8 yards = __288_____ inches.
Explanation:
1 yard = 36 inches.
8 yards = 8 × 36
=> 288 inches.
Question 9.
28 yards = ______ feet
Answer:
28 yards = __84____ feet.
Explanation:
1 yard = 3 feet.
28 yards = 3 × 28
=> 84 feet.
Question 10.
18 feet = ________ inches
Answer:
18 feet = ___216_____ inches.
Explanation:
1 feet = 12 inches.
18 feet = 12 × 18
=> 216 inches.
Question 11.
7 miles = ______ yards
Answer:
7 miles = __12320____ yards.
Explanation:
1 mile = 1760 yards.
7 miles = 1760 × 7
=> 12320 yards.
Problem Solving
Question 12.
Be Precise Lou cuts 3 yards from a 9-yard roll of fabric. Then he cuts 4 feet from the roll. How many feet of fabric are left on the roll?
Answer:
Remaining feet of fabric are left on the roll = 14.
Explanation:
Length of fabric Lou cuts = 3 yards.
Length of roll of fabric = 9 yards.
Remaining length of roll of fabric = Length of roll of fabric – Length of fabric Lou cuts
= 9 – 3
= 6 yards.
Conversion: 1 yard = 3 feet.
= 6 yards = ??? feet
=> 6 × 3 feet
= 18 feet.
Length of fabric later cut = 4 feet.
Remaining feet of fabric are left on the roll = Remaining length of roll of fabric – Length of fabric later cut
= 18 – 4
= 14 .
Question 13.
What customary units would you use to measure the length of a praying mantis? Explain.
Answer:
The customary system of measurement is inches used to measure the length of a praying mantis.
Explanation:
The customary system of measurement is defined as a set of weights and measures used for measuring length, weight, capacity, and temperature. Most praying mantis are no more than 5 inches in length. The smaller species measure around 2 to 3 inches while the bigger specimens reach the overall length of 6 to 7 inches.
Question 14.
Algebra On the field trip, Toni collected 4 times as many bugs as Kaylie. Kaylie collected 14 bugs. Draw a bar diagram, and write and solve an equation to find b, how many bugs Toni collected.
Answer:
Number of bugs Toni collected = 56.
Explanation:
Number of bugs Kaylie collected = 14.
Toni collected 4 times as many bugs as Kaylie.
Number of bugs Toni collected = 4 × Number of bugs Kaylie collected
= 4 × 14
=> 56.
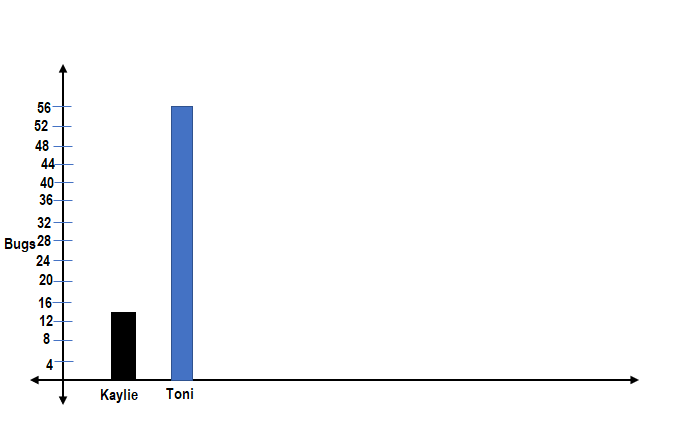
Question 15.
Which is greater, 3 miles or 5,000 yards? How much greater? Explain.
Answer:
3 miles is greater by 280 yards than 5,000 yards.
Explanation:
3 miles,5000 yards.
Conversion: 1 mile = 1760 yards.
3 miles = ??? yards
=> 3 × 1760
=> 5280 yards.
Difference:
5280 yards – 5000 yards
=> 280 yards.
Question 16.
Higher Order Thinking Jenna uses \(\frac{1}{2}\) yard of ribbon for each box she wraps. How many inches of ribbon does she need to wrap 4 boxes? Use the linear model to help solve.
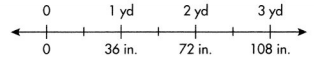
Answer:
Number of inches of ribbon she needs to wrap 4 boxes = 72 inches.
Explanation:
Length of ribbon Jenna uses for each box she wraps = \(\frac{1}{2}\) yard.
Total Length of ribbon she needs to wrap 4 boxes = 4 × Length of ribbon Jenna uses for each box she wraps
= 4 × \(\frac{1}{2}\) yard
= 2 yards.
Conversion: 1 yard = 36 inches.
Number of inches of ribbon she needs to wrap 4 boxes = Total Length of ribbon she needs to wrap 4 boxes × 36 inches
= 2 × 36
=> 72 inches.

Assessment Practice
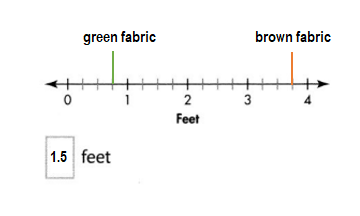
Question 17.
Connor has 3\(\frac{3}{4}\) feet of brown fabric and \(\frac{3}{4}\) yard of green to make a costume for the school play. How many more feet of brown than green fabric does Connor have? Show both measures with points on the number line.
Answer:
1 \(\frac{2}{4}\) feet more feet of brown than green fabric Connor have.
Explanation:
Length of brown fabric Connor has = 3\(\frac{3}{4}\) feet.
Length of green fabric Connor has = \(\frac{3}{4}\) yard
Conversion: 1 yard = 3 feet.
\(\frac{3}{4}\) yard = ?? feet
=> 3 × \(\frac{3}{4}\)
=> 2 \(\frac{1}{4}\) feet.
Difference:
Length of brown fabric Connor has – Length of green fabric Connor has
= 3\(\frac{3}{4}\) feet – 2 \(\frac{1}{4}\) feet
= 1 \(\frac{2}{4}\) feet.
Question 18.
Charlotte made \(\frac{11}{2}\) yard of a paper chain for the school dance. Josh made 4\(\frac{1}{12}\) feet, and Mika made 3\(\frac{4}{12}\) feet. How many feet of chain did they make in all?
A. 8\(\frac{4}{12}\) feet
B. 9\(\frac{4}{12}\) feet
C. 10\(\frac{2}{12}\) feet
D. 10\(\frac{4}{12}\) feet
Answer:
Total length of feet of chain they make in all = 9\(\frac{4}{12}\) feet.
B. 9\(\frac{4}{12}\) feet.
Explanation:
Length of a paper chain Charlotte made = \(\frac{11}{2}\) yard.
Conversion:
1 yard = 3 feet.
\(\frac{11}{2}\) yard = \(\frac{11}{2}\) × 3
= 16 \(\frac{1}{2}\) feet.
Length of a paper chain Josh made = 4\(\frac{1}{12}\) feet.
Length of a paper chain Mika made = 3\(\frac{4}{12}\) feet.
Total length of feet of chain they make in all = Length of a paper chain Charlotte made + Length of a paper chain Josh made + Length of a paper chain Mika made
= 16 \(\frac{1}{2}\) feet + 4\(\frac{1}{12}\) feet + 3\(\frac{4}{12}\) feet
= 9\(\frac{4}{12}\) feet.
Lesson 13.2 Equivalence with Customary Units of Capacity
Solve & Share
Casey has \(\frac{1}{2}\) gallon of juice. How many 1-pint containers can he fill? Solve this problem any way you choose.
I can … convert customary units of capacity from one unit to another and recognize the relative size of different units.

Look Back! Generalize How did you convert from a larger unit of capacity to a smaller unit of capacity? Did you use the same process you used to convert from a larger unit of length to a smaller unit of length? Explain.
Answer:
When converting a larger unit of capacity to a smaller one of capacity, you multiply; when you convert a smaller unit of capacity to a larger one of capacity, you divide.
Yes, I used the same process you used to convert from a larger unit of length to a smaller unit of length.
Essential Question
How Can You Convert from One Unit of Capacity to Another?
Answer:
We can convert from One Unit of Capacity to Another by converting a larger unit of capacity to a smaller one of capacity, you multiply; when you convert a smaller unit of capacity to a larger one of capacity, you divide.
Visual Learning Bridge
Ms. Nealy’s class needs 5 gallons of punch for family math night. How much of each ingredient is needed to make enough punch with the recipe shown?
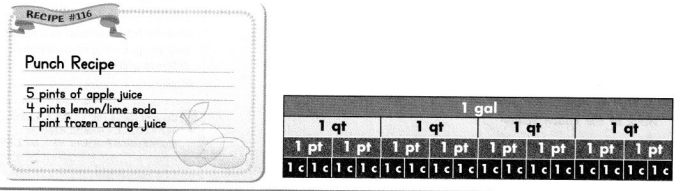
Units of capacity include gallons, quarts, pints, cups, and fluid Ounces.
Capacity is how much liquid a container can hold. This diagram shows the relative sizes of customary units of capacity. 1 gallon is 4 times as much as 1 quart
Step 1
Convert 5 gallons to pints.

5 gallons = 40 pints
Step 2
Add the number of pints in the recipe to find how many batches the class needs to make.
5 + 4 +1 = 10
10 × n = 40
n = 4
The class needs to make 4 batches of the recipe.
Step 3
Find how much of each ingredient is in 4 batches.
4 × 5 = 20 pints
4 × 4 = 16 pints
4 × 1 = 4 pints
20 pints of apple juice, 16 pints of lemon/lime soda, and 4 pints of frozen orange juice are needed.
Convince Me! Reasoning Complete the sentence below.
One gallon equals _______ quarts, _______ pints, or _______ cups.
Answer:
One gallon equals ___4____ quarts, ____8___ pints, or ___16____ cups.
Explanation:
1 gallon = 8 pints.
1 gallon = 4 quarts.
1 gallon = 16 cups.
Guided Practice
Do You Understand?
Question 1.
How many cups of punch does 5 gallons of the punch from the previous page make?
Answer:
Number of cups of punch 5 gallons of the punch from the previous page makes = 80 cups.
Explanation:

Number of cups of punch 5 gallons of the punch from the previous page makes =
5 gallons = ??? cups
Conversion:
1 gallon = 16 cups.
5 gallons = 5 × 16
= 80 cups.
Question 2.
Which size container holds more, 3 pints or 3 quarts?
Answer:
3 quarts size container holds more.
Explanation:
3 pints and 3 quarts.
1 quarts = 2 pints.
3 quarts = 3 × 2
= 6 pints.
Do You Know How?
For 3-5, convert each unit.
Question 3.
2 cups = _______ fluid ounces
Answer:
2 cups = ___16____ fluid ounces.
Explanation:
Conversion: 1 cup = 8 fluid ounces.
2 cups = 8 × 2
= 16 fluid ounces.
Question 4.
\(\frac{1}{2}\) gallon = _______ pints
Answer:
\(\frac{1}{2}\) gallon = ___4____ pints.
Explanation:
Conversion: 1 gallon = 8 pints.
\(\frac{1}{2}\) gallon = 8 × \(\frac{1}{2}\)
= 4 pints.
Question 5.
5 pints = ______ cups
Answer:
5 pints = __10____ cups.
Explanation:
Conversion: 1 pint = 2 cups.
5 pints = 2 × 5
= 10 cups.
Independent Practice
In 6-8, write > or < in each ![]() to compare the measures.
to compare the measures.
Question 16.
2 pints ![]() 2 gallons
2 gallons
Answer:
2 pints < 2 gallons.
Explanation:
2 pints and 2 gallons.
Conversion: 1 gallon = 8 pints.
2 gallons = 8 × 2
= 16 pints.
Question 7.
5 quarts ![]() 8 pints
8 pints
Answer:
5 quarts > 8 pints.
Explanation:
5 quarts and 8 pints.
Conversion: 1 quart = 2 pints.
5 quarts = 2 × 5
= 10 pints.
Question 8.
10 cups ![]() 2 quarts
2 quarts
Answer:
10 cups > 2 quarts.
Explanation:
10 cups and 2 quarts.
Conversion: 1 quart = 4 cups.
2 quarts = 4 × 2
= 8 cups.
For 9-12, convert each unit.
Question 9.
7 quarts = ________ cups
Answer:
7 quarts = ____28____ cups.
Explanation:
Conversion: 1 quart = 4 cups.
7 quarts = 4 × 7
= 28 cups.
Question 10.
12 gallons = ______ quarts
Answer:
12 gallons = ___48___ quarts.
Explanation:
Conversion: 1 gallon = 4 quarts.
12 gallons = 4 × 12
= 48 quarts.
Question 11.
7 pints = _______ fluid ounces
Answer:
7 pints = __112_____ fluid ounces.
Explanation:
Conversion: 1 pint = 16 fluid ounces.
7 pints = 16 × 7
= 112 fluid ounces.
Question 12.
\(\frac{3}{4}\) gallon = ______ pints
Answer:
\(\frac{3}{4}\) gallon = ___6___ pints.
Explanation:
Conversion: 1 gallon = 8 pints.
\(\frac{3}{4}\) gallon = 8 × \(\frac{3}{4}\)
= 6 pints.
For 13-14, convert each unit.
Question 13.
Answer:
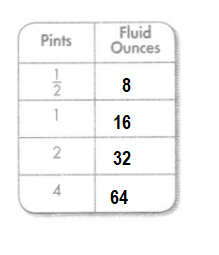
Explanation:
Conversion: 1 pint = 16 fluid ounces.
\(\frac{2}{4}\) = 16 × \(\frac{2}{4}\)
= 8 fluid ounces.
1 pint = 16 fluid ounces.
2 pints = 16 × 2
= 32 fluid ounces.
4 pints = 16 × 4
= 64 fluid ounces.
Question 14.

Answer:

Explanation:
Conversion: 1 gallon = 16 cups.
2 gallon = 16 × 2 = 32 cups.
3 gallon = 16 × 3 = 48 cups.
4 gallon = 16 × 4 = 64 cups.
Problem Solving
Question 15.
en Vision® STEM Scientists measure how much water and debris flow past a river station at different times of the year. The water and debris are called discharge. The table shows the average discharge at the Camp Verde station on the Verde River in two months. How many more quarts of discharge per second are there in December than November?

Answer:
2664 more quarts of discharge per second are there in December than November .
Explanation:
Average discharge at the Camp Verde station on the Verde River for November month = 1619 gallons per second.
Average discharge at the Camp Verde station on the Verde River for December month = 2285 gallons per second.
Conversion: 1 gallon = 4 quarts.
Number of quarts of discharge per second in November = Average discharge at the Camp Verde station on the Verde River for November month × 4
= 1619 × 4
= 6476 quarts.
Number of quarts of discharge per second in December = Average discharge at the Camp Verde station on the Verde River for December month × 4
= 2285 × 4
= 9140 quarts.
Difference:
Number of quarts of discharge per second in December – Number of quarts of discharge per second in November
= 9140 – 6476
= 2664 .
Question 16.
How many quarts of discharge per second were recorded in November and December?
Answer:
Number of quarts of discharge per second in November = 6476 quarts.
Number of quarts of discharge per second in December = 9140 quarts.
Explanation:
Conversion: 1 gallon = 4 quarts.
Number of quarts of discharge per second in November = Average discharge at the Camp Verde station on the Verde River for November month × 4
= 1619 × 4
= 6476 quarts.
Number of quarts of discharge per second in December = Average discharge at the Camp Verde station on the Verde River for December month × 4
= 2285 × 4
= 9140 quarts.
Question 17.
Make Sense and Persevere Annabelle had the following containers of paint left over: \(\frac{1}{2}\) gallon, \(\frac{3}{4}\) quart, and \(\frac{1}{4}\) gallon. How many quarts of paint does Annabelle have left over? Explain.
Answer:
Total quarts of paint does Annabelle have left over = 3 \(\frac{3}{4}\) quarts.
Explanation:
Quantity of containers of paint left over:
First container = \(\frac{1}{2}\) gallon.
Second container = \(\frac{3}{4}\) quart.
Third container = \(\frac{1}{4}\) gallon.
Conversion: 1 gallon = 4 quarts.
First container = \(\frac{1}{2}\) gallon.
= \(\frac{1}{2}\) × 4
= 2 quarts.
Third container = \(\frac{1}{4}\) gallon.
= \(\frac{1}{4}\) × 4
= 1 quarts.
Total quarts of paint does Annabelle have left over = First container + Second container + Third container
= 2 quarts + \(\frac{3}{4}\) + 1 quarts
= 3 \(\frac{3}{4}\) quarts.
Question 18.
Higher Order Thinking A caterer combines 3 quarts of orange juice, 5 pints of milk, and 5 cups of pineapple juice to make smoothies. How many cups can be filled with smoothies? Explain.
Answer:
Number of cups can be filled with smoothies = 27 cups.
Explanation:
Quantity of orange juice = 3 quarts.
Quantity of pints of milk = 5 pints.
Quantity of cups of pineapple juice = 5 cups.
Conversion: 1 pint = 2 cups.
Quantity of pints of milk = 5 pints.
=> 5 pints = 2 × 5 = 10 cups.
Conversion: 1 quarts = 4 cups.
Quantity of orange juice = 3 quarts.
=> 3 quarts = 4 × 3
= 12 cups.
Number of cups can be filled with smoothies = Quantity of orange juice + Quantity of pints of milk + Quantity of cups of pineapple juice
= 12 cups + 10 cups + 5 cups
= 27 cups.
Assessment Practice
Question 19.
Which equals 3 quarts?
A. 6 cups
B. 12 cups
C. 12 pints
D. 3 gallons
Answer:
3 quarts = 12 cups.
B. 12 cups
Explanation:
1 quarts = 4 cups.
3 quarts = 4 × 3 = 12 cups.
1 quart = 2 pint.
3 quarts = 2 × 3 = 6 pints.
1 quart = 0.25 gallon.
3 quarts = 3 × 0.25 = 0.75 gallon.
Question 20.
Select all the comparisons that are true.
☐ 4 cups < 4 pints
☐ 7 pints > 7 fluid ounces
☐ 2 gallons > 9 quarts
☐ 3 quarts < 14 cups
☐ 3 gallons < 18 pints
Answer:
All the comparisons that are true:
4 cups < 4 pints (TRUE)
7 pints > 7 fluid ounces (TRUE)
3 quarts < 14 cups (TRUE)
3 gallons < 18 pints (TRUE)
Explanation:
All the comparisons that are true:
☐ 4 cups < 4 pints (TRUE)
☐ 7 pints > 7 fluid ounces (TRUE)
☐ 2 gallons > 9 quarts (FALSE)
☐ 3 quarts < 14 cups (TRUE)
☐ 3 gallons < 18 pints (TRUE)
☐ 4 cups < 4 pints
1 pint = 2 cups.
4 cups < 4 pints
=> 4 × 2 = 8 cups < 4 pints.
☐ 7 pints > 7 fluid ounces
1 pint = 16 fluid ounces
=> 7 × 16 = 112 > 7 fluid ounces.
1 gallon = 4 quarts.
☐ 2 gallons > 9 quarts
=> 2 × 4 = 8 quarts > 9 quarts.
1 quarts = 4 cups.
☐ 3 quarts < 14 cups
=> 3 × 4 = 12 < 14 cups.
1 gallon = 8 pints.
3 gallons < 18 pints
=> 3 × 8 = 24 < 18 pints.
Lesson 13.3 Equivalence with Customary Units of Weight
Solve & Share
When Lori’s puppy, Bay, was born she weighed \(\frac{3}{8}\) pound. What was Bay’s weight in ounces? Solve this problem any way you choose.
I can … convert customary units of weight from one unit to another and recognize the relative size of different units.
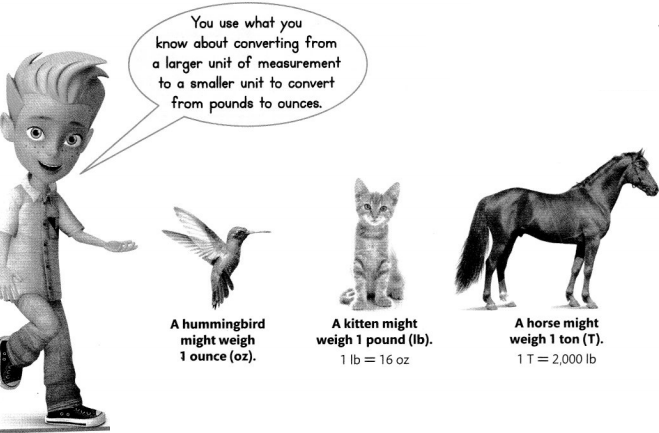
Look Back! Be Precise How did you know you needed to convert units to solve the problem above?
Answer:
Well, we need to know the units given in the problem to convert. Next we should find the units value into which, the value should be converted into and later convert into the required units to solve the problem asked above.
Essential Question
How Can You Convert from One Unit of Weight to Another?
Answer:
We have also learnt conversion of one unit to another. We can convert from One Unit of Weight to Another by knowing the value of the conversion unit and multiplying it.
For example:
We can convert kilogram into grams by multiplying the number of kilograms by 1000. To convert grams into kilograms, we divide the number of grams by 1000.
Visual Learning Bridge
Mark made dinner for his family using the ingredients shown. How many 6-ounce servings did Mark make?
Weight is how heavy an object is. Units of weight include ounces, pounds, and tons.
This table shows the relative sizes of customary units of weight. 1 pound is 16 times as heavy as 1 ounce.
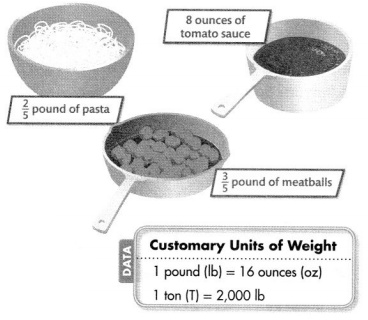
To convert the weight of the pasta and the meatballs to ounces, multiply each weight by 16.
Pasta:
2 × 16 = 32
= 6\(\frac{2}{5}\) ounces
Meatballs:
\(\frac{3}{5}\) × 16 = \(\frac{48}{5}\)
= 9\(\frac{3}{5}\) ounces
Add the weights of all the ingredients to find the total ounces.

The weight of all the ingredients is 24 ounces.
Divide to find s, the number of servings.
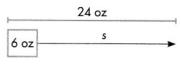
24 = 6 = s
s = 4
Mark made four 6-ounce servings.
Convince Me! Generalize How do you convert a larger unit of weight to a smaller unit of weight?
Answer:
We can convert a larger unit of weight to a smaller unit of weight by multiplying. To convert from a smaller unit to a larger one, divide.
Guided Practice
Do You Understand?
Question 1.
Would it make sense to describe the total weight of Mark’s dinner in tons? Why or why not?
Answer:
No, it does not makes sense to describe the total weight of Mark’s dinner in tons because it is not asked in the problem to find.
Do You Know How?
For 2-4, convert each unit.
Question 2.
9 tons = ________ pounds
Answer:
9 tons = ________ pounds.
Explanation:
Conversion: 1 ton = 2000 pounds.
9 tons = 2000 × 9
= 18000 pounds
Question 3.
\(\frac{3}{4}\) pound = _______ ounces
Answer:
\(\frac{3}{4}\) pound = ___12____ ounces
Explanation:
Conversion: 1 pound = 16 ounces.
\(\frac{3}{4}\) pound = 16 × \(\frac{3}{4}\)
= 12 ounces.
Question 4.
17 pounds = _________ ounces
Answer:
17 pounds = ___272______ ounces.
Explanation:
Conversion: 1 pound = 16 ounces.
17 pounds = 16 × 17
= 272 ounces.
Independent Practice
In 5-7, write > or < in each ![]() to compare the measures.
to compare the measures.
Question 5.
6 ounces ![]() 6 pounds
6 pounds
Answer:
6 ounces < 6 pounds.
Explanation:
6 ounces and 6 pounds.
Conversion: 1 pound = 16 ounces.
6 pounds = 16 × 6
= 96 ounces.
Question 6.
3 pounds ![]() 40 ounces
40 ounces
Answer:
3 pounds > 40 ounces.
Explanation:
3 pounds and 40 ounces.
Conversion: 1 pound = 16 ounces.
3 pounds = 16 × 3
= 48 ounces.
Question 7.
5,000 pounds ![]() 2 tons
2 tons
Answer:
5,000 pounds > 2 tons.
Explanation:
5,000 pounds and 2 tons.
Conversion: 1 ton = 2000 pounds.
2 tons = 2000 × 2
= 4000 pounds.
For 8-13, convert each unit.
Question 8.
15 pounds = ________ ounces
Answer:
15 pounds = ___240_____ ounces.
Explanation:
Conversion: 1 pound = 16 ounces.
15 pounds = 16 × 15
= 240 ounces.
Question 9.
7 tons = _______ pounds
Answer:
7 tons = _14000______ pounds.
Explanation:
Conversion: 1 ton = 2000 pounds.
7 tons = 2000 × 7
= 14000 pounds.
Question 10.
46 pounds = ________ounces
Answer:
46 pounds = __736______ounces.
Explanation:
Conversion: 1 pound = 16 ounces.
46 pounds = 16 × 46
= 736 ounces.
Question 11.
\(\frac{1}{8}\) pound = ________ ounces
Answer:
\(\frac{1}{8}\) pound = ____2____ ounces.
Explanation:
Conversion: 1 pound = 16 ounces.
\(\frac{1}{8}\) pound = 16 × \(\frac{1}{8}\)
= 2 ounces.
Question 12.
6 tons = _______ pounds
Answer:
6 tons = ___12000______ pounds.
Explanation:
Conversion: 1 ton = 2000 pounds.
6 tons = 2000 × 6
= 12000 pounds.
Question 13.
3 pounds = _______ ounces
Answer:
3 pounds = __48_____ ounces.
Explanation:
Conversion: 1 pound = 16 ounces.
3 pounds = 16 × 3
= 48 ounces.
For 14-15, complete each table.
Question 14.
Answer:
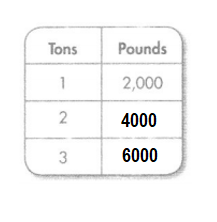
Explanation:
Conversion: 1 ton = 2000 pounds.
2 tons = 2000 × 2 = 4000 pounds.
3 tons = 2000 × 3 = 6000 pounds.
Question 15.
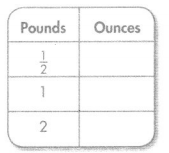
Answer:

Explanation:
Conversion: 1 pound = 16 ounces.
\(\frac{2}{4}\) pound = 16 × \(\frac{2}{4}\)
= 8 ounces.
1 pound = 16 ounces.
2 pounds = 16 × 2 = 32 ounces.
Problem Solving
For 16-19, use the line plot at the right.
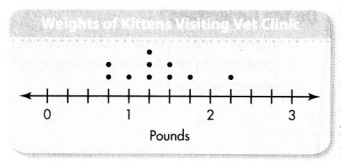
Question 16.
Be Precise What is the total weight in ounces of the three kittens that weight the least?
Answer:
Total weight in ounces of the three kittens that weight the least = 40 ounces.
Explanation:
Weight of Three kittens that weight the least = \(\frac{3}{4}\) pound + \(\frac{3}{4}\) pound + 1 pound.
= 2\(\frac{2}{4}\) pound.
Conversion: 1 pound = 16 ounces.
Total weight in ounces of the three kittens that weight the least = 2\(\frac{2}{4}\) pound = 16 × 2\(\frac{2}{4}\)
= 40 ounces.
Question 17.
Higher Order Thinking Two kittens had a total weight of 3\(\frac{1}{4}\) pounds. What could their individual weights have been?
Answer:
Their individual weights could be = 1\(\frac{2}{4}\) pounds + 1\(\frac{3}{4}\) pounds.
Explanation:
Weight of two kitten had a total weight of 3\(\frac{1}{4}\) pounds:
Their individual weights could be = 1\(\frac{2}{4}\) pounds + 1\(\frac{3}{4}\) pounds.
= 3\(\frac{1}{4}\) pounds.
Question 18.
Algebra How many more pounds did the heaviest kitten weigh than the lightest kitten?
Answer:
1\(\frac{2}{4}\) more pounds the heaviest kitten weights than the lightest kitten,
Explanation:
Weight of the heaviest kitten = 2\(\frac{1}{4}\) pounds.
Weight of the lightest kitten = \(\frac{3}{4}\) pounds.
Difference:
Weight of the heaviest kitten – Weight of the lightest kitten
= 2\(\frac{1}{4}\) pounds – \(\frac{3}{4}\) pounds
= 1\(\frac{2}{4}\) pounds.
Question 19.
Each of the greatest number of kittens weighed how many pounds?
Answer:
1\(\frac{1}{4}\) pounds is the greatest number of kittens weighed of 3\(\frac{3}{4}\) pounds.
Explanation:
Greatest number of kittens weighed = 3 × 1\(\frac{1}{4}\) pounds
= 3\(\frac{3}{4}\) pounds.
Question 20.
About how many pounds does this African elephant weigh? Complete the table to solve.

Answer:
This African elephant weights = 10000 pounds.

Explanation:
This African elephant weights = 5 tons.
Conversion: 1 ton = 2000 pounds.
=> 5 tons = 2000 × 5
= 10000 pounds.
Table :
\(\frac{2}{4}\) ton = 2000 × \(\frac{2}{4}\) = 1000 pounds.
1 ton = 2000 pounds.
2 ton = 2000 × 2 = 4000 pounds.
3 ton = 2000 × 3 = 6000 pounds.
4 ton = 2000 × 4 = 8000 pounds.
5 ton = 2000 × 5 = 10000 pounds.
Assessment Practice
Question 21.
Which is most likely to weigh 3 ounces?
A. A shoe
B. A large spider
C. A box of cerea!
D. A loaded pick-up truck
Answer:
A shoe is most likely to weigh 3 ounces.
A. A shoe
Explanation:
A. A shoe – 9.5 ounces.
B. A large spider – 5300 ounces.
C. A box of cereal – 12 ounces to 18 ounces.
D. A loaded pick-up truck – 64000 ounces.
Question 22.
Which comparison is true?
A. 7,000 pounds < 3 tons
B. 5 pounds > 85 ounces
C. 50 ounces > 3 pounds
D. 4 pounds < 60 ounces
Answer:
The following below comparison is true:
C. 50 ounces > 3 pounds.
Explanation:
A. 7,000 pounds < 3 tons (False)
Conversion: 1 ton = 2000 pounds.
=> 3 tons = 2000 × 3 = 6000 pounds.
B. 5 pounds > 85 ounces (False)
Conversion: 1 pound = 16 ounces.
=> 5 pounds = 16 × 5 = 80 ounces.
C. 50 ounces > 3 pounds (True)
=> 3 pounds = 16 × 3 = 48 ounces.
D. 4 pounds < 60 ounces (False)
=> 4 pounds = 16 × 4 = 64 ounces.
Lesson 13.4 Equivalence with Metric Units of Length
Solve & Share
Find the length of the marker shown in both centimeters and millimeters. Describe the relationship between the two units.
I can …convert metric units of length from one unit to another and recognize the relative size of different units.

Look Back! The length of Toby’s giant pencil is 25 centimeters. How could you find the length of his pencil in millimeters?
Answer:
We can find the length of his pencil in millimeter by using conversion of units into another required unit.
Length of his pencil in millimeters = 250 millimeters.
Explanation:
Length of Toby’s giant pencil = 25 centimeters.
Conversion: 1 centimeter = 10 millimeters.
Length of his pencil in millimeters = 25 centimeters = 10 × 25
= 250 millimeters.
Essential Question
How Can You Convert from One Metric Unit of Length to Another?
Answer:
To convert from one unit to another within the metric system usually means moving a decimal point. If you can remember what the prefixes mean, you can convert within the metric system relatively easily by simply multiplying or dividing the number by the value of the prefix
Visual Learning Bridge
For the standing long jump, Corey jumped 2 meters and Gary jumped 175 centimeters. Who jumped farther?

Step 1
Convert 2 meters to centimeters.
1 meter = 100 centimeters

Corey jumped 200 centimeters.
Step 2
Compare the lengths jumped.
200 centimeters is greater than 175 centimeters.
Corey jumped farther than Gary
Convince Me! Critique Reasoning Shayla says 5 kilometers are equal to 500 meters. Do you agree? Explain.
Answer:
Yes, I agree with Shayla saying ” 5 kilometers are equal to 500 meters.”
Explanation:
Conversion: 1 kilometer = 1000 meters.
5 kilometers = 1000 × 5 = 5000 meters.
Another Example!
Kendra and Lili measured the length of several rosebuds. The longest one Kendra measured was 2.4 centimeters long. The longest one Lili measured was 1.8 centimeters. Who measured the longest rosebud? Use a linear model to help explain.
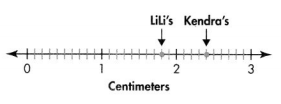
Since 2.4 cm > 1.8 cm, Kendra measured the longest rosebud.
Guided Practice
Do You Understand?
Question 1.
What metric unit would you use to measure the length of a field?
Answer:
The most common units that we use to measure length of a field in the metric system are the millimeter, centimeter, meter, and kilometer.
Do You Know How?
For 2-3, convert each unit.
Question 2.
5 kilometers = _______ meters
Answer:
5 kilometers = __5000_____ meters.
Explanation:
Conversion: 1 kilometer = 1000 meters.
5 kilometers = 1000 × 5
= 5000 meters.
Question 3.
75 centimeters = ________ millimeters
Answer:
75 centimeters = _____750_______ millimeters.
Explanation:
Conversion: 1 centimeters = 10 millimeters.
75 centimeters = 10 × 75
= 750 millimeters.
Independent Practice
In 4-6, tell what metric unit you would use to measure each.
Question 4.
The length of your math book
Answer:
Metric unit used to measure the length of your math book centimeter (cm).
Question 5.
The distance between cities
Answer:
Metric unit used to measure the distance between cities is Kilometers per hour.
Question 6.
The length of a fly
Answer:
Metric unit used to measure the length of a fly is meter.
For 7-8, complete each table.
Question 7.
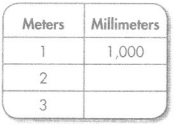
Answer:

Explanation:
Conversion: 1 meter = 1000 millimeter.
2 meter = 2 × 1000 = 2000 millimeter.
3 meter = 3 × 1000 = 3000 millimeter.
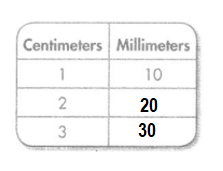
Question 8.

Answer:
Explanation:
Conversion: 1 centimeter = 10 millimeter.
2 centimeter = 10 × 2 = 20 millimeter.
3 centimeter = 10 × 3 = 30 millimeter.
Problem Solving
For 9-10, use the table at the right.

Question 9.
Be Precise The table shows the amount of rainfall students measured for a week. What was the total rainfall for the week, in millimeters?
Answer:
Total rainfall for the week, in millimeters = 110 millimeters.
Explanation:
Amount of rainfall on Monday = 3 cm.
Amount of rainfall on Tuesday = 0 cm.
Amount of rainfall on Wednesday = 1 cm.
Amount of rainfall on Thursday = 5 cm.
Amount of rainfall on Friday = 2 cm.
Total rainfall for the week = Amount of rainfall on Monday + Amount of rainfall on Tuesday + Amount of rainfall on Wednesday + Amount of rainfall on Thursday + Amount of rainfall on Friday
= 3 cm + 0 cm + 1 cm + 5 cm + 2 cm
= 11 cm.
Conversion: 1 cm = 10 mm.
Total rainfall for the week, in millimeters = Total rainfall for the week × 10
=> 11 × 10 = 110 millimeters.
Question 10.
How many more millimeters of rain fell on Thursday than on Monday and Wednesday combined?
Answer:
10 more millimeters of rain fell on Thursday than on Monday and Wednesday combined.
Explanation:
Amount of rainfall on Monday = 3 cm.
Amount of rainfall on Wednesday = 1 cm.
Amount of rainfall on Thursday = 5 cm.
Combine Rain fell on Monday and Wednesday = Amount of rainfall on Monday + Amount of rainfall on Wednesday
= 3 cm + 1 cm
= 4 cm.
Difference:
Amount of rainfall on Thursday – Combine Rain fell on Monday and Wednesday
= 5 cm – 4 cm
= 1 cm.
Conversion: 1 centimeter = 10 millimeter.
Difference in millimeter of rain fell on Thursday than on Monday and Wednesday combined = 1 centimeter = 10 millimeter.
Question 11.
Which is greater, 2,670 meters or 2 kilometers? Explain.
Answer:
2,670 meters is greater.
Explanation:
2,670 meters or 2 kilometers.
Conversion: 1 kilometer = 1000 meters.
2 kilometers = 1000 × 2 = 2000 meters.
Question 12.
Critique Reasoning Milo thinks 8 hours is greater than 520 minutes. Is Milo correct? Remember 1 hour is equal to 60 minutes.
Answer:
No, Milo is incorrect because 8 hours = 480 minutes less than 520 minutes.
Explanation:
Conversion: 1 Hour = 60 minutes.
8 hours = 60 × 8 = 480 minutes.
Question 13.
Algebra Leah ran around the track 8 times. She ran a total of 2,000 meters. How many meters equal 1 lap? Use the bar diagram to write an equation which can be used to find m, the meters in one lap.

Answer:
1 Lap = 400 meters.
Explanation:
Number of meters She ran = 2000m.
Number of times Algebra Leah ran around the track = 8.
Number of meters equal 1 lap = Number of meters She ran ÷ Number of times Algebra Leah ran around the track
= 2000 ÷ 8
= 400 meters.
1 Lap = 400 meters
Question 14.
Higher Order Thinking Signs are placed at the beginning and at the end of a 3-kilometer hiking trail. Signs are also placed every 500 meters along the trail. How many signs are along the trail? Explain.
Answer:
Total signs along the trail = 7.
Explanation:
Distance of Signs are placed at the beginning and at the end of a hiking trail = 3 kilometer.
Signs placed along the trail = 500 meters.
Conversion: 1 km = 1000 meters.
3 km = 1000 × 3 = 3000 meters.
Total signs along the trail = Distance of Signs are placed at the beginning and at the end of a hiking trail ÷ Signs placed along the trail + 1
= 3000 ÷ 500 + 1
= 6 + 1
= 7.
Assessment Practice
Question 15.
Select all the true statements.
☐ 14 meters = 1,400 centimeters
☐ 10 centimeters = 1,000 millimeters
☐ 55 kilometers = 5,500 meters
☐ 3 meters = 3,000 millimeters
☐ 5 meters = 500 centimeters
Answer:
All the true statements:
14 meters = 1,400 centimeters
55 kilometers = 5,500 meters
3 meters = 3,000 millimeters
5 meters = 500 centimeters
Explanation:
☐ 14 meters = 1,400 centimeters. (True)
Conversion: 1 meters = 100 centimeters.
14 meters = 10 × 14 = 1400 centimeters.
☐ 10 centimeters = 1,000 millimeters. (False)
Conversion: 1 centimeters = 10 millimeters.
10 centimeters = 10 × 10 = 100 millimeters.
☐ 55 kilometers = 5,500 meters. (True)
Conversion: 1 kilometers = 1000 meters.
55 kilometers = 1000 × 55 = 5500 meters.
☐ 3 meters = 3,000 millimeters. (True)
Conversion: 1 meter = 1000 millimeters.
3 meters = 1000 × 3 = 3000 millimeters.
☐ 5 meters = 500 centimeters. (True)
Conversion: 1 meter = 100 centimeters.
5 meters = 100 × 5 = 500 centimeters.
Question 16.
Select all the true statements.
☐ 3 meters > 3,000 centimeters
☐ 2 kilometers < 2,500 meters
☐ 4 centimeters > 38 millimeters
☐ 3.5 meters < 3.2 meters
☐ 5 kilometers < 5,200 meters
Answer:
All the true statements:
2 kilometers < 2,500 meters.
4 centimeters > 38 millimeters.
5 kilometers < 5,200 meters.
Explanation:
☐ 3 meters > 3,000 centimeters. (False)
Conversion: 1 meter = 100 centimeters.
3 meters = 100 × 3 = 300 centimeters.
☐ 2 kilometers < 2,500 meters . (True)
Conversion: 1 kilometers = 1000 meters.
2 kilometers = 1000 × 2 = 2000 meters.
☐ 4 centimeters > 38 millimeters. (True)
Conversion: 1 centimeters = 10 millimeters.
4 centimeters = 10 × 4 = 40 millimeters.
☐ 3.5 meters < 3.2 meters. ( False)
☐ 5 kilometers < 5,200 meters. (True)
Conversion: 1 kilometers = 1000 meters.
5 kilometers = 1000 × 5 = 5000 meters.
Lesson 13.5 Equivalence with Metric Units of Capacity and Mass
Solve & Share
Jenny has 3 liters of water. How many milliliters of water does she have, and what is the mass of the water in grams? Solve this problem any way you choose.
I can… convert metric units of capacity and mass from one unit to another and recognize the relative size of different units.

Look Back! Why did you need to convert units to solve the problem above?
Answer:
Well, it is the conversion between an amount in one unit to the corresponding amount in a desired unit using various conversion factors. This is valuable because certain measurements are more accurate or easier to find than others.
Essential Question
How Can You Convert from One Metric Unit of Capacity or Mass to Another?
Answer:
We convert from One Metric Unit of Capacity or Mass to Another, larger unit multiply, smaller unit divide.
Visual Learning Bridge
Louis needs 8 liters of apple juice. He has 5,000 milliliters of juice. Does Louis have enough apple juice?
Step 1
Find how many milliliters of apple juice Louis needs.
1 liter = 1,000 milliliters

Louis needs 8,000 milliliters of juice.
Step 2
Compare to find if Louis has enough apple juice.
8,000 milliliters > 5,000 milliliters
Louis does not have enough apple juice. How much more does he need?
8,000 – 5,000 = 3,000
Louis needs 3,000 milliliters more.
Convince Me! Be Precise Why did you need to convert liters to milliliters?
Answer:
We need to convert liters to milliliters because Louis needs milliliters of juice not liters.
Another Example!
How many grams of apples are needed to make 1 liter of apple juice?

1 kilogram = 1,000 grams
2 kilograms = 2 × 1,000 grams
= 2,000 grams
2,000 grams of apples make 1 liter of apple juice.
Guided Practice
Do You Understand?
Question 1.
What metric unit would you use to measure your mass? the amount of blood in your body? Explain.
Answer:
The gram and kilogram are two units used to measure mass in the metric system. the amount of blood in your body is measured in units of millimeters of mercury (mmHg).
Do You Know How?
For 2-3, convert each unit.
Question 2.
6 grams = _______ milligrams
Answer:
6 grams = ___6000____ milligrams.
Explanation:
Conversion: 1 gram = 1000 milligrams.
6 grams = 1000 × 6
= 6000 milligrams.
Question 3.
9 liters = _________ milliliters
Answer:
9 liters = ___9000______ milliliters.
Explanation:
Conversion: 1 gram = 1000 milligrams.
9 liters = 1000 × 9
= 9000 milliliters.
Independent Practice
In 4-6, tell what metric unit you would use to measure each.
Question 4.
Medicine in a pill
Answer:
Orally administered liquid medications should be dosed exclusively by using metric-based dosing with milliliters (ie, mL) to avoid confusion and dosing errors associated with common kitchen spoons
Question 5.
Ink in a pen
Answer:
Metric unit used to measure Ink in a pen is grams.
Question 6.
The mass of a pencil
Answer:
Metric unit used to measure the mass of a pencil is grams.
For 7-10, convert each unit.
Question 7.
5 kilograms = ________ grams
Answer:
5 kilograms = ___5000_____ grams.
Explanation:
Conversion: 1 kilograms = 1000 grams.
5 kilograms = 1000 × 5
= 5000 grams.
Question 8.
2 liters = _______ milliliters
Answer:
2 liters = ___2000______ milliliters.
Explanation:
Conversion: 1 liter = 1000 milliliters.
2 liters = 1000 × 2
= 2000 milliliters.
Question 9.
4 grams = _______ milligrams
Answer:
4 grams = _____4000______ milligrams.
Explanation:
Conversion: 1 gram = 1000 milligrams.
4 grams = 1000 × 4
= 4000 milligrams.
Question 10.
9 kilograms = ________ grams
Answer:
9 kilograms = _____9000______ grams.
Explanation:
Conversion: 1 kilogram = 1000 grams.
9 kilograms = 1000 × 9
= 9000 grams.
Problem Solving
Question 11.
Reasoning A cardboard box has a mass of 800 grams. When 4 books of equal mass are put into the box, the filled box has a mass of 8 kilograms. What is the mass of each book in grams? Explain.
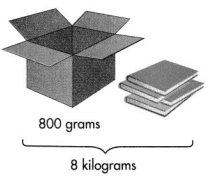
Answer:
The mass of each book in grams = 1800 grams.
Explanation:
Mass of a cardboard box has = 800 grams.
4 books of equal mass are put into the box, Mass of the filled box has = 8 kilograms.
Conversion: 1 kilogram = 1000 grams.
=> 8 kilograms = 1000 × 8 = 8000 grams.
The mass of each book in grams = Mass of the filled box has – Mass of a cardboard box has ÷ 4
= 8000 grams – 800 grams ÷ 4
= 7200 grams ÷ 4
= 1800 grams.
Question 12.
en Vision® STEM The Cape Hatteras Lighthouse was a kilometer from the shore in 1870. How far was the lighthouse from the shore in 1970? Explain.

Answer:
Distance of the lighthouse away from the shore in 1970 = 920 meters.
Explanation:
Distance of the Cape Hatteras Lighthouse from the shore in 1870 = 1 kilometer.
Conversion: 1 kilometer = 1000 meters.
Distance of the beach near the Cape Hatteras Lighthouse eroded = 8 meters each year.
Distance of the lighthouse away from the shore in 1970 = 1 kilometer – (Distance of the beach near the Cape Hatteras Lighthouse eroded × number of years from 1870 – 1970)
=1000 – (8 × 10)
= 1000 – 80
= 920 meters.
Question 13.
The mass of 4 large zucchini is about 2 kilograms. About how many grams will 1 large zucchini have?
Answer:
Number of grams will 1 large zucchini = 500 grams.
Explanation:
Mass of 4 large zucchini = 2 kilograms.
Conversion: 1 kilogram = 1000 grams.
=> 2 kilograms = 1000 × 2 = 2000 grams.
Number of zucchini = 4.
Number of grams will 1 large zucchini = Mass of 4 large zucchini ÷ Number of zucchini
= 2000 ÷ 4
= 500 grams.
Question 14.
Higher Order Thinking A small sofa has a mass of 30 kilograms. A pillow on the sofa has a mass of 300 grams. How many pillows would it take to equal the mass of the sofa?
Answer:
Number of pillows it take to equal the mass of the sofa = 100.
Explanation:
Mass of small sofa = 30 kilograms.
Conversion: 1 kilograms = 1000 grams.
=> 30 kilograms = 1000 × 30 = 30000 grams.
Mass of a pillow on the sofa = 300 grams.
Number of pillows it take to equal the mass of the sofa = Mass of small sofa ÷ Mass of a pillow on the sofa
= 30000 ÷ 300
= 100 .
Assessment Practice
Question 15.
Which shows a correct comparison?
A. 5 milliliters > 50 liters
B. 2 liters < 200 milliliters
C. 100 liters < 1,000 milliliters
D. 3,200 milliliters > 3 liters
Answer:
A correct comparison:
D. 3,200 milliliters > 3 liters
Explanation:
A. 5 milliliters > 50 liters. (False)
Conversion: 1 liter = 1000 milliliters.
=> 50 liters = 1000 × 50 = 50000 liters.
B. 2 liters < 200 milliliters. (False)
Conversion: 1 liter = 1000 milliliters.
=> 20 liters = 1000 × 2 = 2000 milliliters.
C. 100 liters < 1,000 milliliters. (False)
Conversion: 1 liter = 1000 milliliters.
=> 100 liters = 1000 × 100 = 100000 milliliters.
D. 3,200 milliliters > 3 liters. (True)
Conversion: 1 liter = 1000 milliliters.
=> 3 liters = 1000 × 3 = 3000 milliliters.
Question 16.
Write the missing numbers in the table.
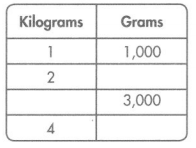
Answer:
Conversion: 1 kilograms = 1000 grams.
2 kilograms = 1000 × 2 = 2000 grams.
3 kilograms = 1000 × ?? = 3000 grams.
=> 3000 ÷ 1000 = 3.
4 kilograms = 1000 × 4 = 4000 grams.
Lesson 13.6 Solve Perimeter and Area Problems
Solve & Share
A can of paint is used to cover all 168 square feet of a wall. The wall is 8 feet high. Tape is placed along the top, bottom, and sides of the wall. What is the width of the wall? How much tape is needed? Solve this problem any way you choose.
I can … find the unknown length or width of a rectangle using a known area or perimeter.

Look Back! Describe the steps you would use to solve the problem.
Answer:
The steps used to solve the problem:
1. Collect the given complete information of the problem.
2. Find the width of the wall.
3. Find out the perimeter of the wall to find the how much tape to be needed.
.
Essential Question
How Can You Use Perimeter and Area to Solve Problems?
Answer:
The perimeter is the distance around the outside of an object. The perimeter is found by adding the lengths of all of the sides of the object together. Area is the size of the surface of the object or the total amount of space that the object covers.
Visual Learning Bridge
The state park shown has a perimeter of 36 miles. What is the area of the state park?
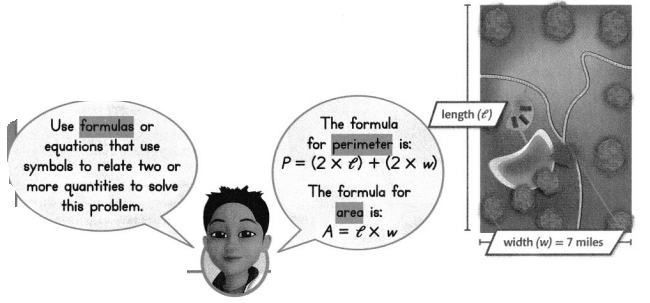
Step 1
Find the length of the state park.
Use the perimeter, 36 miles, and the width, 7 miles, to find the length.
Opposite sides of a rectangle are the same length, so multiply the width by 2. 7 × 2 = 14
Subtract 14 from the perimeter. 36 – 14 = 22
22 miles is the length of two sides of the park. Divide 22 by 2 to find the length of one side. 22 =2= 11
The length of the park is 11 miles.
Step 2
Find the area of the state park.
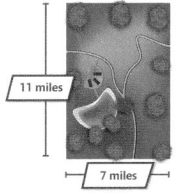
w = 7 miles
l = 11 miles
A = l × w
= 11 × 7
= 77
The area of the state park is 77 square miles,
Convince Me! Make Sense and Persevere If the area of another state park is 216 square miles, and the park has a width of 8 miles, what is the park’s length? What is the perimeter of this state park?
Answer:
Length of another state park = 27 miles.
Perimeter of this state park = 70 miles.
Explanation:
Area of the another state park = 216 square miles.
Width of another state park = 8 miles.
Length of another state park = L miles.
Area of the another state park = L × W = 216 square miles.
=> L × 8 = 216
=> L = 216 ÷ 8
=> L = 27 miles.
Perimeter of this state park = 2(L + W)
=> 2(27 + 8)
=> 2 × 35
= 70 miles.
Guided Practice
Do You Understand?
Question 1.
A sandbox is shaped like a rectangle. The area is 16 square feet. The side lengths are whole numbers. What are the possible dimensions of the sandbox? Do all possible dimensions make sense?
Answer:
The possible dimensions of the sandbox = (8miles and 2 miles) or (4miles and 4 miles).
Explanation:
Area of sandbox = 16 square feet.
The side lengths are whole numbers.
Let the Length of sandbox be L.
Width of sandbox be W.
Area of sandbox = L × W
=> 16 = L × W
=> 16 ÷ L = W.
or 16 ÷ W = L.
Length of sandbox and Width of sandbox dimensions can be 8 miles and 2 miles or 4 miles or 4 miles.
Question 2.
Write and solve an equation to find the width of a room if the length of the floor is 8 feet and the area of the room is 96 square feet.
Answer:
Width of the room = 12 feet.
Explanation:
Area of the room = 96 square feet.
Length of the floor = 8 feet.
Let Width of the room = W feet.
Area of the room = L × W = 96 square feet.
=> 8 × W = 96
=> W = 96 ÷ 8
=> W = 12 feet.
Do You Know How?
For 3-5, complete each calculation.
Question 3.
Find n. Perimeter = 46 in.
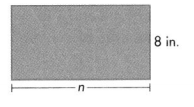
Answer:
Width of the rectangle = 15 inches.
Explanation:
Perimeter of the rectangle = 46 inches.
Length of the rectangle = 8 inches.
Width of the rectangle = n inches.
Perimeter of the rectangle = 2(L + W) = 46 inches.
=>2(8 + n) = 46
=> 16 + 2n = 46
=> 2n = 46 – 16
=> n = 30 ÷ 2
=> n = 15 inches.
Question 4.
Find n and A. Perimeter = 26 cm
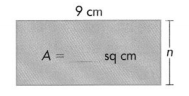
Answer:
Width of the rectangle = 4 cm.
Area of the rectangle = 36 sq cm.
Explanation:
Perimeter of the rectangle = 26 cm.
Length of the rectangle = 9 cm.
Width of the rectangle = n cm.
Perimeter of the rectangle = 2(L + W) = 26 cm.
=> 2(9 + n) = 26
=> 18 + 2n = 26
=> 2n = 26 – 18
=> n = 8 ÷ 2
=> n = 4 cm.
Area of the rectangle = L × w
= 9 × 4
= 36 square cm.
Question 5.
Find the perimeter.

Answer:
Perimeter of the square = 22 yards.
Explanation:
Side of the square = 5\(\frac{2}{4}\) yards.
Perimeter of the square = 4 × Side of square
= 4 × 5\(\frac{2}{4}\)
= 22 yards.
Independent Practice
For 6-9, find the missing dimension.
Question 6.
Find n.
Answer:
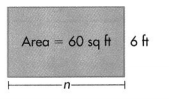
Width of the rectangle = 10 ft.
Explanation:
Area of the rectangle = 60 sq ft.
Length of the rectangle = 6 ft.
Width of the rectangle = n ft.
Area of the rectangle = L × W = 60 sq ft
=> 6 × n = 60
=> n = 60 ÷ 6
=> n = 10 ft.
Question 7.
Find n. Perimeter = 65 in.

Answer:
Width of the rectangle = 21 inches.
Explanation:
Perimeter of the rectangle = 65 inches.
Length of the rectangle = 11\(\frac{2}{4}\) inches.
Width of the rectangle = n inches.
Perimeter of the rectangle = 2(L + W) = 65 inches.
=> 2 (11\(\frac{2}{4}\) + n) = 65
=> 23 + 2n = 65
=> 2n = 65 – 23
=> n = 42 ÷ 2
=> n = 21 inches.
Question 8.
Find n. Perimeter = 84 yd
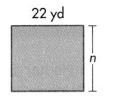
Answer:
Width of the rectangle = 20 yd.
Explanation:
Perimeter of the rectangle = 84 yd.
Length of the rectangle = 22 yd.
Width of the rectangle = n yd.
Perimeter of the rectangle = 2(L + W) = 84 yd.
=> 2 (22 + n) = 84
=> 44 + 2n = 84
=> 2n = 84- 44
=> n = 40 ÷ 2
=> n = 20 yd.
Question 9.
A rectangle has a length of 9 millimeters and an area of 270 square millimeters. What is the width? What is the perimeter?

Answer:
Width of the rectangle = 30 millimeters.
Perimeter of the rectangle = 78 millimeters.
Explanation:
Length of the rectangle = 9 millimeters.
Area of the rectangle = 270 square millimeters.
Width of the rectangle = w millimeters.
Area of the rectangle = L × W = 270 square millimeters.
=> 9 × w = 270
=> w = 270 ÷ 9
=> w = 30 millimeters.
Perimeter of the rectangle = 2(L+ W)
= 2(9 + 30)
= 2 × 39
= 78 millimeters.
Problem Solving

Question 10.
Greg built the picture frame shown to the right. It has a perimeter of 50\(\frac{2}{4}\) inches. How wide is the picture frame?
Answer:
Width of the picture frame = 10 inches.
Explanation:
Length of the picture frame = 15\(\frac{1}{4}\) inches.
Perimeter of the picture frame = 50\(\frac{2}{4}\) inches.
Let Width of the picture frame be w inches.
Perimeter of the picture frame = 2(L + W) = 50\(\frac{2}{4}\) inches.
=> 2(15\(\frac{1}{4}\) + w) = 50\(\frac{2}{4}\)
=> 30\(\frac{2}{4}\) + 2w = 50\(\frac{2}{4}\)
=> 2w = 50\(\frac{2}{4}\) – 30\(\frac{2}{4}\)
=> w = 20 ÷ 2
=> w = 10 inches.
Question 11.
Greg covered the back of the picture with a piece of felt. The picture is 17 inches shorter than the frame and 1\(\frac{1}{4}\) inch less in width. What is the area of the felt?
Answer:
Area of the felt = 70 inches.
Explanation:
Length of the picture frame = 15\(\frac{1}{4}\) inches.
Width of the picture frame = 10 inches.
Perimeter of the picture frame = 50\(\frac{2}{4}\) inches.
The picture is 17 inches shorter than the frame and 1\(\frac{1}{4}\) inch less in width.
=> Width of the felt = Width of the picture frame – 1\(\frac{1}{4}\) inch
=> 10 – 1\(\frac{1}{4}\)
=> 8\(\frac{3}{4}\) inches.
=> Perimeter of the picture frame – 17 inches = Perimeter of the felt.
=> 50\(\frac{2}{4}\) – 17 = Perimeter of the picture.
=> 33\(\frac{2}{4}\) inches = Perimeter of the picture.
Length of the felt = L inches.
Perimeter of the felt = 2(L + W)
33\(\frac{2}{4}\) = 2(L + 8\(\frac{3}{4}\) )
33\(\frac{2}{4}\) = 2L + 17\(\frac{2}{4}\)
33\(\frac{2}{4}\) – 17\(\frac{2}{4}\) = 2L
16 ÷ 2 = L
8 inches = L.
Area of the felt = L × W
= 8 × 8\(\frac{3}{4}\)
= 70 inches.
Question 12.
Al has a goal to read 2,000 pages over summer break. He has read 1,248 pages. How many more pages does Al need to read to reach his goal?
Answer:
Number of more pages Al needs to read to reach his goal = 752.
Explanation:
Number of pages Al has a goal to read = 2000.
Number of pages he has read = 1248.
Number of more pages Al needs to read to reach his goal = Number of pages Al has a goal to read – Number of pages he has read
= 2000 – 1248
= 752.
Question 13.
The area of a tabletop is 18 square feet. The perimeter of the same table is 18 feet. What are the dimensions of the tabletop?
Answer:
Dimensions of the tabletop (L and W) are:
(9 feet and 2 feet) or (6 feet and 3 feet) or (2 feet and 9 feet) or (3 feet and 6 feet)
Explanation:
Area of a tabletop = 18 square feet.
Perimeter of a tabletop = 18 feet.
Area of a tabletop = L × W = 18 sq feet.
=> L = 18 ÷ W
or W = 18 ÷ L.
Dimensions of the tabletop are:
(9 feet and 2 feet) or (6 feet and 3 feet) or (2 feet and 9 feet) or (3 feet and 6 feet)
Question 14.
Construct Arguments Amy and Zach each have 24 feet of fencing for their rectangular gardens. Amy makes her fence 6 feet long. Zach makes his fence 8 feet long. Whose garden has the greater area? How much greater? Explain.
Answer:
Amy garden has the greater area than Zach garden by 4 sq ft.
Explanation:
Perimeter of the rectangular garden fencing Amy and Zach each have = 24 feet.
Length of rectangular garden fence Zach makes = 8 feet.
Length of rectangular garden fence Amy makes = 6 feet.
Width of rectangular garden fence Amy makes = W feet.
Perimeter of the rectangular garden Amy makes = 2(L + W) = 24 feet.
=> 2(6 + W) = 24
=> 12 + 2W = 24
=> 2W = 24 – 12
=> W = 12 ÷ 2
=> W = 6 feet.
Area of the rectangular garden Amy makes = Length of rectangular garden fence Amy makes × Width of rectangular garden fence Amy makes
= 6 × 6
= 36 sq ft.
Length of rectangular garden fence Zach makes = 8 feet.
Width of rectangular garden fence Zach makes = w feet.
Perimeter of the rectangular garden Zach makes = 2(L + W) = 24 feet.
=> 2(8 + w) = 24
=> 16 + 2w = 24
=> 2w = 24 – 16
=> w = 8 ÷ 2
=> w = 4 feet.
Area of the rectangular garden Zach makes = Length of rectangular garden fence Zach makes × Width of rectangular garden fence Zach makes
= 8 × 4
= 32 sq ft.
Difference in areas of Zach and Amy rectangular gardens :
Area of the rectangular garden Amy makes – Area of the rectangular garden Zach makes
= 36 sq ft – 32 sq ft
= 4 sq ft.
Question 15.
Higher Order Thinking Nancy made a table runner that has an area of 80 square inches. The length and width of the table runner are whole numbers. The length is 5 times greater than the width. What are the dimensions of the table runner?
Answer:
The dimensions of the table runner:
Length of the table = 40 inches.
Width of the table = 8 inches.
Explanation:
Area of the table runner which Nancy made = 80 square inches.
The length is 5 times greater than the width.
Let the Length of the table be L inches.
=>L = 5W
Width of the table be W inches.
Area of the table runner = Length of the table × Width of the table = 80 square inches.
=> 5W × W = 80
=> 2W = 80 ÷ 5
=> 2W = 16
=> W = 16 ÷ 2
=> W = 8 inches.
Length of the table = 5W = 5 × 8 = 40 inches.
Assessment Practice
Question 16.
The rectangle has an area of 144 square centimeters. Which is its perimeter?

A. 26 cm
B. 48 cm
C. 52 cm
D. 72 cm
Answer:
Perimeter of the rectangle = 52 cm.
C. 52 cm
Explanation:
Area of the rectangle = 144 square centimeters.
Length of the rectangle = 8 cm.
Width of the rectangle = W cm
Area of the rectangle = L × W = 144 square centimeters.
=> 8 × W = 144
=> W = 144 ÷ 8
=> W = 18 cm.
Perimeter of the rectangle = 2(L + W )
= 2 (8 + 18)
= 2 × 26
= 52 cm.
Lesson 13.7 Problem Solving
Precision
Solve & Share
Mr. Beasley’s science class wants to decorate one wall in the classroom like an underwater scene. They use sheets of blue poster board that are 2 feet long and 2 feet wide. How many sheets of blue poster board are used to cover the entire area of the wall? Use math words and symbols to explain how you solve.
I can … be precise when solving math problems.
Thinking Habits
Be a good thinker! These questions can help you.
- Am I using numbers, units, and symbols appropriately?
- Am I using the correct definitions?
- Am I calculating accurately?
- Is my answer clear?
Look Back! Be Precise How can calculating the area of the whole wall and the area of one sheet of poster board help you determine the total number of sheets of poster board needed to cover the entire area of the wall?
Answer:
The wall is to be covered by the sheets so, it is required for calculating the area of the whole wall and the area of one sheet of poster board help you determine the total number of sheets of poster board needed to cover the entire area of the wall.
Essential Question
How Can You Be Precise When Solving Math Problems?
Answer:
We can Precise When Solving Math Problems by the following the below steps:
- Teach with Intention.
- Use Practice Sheets Appropriately.
- Use Best Practice Math Strategies and Instruction.
- Use Problems with Multiple Solutions.
- Differentiation is Critical.
Visual Learning Bridge
Piper has a fish tank and wants to cover all four sides \(\frac{6}{10}\) of the way to the top with clear plastic for insulation. She measures and finds the dimensions shown. How much plastic does Piper need? Use math words and symbols to explain how to solve.
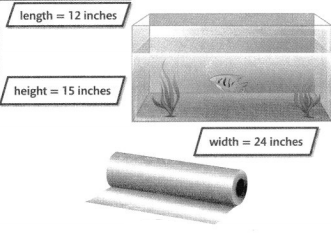
What do you need to know so you can solve the problem?
I need to find how much plastic is needed for the fish tank. I need to be precise in my calculations and explanation.
How can I be precise in solving this problem?
I can
- correctly use the information given.
- calculate accurately.
- decide if my answer is clear and appropriate.
- use the correct units.
Here’s my thinking.
The height of the plastic is \(\frac{6}{10}\) times 15 inches.
\(\frac{6}{10}\) × 15 = \(\frac{90}{10}\) or 9
The plastic is 9 inches high.
Front and back: A = 9 × 24
A = 216 square inches
Each side: A = 9 × 12
A = 108 square inches
Add: 216 + 216 + 108 + 108 = 648 square inches
Piper needs 648 square inches of plastic.
Convince Me! Be Precise How did you use math words and numbers to make your explanation clear?
Answer:
To justify a solution, we need to be able to use appropriate mathematical language to give reasons for the particular approach used to solve a problem. Any time we produce a ‘solution’ in an attempt to solve a problem, that ‘solution’ needs to be justified.
Guided Practice
Be Precise
Jeremy uses \(\frac{2}{3}\) yard of tape for each box he packs for shipping. How many inches of tape does Jeremy need to pack 3 boxes?

Question 1.
How can you use the information given to solve the problem?
Answer:
We can use the information given to solve the problem for :
- Defining the problem.
- Generating alternatives.
- Evaluating and selecting alternatives.
- Implementing solutions.
Question 2.
How many inches of tape does Jeremy need to pack 3 boxes? Explain.
Answer:
Number of inches of tape Jeremy needs to pack 3 boxes = 72 inches.
Explanation:
Jeremy uses \(\frac{2}{3}\) yard of tape for each box he packs for shipping. How many inches of tape does Jeremy need to pack 3 boxes?
Length of the tape Jeremy uses to tape each box he packs for shipping = \(\frac{2}{3}\) yard.
Number of tapes Jeremy needs to pack 3 boxes = Length of the tape Jeremy uses to tape each box he packs for shipping × 3
= \(\frac{2}{3}\) × 3
= 2 yards.
Conversion: 1 yard = 36 inches.
Number of inches of tape Jeremy needs to pack 3 boxes = Number of tapes Jeremy needs to pack 3 boxes × 36 inches
= 2 × 36
= 72 inches.
Question 3.
Explain why you used the units you did in your answer.
Answer:
Units are important because without proper measurement and units to express them, we can never express physical laws precisely just from qualitative reasoning.
Independent Practice
Be Precise
Mrs. Reed collects shells. Each shell in her collection weighs about 4 ounces. Her collection weighs about 12 pounds in all. About how many shells are in Mrs. Reed’s collection? Use Exercises 4-6 to solve.
Question 4.
How can you use the information given to solve the problem?
Answer:
We can use the information given to solve the problem for :
- Defining the problem.
- Generating alternatives.
- Evaluating and selecting alternatives.
- Implementing solutions.
Question 5.
What is the total weight of Mrs. Reed’s shell collection, in ounces?
Answer:
Total weight of her collection in ounces = 192 ounces.
Explanation:
Weight of each shell in Mrs. Reed’s collection = 4 ounces.
Total weight of her collection = 12 pounds.
Conversion : 1 pound = 16 ounces.
Total weight of her collection in ounces = 12 pounds
= 16 × 12 = 192 ounces.
Question 6.
How many shells are in Mrs. Reed’s shell collection?
Answer:
48 shells are in Mrs. Reed’s shell collection.
Explanation:
Weight of each shell in Mrs. Reed’s collection = 4 ounces.
Total weight of her collection = 12 pounds.
Conversion : 1 pound = 16 ounces.
Total weight of her collection in ounces = 12 pounds
= 16 × 12 = 192 ounces.
Number of shells are in Mrs. Reed’s collection = Total weight of her collection ÷ Weight of each shell in Mrs. Reed’s collection
= 192 ÷ 4
= 48.
Problem Solving
Performance Task
Making Thank You Cards Tanesha is making cards by gluing 1 ounce of glitter on the front of the card and then making a border out of ribbon. She makes each card the dimensions shown. How much ribbon does Tanesha need?

Question 7.
Reasoning What quantities are given in the problem and what do the numbers mean?
Answer:
Quantities are given in the problem:
Quantity of glitter used for making Thank You Cards by Tanesha = 1 ounce.
Length of the card = 9 cm.
Width of the card = 85 mm.
Number mean the amount of quantity measured and measurements of the cards.
Question 8.
Reasoning What do you need to find?
Answer:
We need to find how much quantity of ribbon Tanesha needs.
Question 9.
Model with Math What are the hidden questions that must be answered to solve the problem? Write equations to show how to solve the hidden questions.
Answer:
The hidden questions that must be answered to solve the problem is that we need the length of the ribbon required for which we should find out the perimeter of the card and convert the units.
Quantity of glitter used for making Thank You Cards by Tanesha = 1 ounce.
Length of the card = 9 cm.
Conversion: 1 cm = 10 mm.
Width of the card = 85 mm.
Perimeter of the card = 2(Length of the card + Width of the card)
Question 10.
Be Precise How much ribbon does Tanesha need? Use math language and symbols to explain how you solved the problem and computed accurately.

Answer:
Length of the ribbon required = 350 mm.
Explanation:
Quantity of glitter used for making Thank You Cards by Tanesha = 1 ounce.
Length of the card = 9 cm.
Conversion: 1 cm = 10 mm.
=> 9 cm = 10 × 9 = 90 mm.
Width of the card = 85 mm.
Perimeter of the card = 2(Length of the card + Width of the card)
= 2(90 + 85)
= 2 × 175
= 350 mm.
Question 11.
Reasoning What information was not needed in the problem?
Answer:
Quantity of glitter used for making Thank You Cards by Tanesha = 1 ounce. This information was not needed in the problem.
Topic 13 Fluency Practice Activity
Find a Match
Work with a partner. Point to a clue. Read the clue.
Look below the clues to find a match. Write the clue letter in the box next to the match.
Find a match for every clue.
Clues
A. The sum is between 2,000 and 2,500.
B. The difference is exactly 10,000.
C. The sum is exactly 6,000.
D. The difference is exactly 4,500.
E. The sum is exactly 16,477.
F. The sum is between 5,500 and 5,600.
G. The difference is between 1,000 and 2,000.
H. The difference is between 8,000 and 9,000.

Answer:
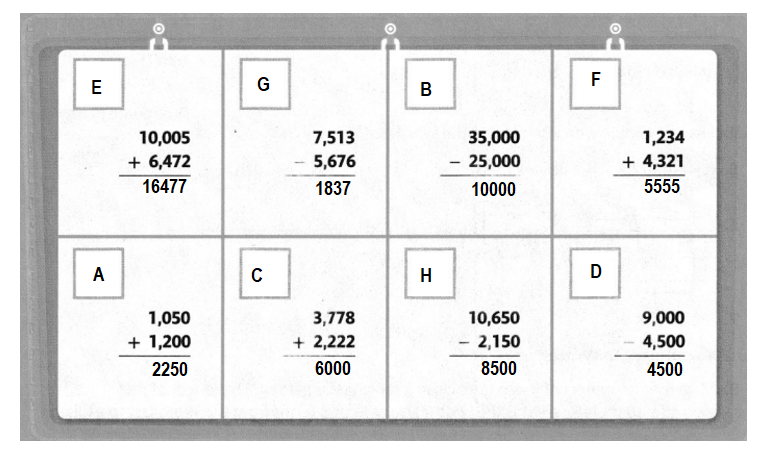
Explanation:
10005+6472 = 16477.
1050+1200=2250.
7513-5676=1837.
3778+2222 = 6000.
35000-25000=10000.
10650-2150=8500.
1234+4321=5555.
9000-4500=4500.
Topic 13 Vocabulary Review
Understand Vocabulary
Word List
- area
- capacity
- centimeter (cm)
- cup (c).
- formula
- gallon (gal)
- gram (g)
- kilogram (kg)
- kilometer (km)
- liter (L)
- mass
- meter (m)
- milligram (mg)
- milliliter (mL)
- millimeter (mm)
- ounce (oz)
- perimeter
- pint (pt)
- pound (lb)
- quart (qt)
- ton (T)
- weight
- fluid ounce (fl oz)
Question 1.
Cross out the units that are NOT used to measure length.
centimeter (cm)
pint (pt)
pound (lb)
kilogram (kg)
Answer:
The units that are NOT used to measure length:
centimeter (cm)
pint (pt)
pound (lb)
kilogram (kg) X
Question 2.
Cross out the units that are NOT used to measure capacity.
millimeter (mm)
ounce (oz)
gallon (gal)
milliliter (mL)
Answer:
The units that are NOT used to measure capacity:
millimeter (mm) X
ounce (oz)
gallon (gal)
milliliter (mL)
Question 3.
Cross out the units that are NOT used to measure weight.
cup (c)
liter (L)
meter (m)
ton (T)
Answer:
The units that are NOT used to measure weight:
cup (c)
liter (L)
meter (m) X
ton (T)
Question 4.
Cross out the units that are NOT used to measure mass.
liter (L)
kilometer (km)
milligram (mg)
quart (qt)
Answer:
The units that are NOT used to measure mass:
liter (L)
kilometer (km) X
milligram (mg)
quart (qt)
Label each example with a term from the Word List.
Question 5.
![]() 2 × 4 = 8 square units _________
2 × 4 = 8 square units _________
Answer:
2 × 4 = 8 square units __Area_______.
Question 6.
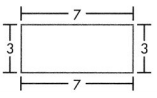 3 + 7 + 3 + 7 = 20 units __________
3 + 7 + 3 + 7 = 20 units __________
Answer:
3 + 7 + 3 + 7 = 20 units ___perimeter_______.
Question 7.
Area = l × w _________
Answer:
Area = l × w __Formula_______.
Use Vocabulary in Writing
Question 8.
Mike uses 24 meters of fence to enclose a rectangular garden. The length of the garden is 10 meters. What is the width? Use at least 3 terms from the Word List to explain.
Answer:
Width of the garden = 2 meters.
Explanation:
Length of fence to enclose a rectangular garden Mike uses = 24 meters.
Perimeter of the rectangular garden Mike uses = 24 meters.
Length of the garden =10 meters.
Width of the garden = W meters.
Formula:
Perimeter of the rectangular garden = 2(L + W) = 24 meters.
=> 2(10 + W) = 24
=> 20 + 2W = 24
=> 2W = 24- 20
=>W = 4 ÷ 2
=> W = 2 meters.
Topic 13 Reteaching
Set A pages 481-492
Customary units can be used when measuring length, capacity, and weight.

Remember when converting from a larger unit to a smaller unit, multiply. Use the conversion charts to help solve.
Question 1.
9 yards = _________ inches
Answer:
9 yards = ____324_____ inches.
Explanation:
1 yard = 36 inches.
9 yards = 36 × 9
= 324 inches.
Question 2.
5 miles = _________ yards
Answer:
5 miles = ____8800_______ yards.
Explanation:
1 mile = 1760 yards.
5 miles = 1760 × 5
= 8800 yards.
Question 3.
215 yards = _________ feet
Answer:
215 yards = ____645_____ feet.
Explanation:
1 yard = 3 feet.
215 yards = 3 × 215
= 645 feet.
Question 4.
9 pints = _________ fluid ounces
Answer:
9 pints = ___144______ fluid ounces.
Explanation:
1 pint = 16 fluid ounces.
9 pints = 16 × 9
= 144 fluid ounces.
Question 5.
372 quarts = _________ cups
Answer:
372 quarts = ___1488______ cups.
Explanation:
1 quart = 4 cups.
372 quarts = 4 × 372
= 1488 cups.
Question 6.
1,620 gallons = _________ pints
Answer:
1,620 gallons = _____12960_______ pints.
Explanation:
1 gallon = 8 pints.
1,620 gallons = 8 × 1620
= 12960 pints.
Question 7.
9 pounds = _________ ounces
Answer:
9 pounds = ___144______ ounces.
Explanation:
1 pound = 16 ounces.
9 pounds = 16 × 9
= 144 ounces.
Question 8.
5 tons = _________ pounds
Answer:
5 tons = ____10000_____ pounds.
Explanation:
1 ton = 2000 pounds.
5 tons = 2000 × 5
= 10000 pounds.
Question 9.
12 feet = _________ inches
Answer:
12 feet = ___144______ inches.
Explanation:
1 feet = 12 inches.
12 feet = 12 × 12
= 144 inches.
Set B pages 493-500
Metric units can be used to measure length, capacity, and mass.

Remember metric units can be converted using multiples of 10. Use the conversion charts to help.
Question 1.
9 kilometers = _________ meters
Answer:
9 kilometers = ___9000______ meters.
Explanation:
1 kilometer = 1000 meters.
9 kilometers = 1000 × 9
= 9000 meters.
Question 2.
55 centimeters = _________ millimeters
Answer:
55 centimeters = ____550_____ millimeters.
Explanation:
1 centimeter = 10 millimeters.
55 centimeters = 10 × 55
= 550 millimeters
Question 3.
2 meters = _________ centimeters
Answer:
2 meters = ___200______ centimeters.
Explanation:
1 meter = 100 centimeters.
2 meters = 100 × 2
= 200 centimeters.
Question 4.
9 liters = _________ milliliters
Answer:
9 liters = ___9000______ milliliters.
Explanation:
1 liter = 1000 milliliters.
9 liters = 1000 × 9
= 9000 milliliters.
Question 5.
4 grams = _________ milligrams
Answer:
4 grams = ___4000______ milligrams.
Explanation:
1 gram = 1000 milligrams.
4 grams = 1000 × 4
= 4000 milligrams.
Question 6.
5 kilograms = _________ grams
Answer:
5 kilograms = ___5000______ grams.
Explanation:
1 kilogram = 1000 grams.
5 kilograms = 1000 × 5
= 5000 grams.
Question 7.
8 kilograms = _________ grams
Answer:
8 kilograms = _____8000______ grams.
Explanation:
1 kilograms = 1000 grams.
8 kilograms = 1000 × 8
= 8000 grams.
Question 8.
5 grams = _________ milligrams
Answer:
5 grams = ___5000______ milligrams.
Explanation:
1 gram = 1000 milligrams.
5 grams = 1000 × 5
= 5000 milligrams.
Set C pages 501-504
The perimeter of Ted’s pool is 16 yards. The pool is 3 yards wide. He has 150-square feet of plastic. Does Ted have enough plastic to cover the pool?
Use the formula for perimeter to find the length. Substitute the numbers you know.
Perimeter = (2 × l) + (2 × w)
16 = (2 × l) + (2 × 3)
l = 5
The length of the pool is 5 yards.
3 yards wide × 3 = 9 feet wide
5 yards long × 3 = 15 feet long
Find the area of the pool.
A = 15 × 9
A = 135
The area of the pool is 135 square feet. 135 < 150, so Ted has enough plastic to cover the pool.
Remember to label your answer with the appropriate unit.
Question 1.
Find n.
P = 108 inches
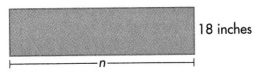
Answer:
Width of rectangle = 36 inches.
Explanation:
Perimeter of rectangle = 108 inches.
Length of rectangle = 18 inches.
Width of rectangle = n inches.
Perimeter of rectangle = 2(L + W) = 108 inches.
=> 2 (18 + n) = 108
=> 36 + 2n = 108
=> 2n = 108 -36
=>n = 72 ÷ 2
=> n = 36 inches.
Question 2.
Find the area.
P = 26 m
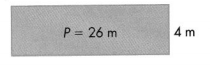
Answer:
Area of rectangle = 36 sq m.
Explanation:
Perimeter of rectangle = 26 m.
Length of rectangle = 4m.
Width of rectangle = Wm.
Perimeter of rectangle = 2(L + W) =26m.
=>2(4 + W) = 26
=> 8 + 2W = 26
=> 2W = 26 – 8
=>W = 18 ÷ 2
=> W = 9m.
Area of rectangle = L × W
= 4 × 9
= 36 sq m.
Question 3.
Find the perimeter of the square.
Answer:
Perimeter of square = 10 yards.
Explanation:
Side of square = 2\(\frac{2}{4}\) yards.
Perimeter of square = 4 × Side
= 4 × 2\(\frac{2}{4}\)
= 10 yards.
Set D pages 505-508
Think about these questions to help you be precise.
Thinking Habits
- Am I using numbers, units, and symbols appropriately?
- Am I using the correct definitions?
- Am I calculating accurately?
- Is my answer clear?

Remember to give an explanation that is clear and appropriate.
A puppy pen is 4 feet wide and 5 feet long.
Question 1.
Is 21 square feet of fabric large enough to make a mat for the pen? Explain.
Answer:
Yes, it is enough to make a mat for the pen because it requires 20 sq feet for the mat and its 1 sq feet more than required.
Explanation:
Width of the puppy pen = 4 feet.
Length of the puppy pen = 5 feet.
Area of the puppy pen = L × W
= 5 × 4
= 20 sq feet.
Question 2.
Puppy fencing comes in sizes that are 12 feet, 24 feet, and 30 feet in length. Which length would be the best for the pen? How much, if any, will have to be left over? Explain.
Answer:
24 feet length would be the best for the pen and it leaves with 6 feet of more.
Explanation:
Puppy fencing comes in sizes that are 12 feet, 24 feet, and 30 feet in length.
Width of the puppy pen = 4 feet.
Length of the puppy pen = 5 feet.
=> Perimeter of fencing required for puppy pen = 2(L + W)
=> 2(5 + 4)
=> 2 × 9
=> 18 feet.
Difference:
18 feet – 12 feet = 6 feet.
24 feet – 18 feet = 6 feet.
30 feet – 18 feet = 12 feet.
Topic 13 Assessment Practice
Question 1.
A window is 5 feet long. What is the length of the window in inches?
Answer:
Length of the window = 60 inches.
Explanation:
Length of the window = 5 feet.
Conversion: 1 feet = 12 inches.
5 feet = 12 × 5
= 60 inches.
Question 2.
Mrs. Warren bought 6 liters of lemonade for a party. How many milliliters of lemonade did she buy?
A. 9,000 milliliters
B. 6,000 milliliters
C. 3,000 milliliters
D. 1,200 milliliters
Answer:
6000 milliliters of lemonade did she buy.
B. 6,000 milliliters.
Explanation:
Quantity of lemonade Mrs. Warren bought for a party = 6 liters.
Conversion: 1 liter = 1000 milliliters.
= 1000 × 6
= 6000 milliliters.
Question 3.
Select the equivalent measurement for each measurement on the left.
Answer:
Explanation:
Conversion:
1 feet = 12 inches.
9 feet = 12 × 9 = 108 inches.
1 cup = 8 fluid ounces.
9 cups = 8 × 9 = 72 fluid ounces.
1 ton = 2000 lb.
4 tons = 2000 × 4 = 8000 lb.
1 yard = 36 inches.
4 yards = 36 × 4 = 144 inches.
Question 4.
A picnic table is 9 feet long and 3 feet wide. Write and solve an equation to find the area of the rectangular surface of the table.
Answer:
Area of the rectangular surface of the table = 27 square feet.
Explanation:
Length of a picnic table = 9 feet.
Width of a picnic table = 3 feet.
Area of the rectangular surface of the table = L × W
= 9 × 3
= 27 square feet.
Question 5.
The Girl’s Club is making muffins. Mindy’s recipe calls for 3 cups of buttermilk. Josie’s recipe calls for 20 fluid Ounces of buttermilk. Georgia’s recipe calls for 1 pint of buttermilk. Whose recipe calls for the most buttermilk? Explain.
Answer:
Georgia’s recipe calls for the most buttermilk because its most between 0.05 cup and 3 cups.
Explanation:
Quantity of buttermilk Mindy’s recipe calls for = 3 cups.
Quantity of buttermilk Josie’s recipe calls for = 20 fluid Ounces.
Quantity of buttermilk Georgia’s recipe calls for = 1 pint .
Conversion:
1 cup = 8 fluid ounces.
=> 20 fluid Ounces = 1 ÷ 20 = 0.05 cups.
1 pint = 2 cups.
Question 6.
Andrea ran 4 kilometers over the weekend. How many meters did Andrea run?
Answer:
Number of meters Andrea run =4000 meters.
Explanation:
Distance Andrea ran over the weekend = 4 kilometers.
Conversion: 1 kilometer = 1000 meters.
Number of meters Andrea run = 1000 × 4
= 4000 meters.
Question 7.
Choose numbers from the box to complete the table. Some numbers will not be used.
Answer:
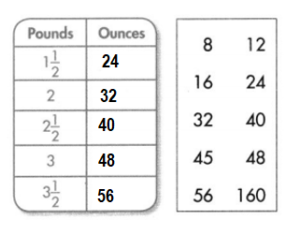
Explanation:
Conversion:
1 pound = 16 ounces.
1\(\frac{2}{4}\) pounds = 16 × 1\(\frac{2}{4}\)
= 24 ounces.
2 pounds = 16 × 2
= 32 ounces.
2\(\frac{2}{4}\) pounds = 16 × 2\(\frac{2}{4}\)
= 40 ounces.
3 pounds = 16 × 3
= 48 ounces.
3\(\frac{2}{4}\) pounds = 16 × 3\(\frac{2}{4}\) pounds
= 56 ounces.
Question 8.
Select each correct equation.
☐ 1l = 100 mL
☐ 1 kg = 1,000 g
☐ 4 yd = 14 ft
☐ 15 cm = 150 mm
☐ 1 gal = 13 cups
Answer:
Correct equation:
1 kg = 1,000 g.
Explanation:
☐ 1l = 100mL (False)
☐ 1 kg = 1,000 g (True)
☐ 4 yd = 14 ft (False)
☐ 15 cm = 150 mm (False)
☐ 1 gal = 13 cups (False)
Conversion:
1 l = 100 mL. (False)
1 kg = 1000 g.
1 yd = 3 ft
=> 4 yd = 3 × 4 = 12 ft.
1 cm = 100 mm.
=> 15 cm = 100 × 15 = 1500 mm.
1 gal = 16 cups.
Question 9.
Morgan rode her bike 2 kilometers from her house to her friend’s house. From her friend’s house, she rode 600 meters in all going to and from the library. Then she rode back home. How many meters did Morgan bike in all?
Answer:
Distance in meters she rode in all = 2600 meters.
Explanation:
Distance Morgan rode her bike from her house to her friend’s house = 2 kilometers.
Distance From her friend’s house, she rode in all going to and from the library = 600 meters.
Distance in meters she rode in all = Distance Morgan rode her bike from her house to her friend’s house + Distance From her friend’s house, she rode in all going to and from the library
= 2 kilometers + 600 meters
Conversion: 1 km = 1000 m.
=> 2 kilometers = 1000 × 2 = 2000 meters.
=> 2000 + 600 = 2600 meters.
Question 10.
Which statement is true about the bedrooms in the drawings below?

A. Erin’s room has a greater area than Steve’s room.
B. Steve’s room has a greater perimeter than Erin’s room.
C. They both have the same perimeter.
D. None of the above
Answer:
Statement is true about the bedrooms in the drawings below:
C. They both have the same perimeter.
Explanation:
Length of Steve’s room = 9 ft.
Width of Steve’s room = 8 ft.
Area of Steve’s room = L × W
= 9 × 8
= 72 square feet.
Perimeter of Steve’s room = 2(L + W)
= 2(9 + 8)
= 2 × 17
= 34 feet.
Length of Erin’s room = 10 ft.
Width of Erin’s room = 7 ft.
Area of Erin’s room = L × W
= 10 × 7
= 70 square feet.
Perimeter of Erin’s room = 2(L + W)
= 2(10 + 7)
= 2 × 17
= 34 feet.
A. Erin’s room has a greater area than Steve’s room. (False)
B. Steve’s room has a greater perimeter than Erin’s room. (False)
C. They both have the same perimeter. (True)
D. None of the above. (False)
Question 11.
Tim has 3 meters of yarn. How many centimeters of yarn does Tim have?
Answer:
33.34 centimeters of yarn Tim has.
Explanation:
Length of yarn Tim has = 3 meters.
Conversion: 1 m = 100 cm.
3 meters = 100 ÷ 3
= 33.34 centimeters.
Question 12.
Mrs. Li’s classroom is 34 feet wide and 42 feet long.

A. What is the area of the classroom?
Answer:
Area of Mrs. Li’s classroom = 1428 square feet.
Explanation:
Length of Mrs. Li’s classroom = 34 feet.
Width of Mrs. Li’s classroom = 42 feet.
Area of Mrs. Li’s classroom = L × W
= 34 × 42
= 1428 square feet.
B. How much area is taken up by the objects in the classroom? How much area is left for the students’ desks? Write and solve equations to find the area.
Answer:
Area left for the students’ desks = 1194 square feet.
Explanation:

Area of Mrs.Li’s desk = 8 square feet.
Area of Fish tank = 6 square feet.
Area of Math center = 100 square feet.
Area of Reading center = 120 square feet.
Area taken up by the objects in the classroom = Area of Mrs.Li’s desk + Area of Fish tank + Area of Math center + Area of Reading center
= 8 + 6 + 100 + 120
= 234 square feet.
Area left for the students’ desks = Area of Mrs. Li’s classroom – Area taken up by the objects in the classroom
= 1428 square feet – 234 square feet
= 1194 square feet.
Question 13.
Select the equivalent measurement for each measurement on the left.
Answer:
Explanation:
Conversion:
1g = 1000 mg.
=> 3 g = 1000 × 3 = 3000 mg.
1kg = 1000 g.
=> 3 kg = 1000 × 3 = 3000 g.
1L = 1000 mL.
=> 3 L = 1000 × 3 = 3000 mL.
1m = 1000 mm.
=> 3 m = 1000 × 3 = 3000 mm.
Topic 13 Performance Task
Watermelons Kasia grows watermelons.
Question 1.
Kasia plants her watermelons in rows. Kasia’s watermelon field has a perimeter of 71\(\frac{1}{3}\) yards and is 14\(\frac{2}{3}\) yards wide. Each row is yard wide and the rows will be planted 2 yards apart.
Part A
What is the length of Kasia’s field? Explain.
Answer:
The length of Kasia’s field = 14\(\frac{2}{3}\) yards because its given in the problem.
Explanation:
The length of Kasia’s field = 14\(\frac{2}{3}\) yards.
Part B
What is the area of Kasia’s field? Complete the table to convert the length to feet. Be sure to use the correct units on your answer. Explain.
Answer:
Area of Kasia’s field = 308 square yards.
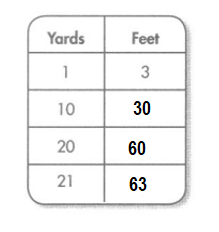
Explanation:
Length of Kasia’s field = 14\(\frac{2}{3}\) yards.
Width of Kasia’s field = W yards.
Perimeter of Kasia’s field = 71\(\frac{1}{3}\) yards.
Perimeter of Kasia’s field = 2(L + W) = 71\(\frac{1}{3}\) yards.
=> 2 (14\(\frac{2}{3}\) + W) = 71\(\frac{1}{3}\)
=> 28\(\frac{1}{3}\) + 2W = 71\(\frac{1}{3}\)
=> 2W = 71\(\frac{1}{3}\) – 29\(\frac{1}{3}\)
=> W = 42 ÷ 2
=> W = 21 yards.
Area of Kasia’s field = L × W
= 14\(\frac{2}{3}\) × 21
= 308 square yards.

Conversion: 1 yard = 3 feet.
10 yards = 3 × 10 = 30 feet.
20 yards = 3 × 20 = 60 feet.
21 yards = 3 × 21 = 63 feet.
Part C
How many rows can Kasia plant? Explain.
Answer:
Number of rows Kasia plant = 154.
Explanation:
Number of rows Kasia plant = 2.
Length of each row = 1 yard.
Width of the rows will be planted = 2 yards.
Area of Kasia’s field = 308 square yards.
Number of rows Kasia plant = Area of Kasia’s field ÷ Width of the rows will be planted
= 308 ÷ 2
= 154.
Question 2.
Use the information in the Watermelon table.

Part A
If there are twenty-eight 8-ounce servings in a 20-pound watermelon, how many pounds does the rind weigh? Explain.
Answer:
Quantity of rind in pounds = 2 pounds.
Explanation:
Quantity of watermelon = 20 pounds.
Quantity of watermelon servings = 288 ounces.
Conversion: 1 pound = 16 ounces.
=> 20 pounds = 16 × 20 = 320 ounces.
Quantity of rind = Quantity of watermelon – Quantity of watermelon servings
= 320 – 288
= 32 ounces.
Conversion: 1 pound = 16 ounces.
=> 32 ounces = 1 × 32 ÷ 16
= 32 ÷ 16 = 2 pounds.
Part B
How many cups of fruit does Kasia get from a 20-pound watermelon? Explain. Show your computations. Do not include the weight of the rind.
Answer:
Number of cups of fruit does Kasia get from a 20-pound watermelon = 40\(\frac{2}{4}\) cups.
Explanation:
Quantity of watermelon = 20 pounds.
Quantity of rind in pounds = 2 pounds.
Quantity of watermelon Kasia gets in pounds = Quantity of watermelon – Quantity of rind in pounds
= 20 – 2
= 18 pounds.
Conversion: 1 pound = 2\(\frac{1}{4}\) cups
Number of cups of fruit does Kasia get from a 20-pound watermelon =
=> 18 pounds = 2\(\frac{1}{4}\) × 18
=> 40\(\frac{2}{4}\) cups.
Question 3.
Use the information from the Watermelon and Nutrition picture to answer the question.

How many more milligrams of fiber than potassium are in a serving of watermelon? Explain.
Answer:
730 mg more milligrams of fiber than potassium are in a serving of watermelon.
Explanation:
Quantity of serving of fiber = 1 gram.
Conversion:
1g = 1000 mg
Quantity of serving of potassium = 270 milligram.
Difference:
Quantity of serving of fiber – Quantity of serving of potassium
= 1000 – 270
= 730 mg.