Conjugate Complex Numbers are the numbers that can be obtained by changing the sign of the imaginary part of the complex number. Complex numbers are the combination of both real numbers and imaginary numbers. The basic expression for the complex numbers is z= p + iq. In the above expression, ‘p’ is a real number and the ‘iq’ is an imaginary number. The value of ‘i’ is equal to √(-1.)An imaginary part of the complex numbers is denoted by either ‘i’ or ‘j’. For example, the complex number is 1 + 3i where 1 is a real number and 3i is an imaginary number.
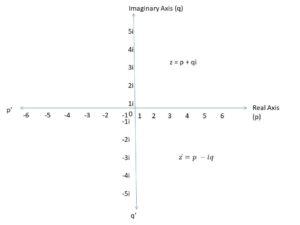
We can find out the conjugate number for every complex number. Yes, the conjugate complex number changes the sign of the imaginary part and there is no change in the sign of the real numbers. The conjugate complex number is denoted by\(\overline {z}\) or z*.
The conjugate complex number of z is \(\overline {z}\) or z*= p – iq.
For example,
- The conjugate complex number of 1 + 3i is \(\overline {z}\) = 1 – 3i.
- The conjugate complex number of 2 + 8i is \(\overline {z}\) = 2 – 8i.
- The conjugate complex number of 10 + 5i is \(\overline {z}\) = 10 – 5i.
- The complex conjugate number of 0.24 + 1.32i is \(\overline {z}\) = 0.24 – 1.32i.
Also, See:
Graphical Representation of the Conjugate Complex Number
Properties of a Conjugate Complex Numbers
The basic properties of the conjugate complex numbers are mentioned below. They are
(i) \(\overline {z}\) = z
Proof: z is a complex number. that is z = p + iq.
The conjugate complex number z is \(\overline {z}\) = p – iq.
Again, the conjugate of \(\overline {z}\) is z = p + iq.
Hence, \(\overline {z}\) = z is proved.
(ii) (z1 + z2) ̅ = (z1) ̅ + (z2) ̅
Proof: If z1 = p + iq and z2 = r + is.
Then, z1 + z2 = p + iq + r + is.
z1 + z2= (p + r) + i(q + s).
The conjugate of z1 + z2 is {z1 + z2} ̅ = (p + r) – i(q + s) ———(1).
The conjugate of z1 is {z1} ̅ = p – iq.
The conjugate of z2 is {z2} ̅ = r – is.
Now, z1+ z2= p – iq + r – is.
= (p + r) – i(q + s) ——-(2).
Finally, equation (1) = equation (2). (z1 + z2) ̅ = (z1) ̅ + (z2) ̅
(iii) (z1 – z2) ̅ = {z1} ̅ – {z2} ̅
Proof: If z1 = p + iq and z2 = r + is.
Then, z1 – z2 = (p + iq) –(r + is).
z1 – z2 = (p + iq – r – is)
z1 – z2 = (p – r) – i(q – s).
The conjugate of z1 – z2 is (z1 – z2) ̅ = (p – r) + i(q – s) ———(1).
The conjugate of z1 is z1 ̅= p – iq.
The conjugate of z2 is z2 ̅=r – is.
Now, z1̅- z2̅= p – iq –(r – is).
= p – iq – r + is.
= (p – r) – i(q – s) ——-(2).
Finally, equation (1) = equation (2). That is (z1 – z2) ̅ = z1̅- z2̅
(iv) (z1z2)= z1z2
Proof: If z1= p + iq and z2 = r + is.
Then, z1*z2 = (p + iq) * ( r + is) = pr + ips + iqr + (i)^2 qs.
i^2 = -1.
Apply the i^2 value in the above equation.
Then, we will get z1z2 = pr + i(ps + qr) – qs.
z1z2 = (pr – qs) +i(ps + qr).
The conjugate of z1z2 is (z1z2) ̅ = (pr – qs) – i(ps + qr) ———(1).
The conjugate of z1 is (z1) ̅ = p – iq.
The conjugate of z2 is (z2) ̅ = r – is.
= (p –iq) (r – is).
= pr –ips –iqr + i^2qs.
=pr – i(ps + qr) – qs.
= (pr – qs) – i(ps + qr) ———(2).
Finally, equation (1) is equal to equation (2).
(z1z2)= {z1} {z2}
(v)(z1//z2) = {z1} {z2} if z2 is not equal to zero.
Proof: (z1//z2)= {z1}. {1/z2}
We can write it as {z1} {1/z2}={z1}/ {z2}
Hence, It is proved as {(z1//z2)}= {z1}/ {z2}
(vi) |\(\overline {z}\)| = |z|
Proof: if z = p + iq.
Then conjugate of z is \(\overline {z}\) = p – iq.
|\(\overline {z}\)|= √(p^2+(-q)^2)=√(p^2+q^2) ——-(1).
|z| = √(p^2+(q)^2) ——-(2).
So, equation (1) is equal to equation (2).
Hence, |\(\overline {z}\)| = |z| is proved.
(vii) z\(\overline {z}\)=|z|^2.
Proof: if z = p + iq, then the conjugate of z is \(\overline {z}\)= p – iq.
z\(\overline {z}\)= (p + iq) ( p – iq).
= (p^2 – ipq + ipq –(iq)^2).
= p^2 –(i)^2q^2.
i^2 = -1.
Then, z\(\overline {z}\)=p^2+q^2 ———(1).
|z| = √(p^2+q^2).
|z|^2 = (√(p^2+q^2)))^2 = p^2 + q^2 ——-(2).
Equation (1) is equal to equation (2).
So, z\(\overline {z}\)=|z|^2 is proved.
(viii) z^-1 = {z/|z|2}, where z is not equal to zero.
Proof: The given information is
z^-1 = {z/|z|2}
we can write it as 1 / z = {z/|z|2}
So, |z|^2 = z\(\overline {z}\).
It is proved in the above property.
So, z^-1 = {z/|z|2} is proved.
Key Points of Conjugate Complex Numbers
- z + \(\overline {z}\)= 2 real parts of (z).
- z – \(\overline {z}\)= 2 imaginary parts of (z).
Solved Examples of Conjugate Complex Number
1. Find the conjugate of the complex number z = (2 + 3i) (2 + 5i)?
Solution: The given complex number is z = (2 + 3i) (2 + 5i).
z =4 + 10i + 6i + 15(i)^2.
Substitute (i)^2 = -1 in the above expression. Then we will get
z= 4 + 16i – 15 = -11 + i16.
Now, the conjugate of the complex number z is
\(\overline {z}\)= -11 – i16.
Therefore, the conjugate of the complex number z = (2 + 3i) (2 + 5i) is equal to -11 – i16.
2. Find the conjugate of the complex number z = (1 + 3i) / (1 – 3i)?
Solution: The given complex number is z = (1 + 3i) / (1 – 3i).
Multiply the numerator and denominator with the (1 + 3i). That is,
z = (1 + 3i) (1 + 3i) / ( 1 – 3i) (1 + 3i).
z = (1 + 3i)^2 / (1)^2 – (3i)^2.
(a + b)^2 = a^2 + 2ab + b^2—–(1).
a^2 – b^2 = (a + b) (a – b)—–(2).
Substitute the equation (1) and (2) in the complex number z. That is,
z = 1 + 2(3i) + (3i)^2 / (1 + 3i) (1 – 3i).
z = 1 + 6i -9 / 1 – 3i + 3i -9i^2. {i^2 = -1}.
z = -8 + 6i / 1+9.
z = – 8 + 6i / 10.
The conjugate of complex number z is \(\overline {z}\)= – 8 – 6i / 10.
3. Find the Conjugate of the complex number 4 + 10i and explain the real and imaginary numbers?
Solution: The given information is
The complex number is 4 + 10i.
The conjugate of the complex number 4 + 10i is 4 – 10i.
Here, the real number is 4 and the imaginary number is 10i.
4. Find the conjugate of the complex number (2x + 3yi)(2x + 20yi) and identify the real and imaginary numbers?
Solution: As per the given information
The complex number is (2x + 3yi) (2x + 20yi).
(2x + 3yi) (2x + 20yi) = 4x^2 + 40xyi + 6xyi + 60y^2(i)^2.
(2x + 3yi) ( 2x + 20yi) = 4x^2 + i46xy – 60y^2. {where i=-1}.
(2x + 3yi) ( 2x + 20yi) = (4x^2 – 60y^2) + i46xy.
The conjugate of complex number (4x^2 – 60y^2) + i46xy is (4x^2 – 60y^2) – i46xy.
The real number of the complex number is (4x^2 – 60y^2).
The imaginary number of the complex number is i46xy.
5. Evaluate the expression (3 + 5i) – (8 + 2i) and find the conjugate of the expression?
Solution: The given expression is (3 + 5i) – (8 + 2i).
Expand the expression 3 + 5i – 8 – 2i.
-5 + 3i.
By evaluating the expression (3 + 5i) – ( 8 + 2i) is equal to – 5 + 3i.
The conjugate of the expression – 5 + 3i is – 5 – 3i.
6. If z = 3 + 2i, then find the z\(\overline {z}\)?
Solution: The given complex number is z = 3 + 2i.
The conjugate of the complex number z is \(\overline {z}\)= 3 – 2i.
z\(\overline {z}\)= (3 + 2i)(3 – 2i).
z\(\overline {z}\)= 9 – 6i + 6i – 4(i)^2 {if i^2 = -1}.
z\(\overline {z}\)= 9 – 4(-1).
z\(\overline {z}\)= 9 + 4 = 13.
Therefore, z\(\overline {z}\) is equal to 13 and it is a real number.