Hey guys are you in search of diverse opportunities to develop your problem-solving skill? We have provided the best solution to it, just practice Big Ideas Math Grade 7 Answer Key for Chapter 4 Equations and Inequalities. This Big Ideas 7th Grade Math Chapter 4 Equations and Inequalities Answer Key is designed in a fun-learning way like mathematical practices through engaging activities such as games, literature-based exercises, and others. So, check out Big Ideas Math Answers Grade 7 Chapter 4 Equations and Inequalities Answer Key to prepare effectively by clearing all your doubts while practicing.
Big Ideas Math Book 7th Grade Answer Key Chapter 4 Equations and Inequalities
This is a free and user-friendly student edition of Big Ideas Math Book Grade 7 Answer Key Chapter 4 Equations and Inequalities lesson wise details are included below in PDF links. So, you are notified to improve their math, problem-solving skills by referring to these chapter-wise Big Ideas Math Answers Grade 7 Chapter 4 Equations and Inequalities. Also, you can make use of these Big Ideas Math Book 7th Grade Chapter 4 Equations and Inequalities Answer Key for Homework Help & complete all your assignments properly.
Performance
- Equations and Inequalities STEAM Video/Performance
- Equations and Inequalities Getting Ready for Chapter 4
Lesson: 1 Solving Equations Using Addition or Subtraction
- Lesson 4.1 Solving Equations Using Addition or Subtraction
- Solving Equations Using Addition or Subtraction Homework & Practice 4.1
Lesson: 2 Solving Equations Using Multiplication or Division
- Lesson 4.2 Solving Equations Using Multiplication or Division
- Solving Equations Using Multiplication or Division Homework & Practice 4.2
Lesson: 3 Solving Two-Step Equations
Lesson: 4 Writing and Graphing Inequalities
- Lesson 4.4 Writing and Graphing Inequalities
- Writing and Graphing Inequalities Homework & Practice 4.4
Lesson: 5 Solving Inequalities Using Addition or Subtraction
- Lesson 4.5 Solving Inequalities Using Addition or Subtraction
- Solving Inequalities Using Addition or Subtraction Homework & Practice 4.5
Lesson: 6 Solving Inequalities Using Multiplication or Division
- Lesson 4.6 Solving Inequalities Using Multiplication or Division
- Solving Inequalities Using Multiplication or Division Homework & Practice 4.6
Lesson: 7 Solving Two-Step Inequalities
Chapter: 4 – Equations and Inequalities
- Equations and Inequalities Connecting Concepts
- Equations and Inequalities Chapter Review
- Equations and Inequalities Practice Test
- Equations and Inequalities Cumulative Practice
Equations and Inequalities STEAM Video/Performance
STEAM Video
Space Cadets
Inequalities can be used to help determine whether someone is qualified to be an astronaut. Can you think of any other real-life situations where inequalities are useful?
Watch the STEAM Video “Space Cadets.” Then answer the following questions. Tori and Robert use the inequalities below to represent requirements for applying to be an astronaut, where height is measured in inches and age is measured in years.


Question 1.
Can you use equations to correctly describe the requirements? Explain your reasoning.
Answer:
Yes, we can use equations to correctly describe the requirements.
Explanation:
You can take the requirements as variables and their limit as constants. So that you can use equations to correctly describe the requirements.
Question 2.
The graph shows when a person who recently had vision correction surgery can apply to be an astronaut. Explain how you can determine when they had the surgery.
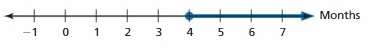
Answer:
The person had surgery exactly 4 months ago.
Explanation:
We can say that he had eye vision correction surgery 4 months from now because the point on the graph is at 4 and the line represents months.
Performance Task
Distance and Brightness of the Stars
After completing this chapter, you will be able to use the concepts you learned to answer the questions in STEAM Video Performance Task. You will be given information about the celestial bodies below.

You will use inequalities to calculate the distances of stars from Earth and to calculate the brightnesses, or apparent magnitudes, of several stars. How do you think you can use one value to describe the brightnesses of all the stars that can be seen from Earth? Explain your reasoning.
Answer:
I can take the value of brightness of all the stars that can be seen from Earth as variables. And each start brightness is assigned to that variable. Based on those stars brightness you will put an inequality symbol in between those variables.
Equations and Inequalities Getting Ready for Chapter 4
Chapter Exploration
Question 1.
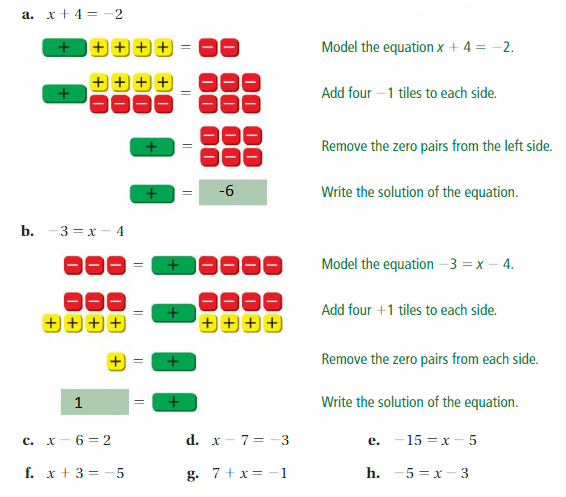
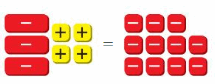
Work with a partner. Use algebra tiles to model and solve each equation. 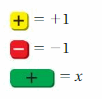

Answer:
Question 2.
WRITE GUIDELINES
Work with a partner. Use your models in Exercise 1 to summarize the algebraic steps that you use to solve an equation.
Answer:
The + symbol in the yellow box represents adding 1, – symbol in the red box represents subtracting 1, + in the green box represents the variable. So, you have to represent the given equation in the form of these symbols and do calculations to get the answer.
Vocabulary
The following vocabulary terms are defined in this chapter. Think about what each term might mean and record your thoughts.
![]()
Lesson 4.1 Solving Equations Using Addition or Subtraction
EXPLORATION 1
Using Algebra Tiles to Solve Equations
Work with a partner.
a. Use the examples to explain the meaning of each property.

Are these properties true for equations involving negative numbers? Explain your reasoning.
b. Write the four equations modeled by the algebra tiles. Explain how you can use algebra tiles to solve each equation. Then find the solutions.
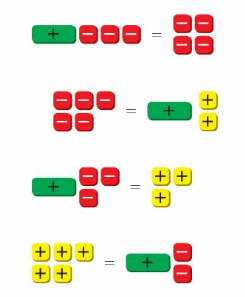

c. How can you solve each equation in part(b) without using algebra tiles?
Answer:
a. x = -1
Yes, algebraic properties are true for equations involving negative numbers.
b. x = -1, x = -7, x = 6, x = 7
Explanation:
a. x = 1 – 2
x = -1
b. x – 3 = -4
x = -4 + 3 = -1
-5 = x + 2
x = -5 – 2 = -7
x – 3 = 3
x = 3 + 3 = 6
5 = x – 2
x = 5 + 2 = 7
4.1 Lesson
Try It
Solve the equation. Check your solution.
Question 1.
p – 5 = -2
Answer:
p = 3
Explanation:
p – 5 = -2
Add 5 to both sides
p – 5 + 5 = -2 + 5
p = 3
Substitute p = 3 in p – 5 = -2
3 – 5 = -2
Question 2.
w + 13.2 = 10.4
Answer:
w = -2.8
Explanation:
w + 13.2 = 10.4
Subtract 13.2 from both sides
w + 13.2 – 13.2 = 10.4 – 13.2
w = -2.8
Putting w = -2.8 in w + 13.2 = 10.4
-2.8 + 13.2 = 10.4
Question 3.
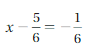
Answer:
x = 4/6
Explanation:
Adding 5/6 to both sides
x – 5/6 + 5/6 = -1/6 + 5/6
x = (-1 + 5)/6
x = 4/6
Putting x = 4/6 in x – 5/6 = -1/6
4/6 – 5/6 = -1/6
Try It
Question 4.
A bakery has a profit of $120.50 today. This profit is $145.25 less than the profit P yesterday. Write an equation that can be used to find P.
Answer:
P = $120.50 + $145.25
P = $265.75
Explanation:
Today profit = $120.50
$120.50 = – $145.25 + yesterday profit
$120.50 = -$145.25 + P
P = $120.50 + $145.25
P = $265.75
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
SOLVING AN EQUATION
Solve the equation. Check your solution.
Question 5.
c – 12 = -4
Answer:
c = 8
Explanation:
Add 12 to both sides
c – 12 + 12 = -4 + 12
c = 8
8 – 12 = -4
Question 6.
k + 8.4 = -6.3
Answer:
k = -14.7
Explanation:
Subtracting 8.4 from both sides
k + 8.4 – 8.4 = -6.3 – 8.4
k = -14.7
-14.7 + 8.4 = -6.3
Question 7.

Answer:
w = 5/3
Explanation:
Adding 7/3 on both sides
-2/3 + 7/3 = w – 7/3 + 7/3
(-2 + 7)/3 = w
w = 5/3
-2/3 = 5/3 – 7/3
Question 8.
WRITING
Are the equations m + 3 = -5 and m – 4 = -12 equivalent? Explain.
Answer:
Yes, both equations are equivalent.
Explanation:
m + 3 = -5 and m – 4 = -12
m = -5 – 3 and m = -12 + 4
m = -8 and m = -8
Question 9.
WHICH ONE DOESN’T BELONG?
Which equation does not belong with the other three? Explain your reasoning.

Answer:
x + 1 = -5
Explanation:
x + 3 = -1
x = -1 – 3 = -4
x + 1 = -5
x = -5 – 1 = -6
x – 2 = -6
x = -6 + 2 = -4
x – 9 = -13
x = -13 + 9 = -4
By solving all equations, we get solution as -4, but for x + 1 = -5, we get solution as -6.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 10.
You have $512.50. You earn additional money by shoveling snow. Then you purchase a new cell phone for $249.95 and have $482.55 left. How much money do you earn shoveling snow?
Answer:
You earn $220 by shoveling snow.
Explanation:
Let us take additional money earned by shoveling snow as x.
The total money you spend = $249.95
$512.50 + x – $249.95 = $482.55
$262.55 + x = $482.55
x = $482.55 – $262.55
x = $220
So, the money earned at shoveling snow is $220
Question 11.
DIG DEEPER!
You swim 4 lengths of a pool and break a record by 0.72 second. The table shows your time for each length compared to the previous record holder. How much faster or slower is your third length than the previous record holder?
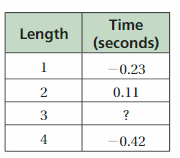
Answer:
1.26 seconds faster is my third length than the previous record holder.
Explanation:
Let us take the record at the third length as x.
So, -0.23 + 0.11 + x – 0.42 = 0.72
-0.54 + x = 0.72
x = 0.72 + 0.54
x = 1.26
So, the record at third length is 1.26 seconds.
Solving Equations Using Addition or Subtraction Homework & Practice 4.1
Review & Refresh
Factor out the coefficient of the variable term.
Question 1.
4x – 20
Answer:
4(x – 5)
Explanation:
Take 4 as common factor out.
4x – 20 = 4(x – 5)
Question 2.
-6y – 18
Answer:
-6y – 18 = -6(y + 3)
Explanation:
Take -6 as common factor out.
-6y – 18 = -6(y + 3)
Question 3.
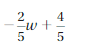
Answer:
-2/5 w + 4/5 = 2/5(-w + 2)
Explanation:
Take 2/5 as common factor
-2/5 w + 4/5 = 2/5(-w + 2)
Question 4.
0.75z – 6.75
Answer:
0.75z – 6.75 = 0.75(z – 6)
Explanation:
Take 0.75 as common factor
0.75z – 6.75 = 0.75(z – 6)
Multiply or divide.
Question 5.
-7 × 8
Answer:
-7 × 8 = -56
Explanation:
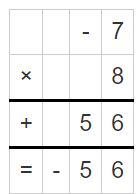
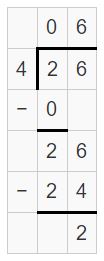
Question 6.
6 × (-12)
Answer:
6 × (-12) = -72
Explanation:
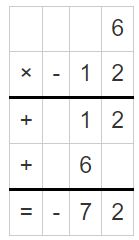
Question 7.
18 ÷ (-2)
Answer:
18 ÷ (-2) = -9
Explanation:
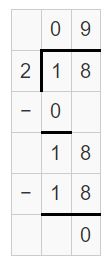
Question 8.
-26 ÷ 4
Answer:
-26 ÷ 4 = -6.5
Explanation:
Question 9.
A class of 144 students voted for a class president. Three-fourths of the students voted for you. Of the students who voted for you, \(\frac{5}{9}\) are female. How many female students voted for you?
A. 50
B. 60
C. 80
D. 108
Answer:
The number of female students voted for you is 60
Explanation:
The total number of students in class = 144
Three-fourths of the students voted for you = 3/4 x 144 = 36 x 3 = 108
Out of 108, 5/9 are female = 5/9 x 108 = 12 x 5 = 60
Therefore, the number of female students voted for you is 60.
Concepts, Skills, & Problem Solving
USING ALGEBRA TILES
Solve the equation using algebra tiles. Explain your reasoning. (See Exploration 1, p. 127.)
Question 10.
6 + x = 4
Answer:
x = -2
Explanation:
6 + x = 4
Subtract 6 from both sides
6 + x – 6 = 4 – 6
x = -2
Question 11.
x – 3 = = -5
Answer:
x = -2
Explanation:
Add 3 to both sides
x – 3 + 3 = -5 + 3
x = -2
Question 12.
-7 + x = -9
Answer:
x = -2
Explanation:
Add 7 to both sides
-7 + x + 7 = -9 + 7
x = -2
SOLVING AN EQUATION
Solve the equation. Check your solution.
Question 13.
a – 6 = 13
Answer:
a = 19
Explanation:
Add 6 to both sides
a – 6 + 6 = 13 + 6
a = 19
Substituting a= 19 in a – 6 = 13
19 – 6 = 13
Question 14.
-3 = z – 8
Answer:
z = 5
Explanation:
Add 8 to both sides.
-3 + 8 = z – 8 + 8
5 = z
Substituting z = 5 in -3 = z – 8
-3 = 5 – 8
Question 15.
-14 = k + 6
Answer:
k = -20
Explanation:
Subtract 6 from both sides
-14 – 6 = k + 6 – 6
-20 = k
Substituting k = -20 in -14 = k + 6
-14 = -20 + 6
Question 16.
x + 4 = -14
Answer:
x = -18
Explanation:
Subtract 4 from both sides
x + 4 – 4 = -14 – 4
x = -18
Substituting x = -18 in x + 4 = -14
-18 + 4 = -14
Question 17.
g – 9 = -19
Answer:
g = -10
Explanation:
Add 9 to both sides.
g – 9 + 9 = -19 + 9
g = -10
Substituting g = -10 in g – 9 = -19
-10 – 9 = -19
Question 18.
c – 7.6 = -4
Answer:
c = 3.6
Explanation:
Add 7.6 to both sides
c – 7.6 + 7.6 = -4 + 7.6
c = 3.6
Substituting c = 3.6 in c – 7.6 = -4
3.6 – 7.6 = -4
Question 19.
-10.1 = w + 5.3
Answer:
w = -15.4
Explanation:
Subtract 5.3 from both sides
-10.1 – 5.3 = w + 5.3 – 5.3
-15.4 = w
Substituting w = -15.4 in -10.1 = w + 5.3
-10.1 = -15.4 + 5.3
Question 20.
![]()
Answer:
q = -1/6
Explanation:
Subtract 2/3 from both sides
1/2 – 2/3 = q + 2/3 – 2/3
(3 – 4)/6 = q
q = -1/6
Substituting q = -1/6 in 1/2 – 2/3 = q + 2/3 – 2/3
1/2 = -1/6 + 2/3
= (-1 + 4)/6 = 3/6 = 1/2
Question 21.
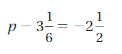
Answer:
p = 4/6
Explanation:
p – 19/6 = -5/2
Adding 19/6 to both sides
p – 19/6 + 19/6 = -5/2 + 19/6
p = (-15 + 19)/6
p = 4/6
Substituting p = 4/6 in p – 19/6 = -5/2
4/6 – 19/6 = -5/2
(-15/6) = -/2
Question 22.
-9.3 = d – 3.4
Answer:
d = -5.9
Explanation:
Add 3.4 to both sides
-9.3 + 3.4 = d – 3.4 + 3.4
d = -5.9
Substituting d = -5.9 in -9.3 = d – 3.4
-9.3 = -5.9 – 3.4
Question 23.
4.58 + y = 2.5
Answer:
y = -2.08
Explanation:
Subtract 4.58 from both sides
4.58 + y – 4.58 = 2.5 – 4.58
y = -2.08
Putting y = -2.08 in 4.58 + y = 2.5
4.58 – 2.08 = 2.5
Question 24.
x – 5.2 = -18.73
Answer:
x = -13.53
Explanation:
Add 5.2 to both sides
x – 5.2 + 5.2 = -18.73 + 5.2
x = -13.53
Putting x = -13.53 in x – 5.2 = -18.73
-13.53 – 5.2 = -18.73
Question 25.
![]()
Answer:
q = 10/9
Explanation:
Subtract 5/9 from both sides
q + 5/9 – 5/9 = 5/6 – 5/9
q = (15 – 5)/9 = 10/9
Substituting q = 10/9 in q + 5/9 = 5/6
10/9 + 5/9 = 15/9 = 5/6
Question 26.
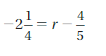
Answer:
r = -19/20
Explanation:
-7/4 = r – 4/5
Adding 4/5 to both sides
-7/4 + 4/5 = r – 4/5 + 4/5
(-35 + 16)/20 = r
r = -19/20
Putting r = -19/20 in -7/4 = r – 4/5
-7/4 = -19/20 – 4/5
= (-19 – 16)/20 = -35/20 = -7/4
Question 27.
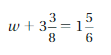
Answer:
w = -74/48
Explanation:
w + 27/8 = 11/6
Subtract 27/8 from both sides
w + 27/8 – 27/8 = 11/6 – 27/8
w = (88 – 162)/48
w = -74/48
Putting w = -74/48 in w + 27/8 = 11/6
-74/48 + 27/8
(-74 + 162)/48 = 88/48 = 11/6
Question 28.
YOU BE THE TEACHER
Your friend solves the equation x + 8 = 10. Is your friend correct? Explain your reasoning.
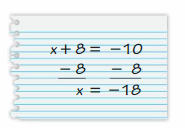
Answer:
My friend is not correct.
Explanation:
x + 8 = 10
x = 10 – 8
x = 2
The above mentioned is the correct solution. As my friend taken x + 8 = -10, there she did mistake.
WRITING AND SOLVING AN EQUATION
Write the word sentence as an equation. Then solve the equation.
Question 29.
4 less than a number n is -15.
Answer:
4 – n = -15
n = 19
Explanation:
As 4 is less than a number n subtract 4 from n.
4 – n = -15
Add n to sides of the equation
4 – n + n = -15 + n
4 = -15 + n
Add 15 to both sides
4 + 15 = -15 + n + 15
n = 19
Question 30.
10 more than a number c is 3.
Answer:
10 + c = 3
c = -7
Explanation:
As 10 is more than c add 10 to c
10 + c = 3
Subtract 10 from both sides
10 + c – 10 = 3 – 10
c = -7
Question 31.
The sum of a number y and -3 is -8.
Answer:
y – 3 = -8
y = -5
Explanation:
y + (-3) = -8
y – 3 = -8
y – 3 + 3 = -8 + 3
y = -5
Question 32.
The difference of a number p and 6 is 14.
Answer:
p – 6 = 14
p = 20
Explanation:
p – 6 = 14
p – 6 + 6 = 14 + 6
p = 20
Question 33.
MODELING REAL LIFE
The temperature of dry ice is -109.3°F. This is 184.9°F less than the outside temperature. Write and solve an equation to find the outside temperature.
Answer:
-109.3°F = x – 184.9°F
Outside temperature is -24.4°F.
Explanation:
The temperature of dry ice = -109.3°F
Let us take the outside temperature as x.
dry ice is 84.9°F less than the outside temperature
-109.3°F = x – 184.9°F
x = -109.3°F + 184.9°F
x = 75.6°F
Therefore, Outside temperature is -24.4°F
Question 34.
MODELING REAL LIFE
A company makes a profit of $1.38 million. This is $2.54 million more than last year. What was the profit last year? Justify your answer.
Answer:
The last year company got $1.16 millions loss.
Explanation:
A company makes a profit of $1.38 million
Let us take last year profit as p.
p + $2.54 = $1.38
p = $1.38 – $2.54
p = -$1.16
The last year company was at a loss of $1.16 million.
Question 35.
MODELING REAL LIFE
The difference in elevation of a helicopter and a submarine is 18\(\frac{1}{2}\) meters. The elevation of the submarine is -7\(\frac{3}{4}\) meters. What is the elevation of the helicopter? Justify your answer.
Answer:
The elevation of the helicopter is 49/4 meters.
Explanation:
Let us take the elevation of the helicopter as x.
The elevation of the submarine = -7(3/4) = -25/4
x – 18(1/2) = -25/4
x – 37/2 = -25/4
x = -25/4 + 37/2
x = (-25 + 74)/4 = 49/4
So, the elevation of the helicopter is 49/4
GEOMETRY
What is the unknown side length?
Question 36.
Perimeter = 12 cm
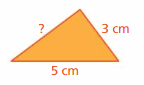
Answer:
The unknown side length is 4 cm.
Explanation:
Let us take the unknown side length as x cm.
Perimeter = 12 cm
x + 3 + 5 = 12
x + 8 = 12
x = 12 – 8
x = 4 cm
Question 37.
Perimeter = 24.2 in.
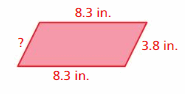
Answer:
The unknown side length is 3.8 in.
Explanation:
Let us take the unknown side length as x inches
Perimeter = 24.2 in.
x + 8.3 + 3.8 + 8.3 = 24.2
x + 20.4 = 24.2
x = 24.2 – 20.4
x = 3.8 in
Question 38.
Perimeter = 34.6 ft
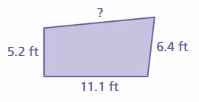
Answer:
The unknown side length is 11.9 ft
Explanation:
Let us take the unknown side length as x ft.
Perimeter = 34.6 ft
5.2 + 11.1 + 6.4 + x = 34.6
22.7 + x = 34.6
x = 34.6 – 22.7
x = 11.9 ft
Question 39.
MODELING REAL LIFE
The total height of the Statue of Liberty and its pedestal is 153 feet more than the height of the statue. What is the height of the statue? Justify your answer.

Answer:
The height of statue is 152 feet.
Explanation:
Let us take the height of the statue as x feet.
The total height of the Statue of Liberty and its pedestal = x + 153
305 = x + 153
x = 305 – 153
x = 152 feet
So, the height of statue is 152 feet.
Question 40.
PROBLEM SOLVING
When bungee jumping, you reach a positive elevation on your first jump that is 50\(\frac{1}{6}\) feet greater than the elevation you reach on your second jump. Your change in elevation on the first jump is -200\(\frac{2}{3}\)feet. What is your change in elevation on the second jump?
Answer:
The height of second jump is 301/2 feet.
Explanation:
The height of the first jump = 200(2/3) = 602/3
The height of second jump = The height of the first jump – 50(1/6)
= -602/3 – 301/6
= (1204 – 301)/6 = 903/6 = 301/2
The height of second jump is 301/2 feet.
Question 41.
MODELING REAL LIFE
Boatesville is a 65\(\frac{3}{5}\)-kilometer drive from Stanton. A bus traveling from Stanton to Boatesville is 24 \(\frac{1}{3}\) kilometers from Boatesville. How far has the bus traveled? Justify your answer.
Answer:
The bus travelled 619/5 km from Boatesville.
Explanation:
The distance between Boatesville and stanton = 65(3/5) = 328/5
The distance between Stanton and bus = 24(1/3) = 73/3
The bus travelled = 328/5 – 73/3 = (984 – 365)/15
= 619/15
Question 42.
GEOMETRY
The sum of the measures of the angles of a triangle equals 180°. What is the missing angle measure?
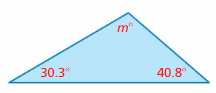
Answer:
Missing angle is 108.9°.
Explanation:
The sum of the measures of the angles of a triangle equals 180°
30.3 + m + 40.8 = 180
71.1 + m = 180
m = 180 – 71.1 = 108.9°
Question 43.
DIG DEEPER!
The table shows your scores in a skateboarding competition. The first-place finisher scores 311.62 total points, which is 4.72 more points than you score. What is your score in the fourth round?
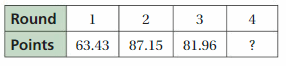
Answer:
Your score in the fourth round is 74.36 points.
Explanation:
The first-place finisher scores 311.62 total points, which is 4.72 more points than you score
63.43 + 87.15 + 81.96 + x + 4.72 = 311.62
x + 237.26 = 311.62
x = 311.62 – 237.26
x = 74.36
Question 44.
CRITICAL THINKING
Find the value of 2x – 1 when x + 6 = -2.
Answer:
2x – 1 = -17
Explanation:
x + 6 = -2
x = -2 – 6
x = -8
putting x = -8 in 2x – 1
2(-8) – 1 = -16 – 1 = -17
CRITICAL THINKING
Solve the equation.
Question 45.
| x | = 2
Answer:
x = ± 2
Explanation:
When mod x is 2, then x is plus or minus 2.
Question 46.
| x | – 2 = -2
Answer:
x = 0
Explanation:
| x | = -2 + 2
| x | = 0
Question 47.
| x | + 5 = 18
Answer:
x = ± 13
Explanation:
| x | = 18 – 5
| x | = 13
x = ± 13
Lesson 4.2 Solving Equations Using Multiplication or Division
EXPLORATION 1
Using Algebra Tiles to Solve Equations
Work with a partner.
a. Use the examples to explain the meaning of each property.
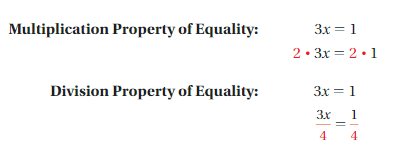
Are these properties true for equations involving negative numbers? Explain your reasoning.
b. Write the three equations modeled by the algebra tiles. Explain how you can use algebra tiles to solve each equation. Then find the solutions.
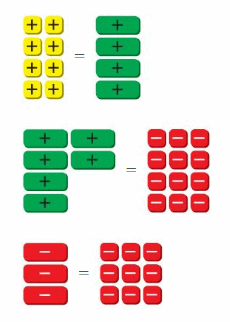

c. How can you solve each equation in part(b) without using algebra tiles?
4.2 Lesson
Try It
Solve the equation. Check your solution.
Question 1.
\(\frac{x}{5}\) = -2
Answer:
x = -10
Explanation:
x/5 = -2
x = -2 x 5
x = -10
Putting x = -10 in x/5 = -2
-10/5 = -2
Question 2.
-a = -24
Answer:
a = 24
Explanation:
a = 24
Question 3.
3 = -1.5n
Answer:
n = -2
Explanation:
n = -3/1.5
n = -2
Try It
Solve the equation. Check your solution.
Question 4.
–\(\frac{8}{5}\)b = 5
Answer:
b = -25/8
Explanation:
-8/5 b = 5
-b = 5 x (5/8)
-b = 25/8
b = -25/8
Substituting b = -25/8 in -8/5 b = 5
-8/5 (-25/8) = (25 x 8)/(8 x 5) = 5
Question 5.
\(\frac{3}{8}\)h = -9
Answer:
h = -24
Explanation:
3/8 h = -9
h = -9 x (8/3)
h = -3 x 8 = -24
Substituting h = -24 in 3/8 h = -9
3/8 (-24) = 3 x -3 = -9
Question 6.
-14 = \(\frac{2}{3}\)x
Answer:
x = -21
Explanation:
-14 = (2/3) x
x = -14 x (3/2)
x = -7 x 3 = -21
Substituting x = -21 in -14 = (2/3) x
-14 = (2/3) -21 = 2 x -7
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
SOLVING AN EQUATION
Solve the equation. Check your solution.
Question 7.
6d = 24
Answer:
d = 4
Explanation:
6d = 24
d = 24/6
d = 4
Putting d = 4 in 6d = 24
6 x 4 = 24
Question 8.
\(\frac{t}{3}\) = -4
Answer:
t = -12
Explanation:
t/3 = -4
t = -4 x 3
t = -12
Putting t = -12 in t/3 = -4
-12/3 = -4
Question 9.
–\(\frac{2}{5}\)p = -6
Answer:
p = 15
Explanation:
(-2/5) p = -6
p = -6 x (-5/2)
p = 3 x 5 = 15
Putting p = 15 in (-2/5) p = -6
(-2/5) 15 = -2 x 3 = -6
Question 10.
WRITING
Explain why you can use multiplication to solve equations involving division.
Answer:
Multiplication is the inverse of division. So it can easily undo the operation.
Question 11.
WRITING
Are the equations \(\frac{2}{3}\)m = -4 and -4m = 24 equivalent? Explain.
Answer:
Both the given equations are equivalent.
Explanation:
(2/3)m = -4 and -4m = 24
m = -4 x (3/2) and m = -24/4
m = -2 x 3 and m = -6
m = -6 and m = -6
Yes both the equations are equivalent.
Question 11.
REASONING
Describe the inverse operation that will undo the given operation.
Answer:
The inverse operation of division is the multiplication and they are opposite. When dividing a number by a, the multiplication by a will undo the operation.
Question 12.
subtracting 12
Answer:
Adding 12.
Explanation:
The inverse operation of subtraction is addition.
Question 13.
multiplying by –\(\frac{1}{8}\)
Answer:
Dividing by (-8)
Explanation:
The inverse operation of multiplication is division. So, dividing by (-8)
Question 14.
adding -6
Answer:
Subtracting -6
Explanation:
The inverse operation for addition is subtraction. So, subtracting -6.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 15.
The elevation of the surface of a lake is 315 feet. During a drought, the water level of the lake changes -3\(\frac{1}{5}\) feet per week. Find how long it takes for the surface of the lake to reach an elevation of 299 feet. Justify your answer.
Answer:
It takes 5 weeks for the surface of the lake to reach an elevation of 299 feet
Explanation:
Let us take the number of weeks as x.
The lake reduced = 315 – 299 = 16 feet
-3(1/5)x = 16
-16/5 x = 16
x = -16 (5/16)
x = 5
It takes 5 weeks for the surface of the lake to reach an elevation of 299 feet
Question 16.
DIG DEEPER!
The patio shown has an area of 116 square feet. What is the value of h? Justify your answer.
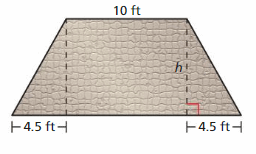
Answer:
h = 8
Explanation:
Total area = 116
Triangle 1 + rectangle + triangle2 = 116
1/2 x 4.5 x h + 10 x h + 1/2 x 4.5 x h = 116
10h + 4.5h = 116
14.5h = 116
h = 116/14.5 = 8
Solving Equations Using Multiplication or Division Homework & Practice 4.2
Review & Refresh
Solve the equation. Check your solution.
Question 1.
n – 9 = -12
Answer:
n = -3
Explanation:
n = -12 + 9
n = -3
Putting n = -3 in n – 9 = -12
-3 – 9 = -12
Question 2.
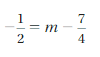
Answer:
m = 5/4
Explanation:
-1/2 = m – (7/4)
m = -1/2 + 7/4
m = (-2 + 7)/4 = 5/4
Putting m = 5/4 in -1/2 = m – (7/4)
-1/2 = 5/4 – (7/4) = (5 – 7)/4
= -2/4 = -1/2
Question 3.
-6.4h = h + 8.7
Answer:
h = -1.75
Explanation:
-6.4h = h + 8.7
h + 6.4h = -8.7
7.4h = -8.7
h = -8.7/7.4
h = -1.75
Putting h = -1.175 in -6.4h = h + 8.7
-6.4 x -1.175 = -1.175 + 8.7
7.52 = 7.52
Find the difference.
Question 4.
5 – 12
Answer:
-7
Explanation:
5 – 12 = -7
Question 5.
-7 – 2
Answer:
-9
Explanation:
-7 – 2 = -9
Question 6.
4 – (-8)
Answer:
12
Explanation:
4 – (-8) = 4 + 8 = 12
Question 7.
-14 – (-5)
Answer:
-9
Explanation:
-14 – (-5) = -14 + 5 = -9
Question 8.
Of the 120 apartments in a building, 75 have been scheduled to receive new carpet. What percent of the apartments have not been scheduled to receive new carpet?
A. 25%
B. 37.5%
C. 62.5%
D. 75%
Answer:
B
Explanation:
Total number of apartments = 120
The number of apartments has not been scheduled to receive new carpet = 120 – 75 = 45
Percentage = (45/120) x 100 = 37.5%
Concepts, Skills, &Problem Solving
USING ALGEBRA TILES
Solve the equation using algebra tiles. Explain your reasoning. (See Exploration 1, p. 133.)
Question 9.
4x = -16
Answer:
x = -4
Explanation:
4x = -16
x = -16/4 = -4
Question 10.
2x = -6
Answer:
x = -3
Explanation:
2x = -6
x = -6/2 = -3
Question 11.
-5x = -20
Answer:
x = 4
Explanation:
-5x = -20
5x = 20
x = 20/5 = 4
SOLVING AN EQUATION
Solve the equation. Check your solution.
Question 12.
4x = -16
Answer:
x = -4
Explanation:
4x = -16
x = -16/4 = -4
Putting x = -4 in 4x = -16
4(-4) = -16
Question 13.
2x = -6
Answer:
x = -3
Explanation:
2x = -6
x = -6/2 = -3
Putting x = -3 in 2x = -6
2(-3) = -6
Question 14.
\(\frac{n}{2}\) = -7
Answer:
n = -14
Explanation:
n/2 = -7
n = -7 x 2 = -14
Putting n = -14 in n/2 = -7
-14/2 = -7
Question 15.
\(\frac{k}{-3}\) = 9
Answer:
k = -27
Explanation:
k/-3 = 9
k = 9 x -3 = -27
Putting k = -27 in k/-3 = 9
-27/-3 = 9
Question 16.
5m = -10
Answer:
m = -2
Explanation:
m = -10/5
m = -2
Putting m = -2 in 5m = -10
5(-2) = -10
Question 17.
8t = -32
Answer:
t = -4
Explanation:
t = -32/8 = -4
Putting t = -4 in 8t = -32
8(-4) = -32
Question 18.
-0.2x = 1.6
Answer:
x = -8
Explanation:
-0.2x = 1.6
x = -1.6/0.2
x = -8
Putting x = -8 in -0.2x = 1.6
-0.2 (-8) = 1.6
Question 19.
-10 = –\(\frac{b}{4}\)
Answer:
b = 40
Explanation:
-10 = -(b/4)
b/4 = 10
b = 10 x 4 = 40
Putting b = 40 in -10 = -(b/4)
-10 = -(40/4) = -10
Question 20.
-6p = 48
Answer:
p = -8
Explanation:
-6p = 48
p = -48/6 = -8
Putting p = -8 in -6p = 48
-6(-8) = 48
Question 21.
-72 = 8d
Answer:
d = -9
Explanation:
-72 = 8d
d = -72/8
d = -9
Putting d = -9 in -72 = 8d
-72 = 8 (-9)
Question 22.
\(\frac{n}{1.6}\) = 5
Answer:
n = 8
Explanation:
n/1.6 = 5
n = 1.6 x 5
n = 8
Putting n = 8 in n/1.6 = 5
8/1.6 = 80/16 = 5
Question 23.
-14.4 = -0.6p
Answer:
p = 24
Explanation:
-14.4 = -0.6p
0.6p = 14.4
p = 14.4/0.6
p = 144/6 = 24
Putting p = 24 in -14.4 = -0.6p
-14.4 = -0.6 x 24
Question 24.
\(\frac{3}{4}\)g = -12
Answer:
g = -16
Explanation:
(3/4)g = -12
3g = -12 x 4
3g = -48
g = -48/3
g = -16
Putting g = -16 in (3/4)g = -12
(3/4) x (-16) = 3 x -4 = -12
Question 25.
8 = –\(\frac{2}{5}\)c
Answer:
c = -20
Explanation:
8 = -(2/5)c
-2c = 8 x 5 = 40
2c = -40
c = -40/2 = -20
Putting c = -20 in 8 = -(2/5)c
8 = -(2/5) x -20 = (2/5)20 = 2 x 4
= 8
Question 26.
–\(\frac{4}{9}\)f = -3
Answer:
f = 27/4
Explanation:
-(4/9)f = -3
(4/9)f = 3
4f = 3 x 9 = 27
f = 27/4
Putting f = 27/4 in -(4/9)f = -3
-(4/9) x (27/4) = -27/9 = -3
Question 27.
26 = –\(\frac{8}{5}\)y
Answer:
y = -130/8
Explanation:
26 = -(8/5)y
-8y = 26 x 5 = 130
y = -130/8
Putting y = -65/4 in 26 = -(8/5)y
26 = -(8/5) x (-130/8) = 130/5 = 26
Question 28.
YOU BE THE TEACHER
Your friend solves the equation -4.2x = 21. Is your friend correct? Explain your reasoning.
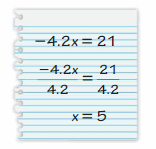
Answer:
My friend is wrong.
Explanation:
-4.2x = 21
-x = 21/4.1
x = -5.12
WRITING AND SOLVING AN EQUATION
Write the word sentence as an equation. Then solve the equation.
Question 29.
A number multiplied by -9 is -16.
Answer:
9n = 16
n = 16/9
Explanation:
n x -9 = -16
9n = 16
n = 16/9
Question 30.
A number multiplied by \(\frac{2}{5}\) is \(\frac{3}{20}\).
Answer:
(2/5)n = 3/20
n = 15/40
Explanation:
n x (2/5) = 3/20
(2/5)n = 3/20
n = (3/20) x (5/2)
= 15/40
Question 31.
The product of 15 and a number is -75.
Answer:
15n = -75
n = -5
Explanation:
15 x n = -75
15n = -75
n = -75/15
n = -5
Question 32.
The quotient of a number and -1.5 is 21.
Answer:
n/-1.5 = 21
n = -31.5
Explanation:
n/-1.5 = 21
-n/1.5 = 21
-n = 21 x 1.5
-n = 31.5
n = -31.5
Question 33.
MODELING REAL LIFE
You make a profit of $0.75 for every bracelet you sell. Write and solve an equation to determine how many bracelets you must sell to earn enough money to buy the soccer cleats shown.
Answer:
I need to sell 48 bracelets to earn enough money to buy the soccer cleats shown.
Explanation:
Let us take a number of bracelets as x.
0.75x = 36
x = 36/0.75
x = 48
Question 34.
MODELING REAL LIFE
A rock climber averages 12\(\frac{3}{5}\) feet climbed per minute. How many feet does the rock climber climb in 30 minutes? Justify your answer.
Answer:
Climber climbs 378 feet in 30 minutes.
Explanation:
A rock climber averages 63/5 feet climbed per minute
Let us take he climb x feet in 30 minutes
x/30 = 63/5
x = (63/5) x 30
x = 63 x 6
x = 378 feet
OPEN-ENDED
Write (a) a multiplication equation and (b) a division equation that has the given solution.
Question 35.
-3
Answer:
(a) 3x = -9
(b) x/3 = -1
Explanation:
(a) 3x = -9
x = -9/3 = -3
x/3 = -1
x = -1 x 3 = -3
Question 36.
-2.2
Answer:
(a) -5x = 11
(b) x/2 = -1.1
Explanation:
(a) -5x = 11
x = -11/5
x = -2.2
(b) x/2 = -1.1
x = 2 x -1.1
x = -2.2
Question 37.
–\(\frac{1}{2}\)
Answer:
(a) 6x = -3
(b) -x/4 = 0.125
Explanation:
(a) 6x = -3
x = -3/6 = -1/2
(b) -x/4 = 0.125
-x = 0.125 x 4 = 0.5
x = -0.5
Question 38.
-1\(\frac{1}{4}\)
Answer:
(a) 4x = 5
(b) x/2 = 10/16
Explanation:
(a) 4x = 5
x = 5/4 = 1(1/4)
(b) x/2 = 10/16
x = 2(10/16)
x = 10/8 = 5/4
Question 39.
REASONING
Which method(s) can you use to solve –\(\frac{2}{3}\)c = 16?

Answer:
Multiply each side by -3/2.
Explanation:
-(2/3)c = 16
Multiply both sides by -(3/2)
-(2/3)c x (-3/2) = 16 x (-3/2)
c = -8 x 3 = -24
Question 40.
MODELING REAL LIFE
A stock has a return of -$1.26 per day. Find the number of days until the total return is -$10.08. Justify your answer.
Answer:
The number of days required is 8 days.
Explanation:
Let us take the number of days as x.
Multiply number of days by one day return to get a total return
-$1.26 * x = -$10.08
x = 10.08/1.26
x = 8
Question 41.
PROBLEM-SOLVING
In a school election, \(\frac{3}{4}\) of the students vote. There are 1464 votes. Find the number of students. Justify your answer.
Answer:
The number of students who voted is 1098 and the number of students who not voted is 366.
Explanation:
The number of students voted = (3/4) x 1464
= 366 x 3 = 1098
So, 75% of students are 1098
Remaining 25% = 1098 x (25/75)
= 1098 x (1/3) = 366
The number of students voted is 1098 and number of students not voted is 366.
Question 42.
DIG DEEPER!
The diagram shows Aquarius, an underwater ocean laboratory located in the Florida Keys National Marine Sanctuary. The equation \(\frac{31}{25}\)x = -62 can be used to calculate the depth of Aquarius. Interpret the equation. Then find the depth of Aquarius. Justify your answer.

Answer:
The depth of the aquarius is -50 feet
Explanation:
(31/25)x = -62
Multiply both sides by (25/31)
(31/25)x . (25/31) = -62 . (25/31)
x = (-2) x 25
x = -50
The depth of the aquarius is -50 feet
Question 43
DIG DEEPER!
The price of a bike at Store A is \(\frac{5}{6}\) the price at Store B. The price at Store A is $150.60. Find how much you save by buying the bike at Store A. Justify your answer.
Answer:
The amount saved is $30.12
Explanation:
Let us take the price of the bike at store b as x.
$150.60 = (5/6)x
150.6 * (6/5) = x
x = 30.12 * 6 = 180.72
The amount saved is $180.72 – $150.60 = $30.12
Question 44.
CRITICAL THINKING
Solve -2| m | = -10.
Answer:
m = 5
Explanation:
-2m = -10
2m = 10
m = 10/2 = 5
Question 45.
NUMBER SENSE
In 4 days, your family drives \(\frac{5}{7}\) of the total distance of a trip. The total distance is 1250 miles. At this rate, how many more days will it take to reach your destination? Justify your answer.
Answer:
It took 1(1/2) day to reach the destination.
Explanation:
The distance travelled in 4 days = 1250 * (5/7)
= 892.857 miles
The distance travelled in 1 day = 892.857/4 = 223.214
Remaining distance = 1250 – 892.57 = 357.14
357.14 = 223.214x
x = 357.14/223.214 = 1.59
So, it took 1(1/2) day to reach the destination.
Lesson 4.3 Solving Two-Step Equations
EXPLORATION 1
Using Algebra Tiles to Solve Equations
Work with a partner.
a. What is being modeled by the algebra tiles below? What is the solution?
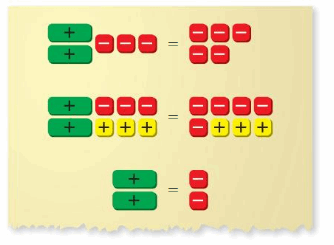
b. Use properties of equality to solve the original equation in part(a). How do your steps compare to the steps performed with algebra tiles?
c. Write the three equations modeled by the algebra tiles below. Then solve each equation using algebra tiles. Check your answers using properties of equality.
d. Explain how to solve an equation of the form ax + b = c for x.
4.3 Lesson
Try It
Solve the equation. Check your solution.
Question 1.
2x + 12 = 4
Answer:
x = -4
Explanation:
2x = 4 – 12 = -8
x = -8/2
x = -4
Putting x = -4 in 2x + 12 = 4
2(-4) + 12 = -8 + 12 = 4
Question 2.
-5c + 9 = -16
Answer:
c = 5
Explanation:
9 + 16 = 5c
5c = 25
c = 25/5
c = 5
Putting c = 5 in -5c + 9 = -16
-5(5) + 9 = -25 + 9 = -16
Question 3.
9 = 3x – 12
Answer:
x = 7
Explanation:
3x = 9 + 12
3x = 21
x = 21/3 = 7
Putting x = 7 in 9 = 3x – 12
9 = 3(7) – 12 = 21 – 12 = 9
4.3 Lesson
Try It
Solve the equation. Check your solution.
Question 4.
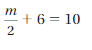
Answer:
m = 8
Explanation:
m/2 = 10 – 6
m/2 = 4
m = 2 x 4
m = 8
putting m = 8 in m/2 + 6 = 10
8/2 + 6 = 4 + 6 = 10
Question 5.
![]()
Answer:
z = -12
Explanation:
5 – 9 = z/3
z/3 = -4
z = -4 x 3
z = -12
Putting z = -12 in -z/3 + 5 = 9
-(-12)/3 + 5 = 12/3 + 5 = 4 + 5 = 9
Question 6.
![]()
Answer:
a = -2/5
Explanation:
2/5 + 4a =-6/5
4a = -6/5 – 2/5
4a = -8/5
a = (-8/5) x (1/4)
a = -2/5
Putting a = -2/5 in 2/5 + 4a =-6/5
2/5 + 4(-2/5) = 2/5 – 8/5 = (2 – 8)/5 = -6/5
Try It
Solve the equation. Check your solution.
Question 7.
4 – 2y + 3 = -9
Answer:
y = 8
Explanation:
7 – 2y = -9
7 + 9 = 2y
16 = 2y
y = 16/2
y = 8
Puuting y = 8 in 4 – 2y + 3 = -9
4 – 2(8) + 3 = 7 – 16 = -9
Question 8.
7x – 10x = 15
Answer:
x = -5
Explanation:
-3x = 15
x = -15/3
x = -5
Putting x = -5 in 7x – 10x = 15
7(-5) – 10(-5) = -35 + 50 = 15
Question 9.
-8 = 1.3m – 2.1m
Answer:
m = 10
Explanation:
-8 = -0.8m
m = 8/0.8
m = 10
Putting m = 10 in -8 = 1.3m – 2.1m
-8 = 1.3(10) – 2.1(10)
= 13 – 21
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
MATCHING
Match the equation with the step(s) to solve it.
Question 10.
4 + 4n = 12
Answer:
n = 2
Explanation:
4n = 12 – 4
4n = 8
n = 8/4
n = 2
Question 11.
4n = 12
Answer:
n = 3
Explanation:
n = 12/4
n = 3
Question 12.
\(\frac{n}{4}\) = 12
Answer:
n = 48
Explanation:
n/4 = 12
n = 12 x 4
n = 48
Question 13.
\(\frac{n}{4}\) – 4 = 12
A. Add 4 to each side. Then multiply each side by 4.
B. Subtract 4 from each side. Then divide each side by 4.
C. Multiply each side by 4.
D. Divide each side by 4.
Answer:
Add 4 to each side. Then multiply each side by 4.
Explanation:
n/4 – 4 = 12
Add 4 to each side
n/4 – 4 + 4 = 12 + 4
n/4 = 16
Multiply each side by 4
n/4 x 4 = 16 x 4
n = 64
SOLVING AN EQUATION
Solve the equation. Check your solution.
Question 14.
4p + 5 = 3
Answer:
p = -1/2
Explanation:
4p = 3 – 5
4p = -2
p = -2/4
p = -1/2
putting p = -1/2 in 4p + 5 = 3
4(-1/2) + 5 = -2 + 5 = 3
Question 15.
–\(\frac{d}{5}\) – 1 = -6
Answer:
d = 25
Explanation:
-1 + 6 = d/5
5 = d/5
d = 5 x 5
d = 25
Putting d = 25 in -d/5 – 1 = -6
-25/5 – 1 = -5 – 1 = -6
Question 16.
3.6g = 21.6
Answer:
g = 6
Explanation:
g = 21.6 / 6.3
g = 6
Putting g = 6 in 3.6g = 21.6
3.6(6) = 21.6
Question 17.
WRITING
Are the equations 3x + 12 = 6 and -2 = 4 – 3x equivalent? Explain.
Answer:
Equations are not equivalent
Explanation:
3x + 12 = 6 and -2 = 4 – 3x
3x = 6 – 12 and 3x = 4 + 2
3x = -6 and 3x = 6
x = -6/3 and x = 6/3
x = -2 and x = 2
Equations are not equivalent
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 18.
You must scuba dive to the entrance of your room at Jules’ Undersea Lodge in Key Largo, Florida. The diver is 1 foot deeper than \(\frac{2}{3}\) of the elevation of the entrance. What is the elevation of the entrance?
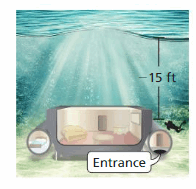
Answer:
The elevation of entrance is 21 feet
Explanation:
2/3 rd of elevation = -15 foot + 1 feet
(2/3) * x = 14
x = 14 * (3/2)
x = 7 * 3 = 21 foot
Question 19.
DIG DEEPER!
A car drives east along a road at a constant speed of 46 miles per hour. At 4:00 P.M., a truck is 264 miles away, driving west along the same road at a constant speed. The vehicles pass each other at 7:00 P.M. What is the speed of the truck?
Answer:
The speed of truck is 42 miles per hour
Explanation:
Speed = distance/time
The time taken is 3 hours
46 + x = 264/3
46 + x = 88
x = 88 – 46 = 42
Solving Two-Step Equations Homework & Practice 4.3
Review & Refresh
Solve the equation.
Question 1.
3z = 18
Answer:
z = 6
Explanation:
z = 18/3
z = 6
Question 2.
-8p = 40
Answer:
p = -5
Explanation:
-p = 40/8
-p = 5
p = -5
Question 3.
–\(\frac{m}{4}\) = 5
Answer:
m = -20
Explanation:
-m/4 = 5
-m = 5 x 4
-m = 20
m = -20
Question 4.
\(\frac{5}{6}\)k = -10
Answer:
k = -12
Explanation:
(5/6)k = -10
k = -10(6/5)
k = -2(6)
k = -12
Multiply or divide.
Question 5.
-6.2 × 5.6
Answer:
-6.2 × 5.6 = -34.72
Explanation:
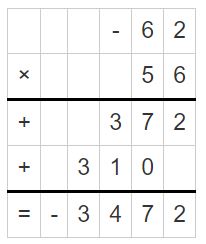
Question 6.
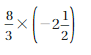
Answer:
-40/6
Explanation:
(8/3) x (-5/2) = -40/6
Question 7.
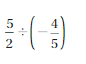
Answer:
-25/8
Explanation:
(5/2) / (-4/5) = (5 x 5) / (2 x – 4)
= -25/8
Question 8.
-18.6 ÷ (-3)
Answer:
6.2
Explanation:
-18.6 ÷ (-3) = 186/30
= 6.2
Question 9.
Which fraction is not equivalent to 0.75?

Answer:
6/9 is not equivalent to 0.75
Explanation:
15/20 = 3/4 = 0.75
9/12 = 3/4 = 0.75
6/9 = 2/3 = 0.66
Concepts, Skills, & Problem Solving
USING ALGEBRA TILES
Write the equation modeled by the algebra tiles. Then solve the equation using algebra tiles. Check your answer using properties of equality. (See Exploration 1, p. 139.)
Question 10.

Question 11.
SOLVING AN EQUATION
Solve the equation. Check your solution.
Question 12.
2v + 7 = 3
Answer:
v = -2
Explanation:
2v = 3 – 7
2v = -4
v = -4/2
v = -2
Putting v = -2 in 2v + 7 = 3
2(-2) + 7 = -4 + 7 = 3
Question 13.
4b + 3 = -9
Answer:
b = -3
Explanation:
4b = -9 – 3
4b = -12
b = -12/4
b = -3
Putting b = -3 in 4b + 3 = -9
4(-3) + 3 = -12 + 3 = -9
Question 14.
17 = 5k – 2
Answer:
k = 19/5
Explanation:
5k = 17 + 2
5k = 19
k = 19/5
Putting k = 19/5 in 5k = 17 + 2
5(19/5) – 2 = 19 – 2 = 17
Question 15.
-6t – 7 = 17
Answer:
t = -4
Explanation:
-6t = 17 + 7
-6t = 24
t = -24/6
t = -4
Putting t = -4 in -6t – 7 = 17
-6(-4) – 7 = 24 – 7 = 17
Question 16.
8n + 16.2 = 1.6
Answer:
n = -1.825
Explanation:
8n = 1.6 – 16.2
8n = -14.6
n = -14.6/8
n = -1.825
Putting n = -1.825 in 8n + 16.2 = 1.6
8(-1.825) + 16.2 = -14.6 + 16.2 = 1.6
Question 17.
-5g + 2.3 = -18.8
Answer:
g = 4.22
Explanation:
2.3 + 18.8 = 5g
5g = 21.1
g = 21.1/5
g = 4.22
putting g = 4.22 in -5g + 2.3 = -18.8
-5(4.22) + 2.3 = -21.1 + 2.3 = -18.8
Question 18.
2t + 8 = -10
Answer:
t = -9
Explanation:
2t = -10 – 8
2t = -18
t = -18/2
t = -9
Putting t = -9 in 2t + 8 = -10
2(-9) + 8 = -18 + 8 = -10
Question 19.
-4p + 9 = -5
Answer:
p = 3.5
Explanation:
4p = 9 + 5
4p = 14
p = 14/4
p = 3.5
Putting p = 3.5 in -4p + 9 = -5
-4(3.5) + 9 = -14 + 9 = -5
Question 20.
15 = -5x + 10
Answer:
x = -1
Explanation:
15 – 10 = -5x
-5x = 5
x = -5/5
x = -1
Putting x = -1 in 15 = -5x + 10
15 = -5(-1) + 10 = 5 + 10
= 15
Question 21.
10.35 + 2.3h = -9.2
Answer:
h = -8.5
Explanation:
2.3h = -9.2 – 10.35
2.3h = -19.55
h = -19.55/2.3
h = -8.5
Putting h = -8.5 in 10.35 + 2.3h = -9.2
10.35 + 2.3(-8.5) = 10.35 – 19.55 = -9.2
Question 22.
-4.8f + 6.4 = -8.48
Answer:
f = 3.1
Explanation:
-4.8f = -8.48 – 6.4
-4.8f = -14.88
4.8f = 14.88
f = 14.88/4.8
f = 3.1
Putting f = 3.1 in -4.8f + 6.4 = -8.48
-4.8(3.1) + 6.4 = -14.88 + 6.4 = -8.48
Question 23.
7.3y – 5.18 = -51.9
Answer:
y = -6.4
Explanation:
7.3y = -51.9 + 5.18
7.3y = -46.72
y = -46.72/7.3
y = -6.4
Putting y = -6.4 in 7.3y – 5.18 = -51.9
7.3(-6.4) – 5.18 = -46.72 – 5.18 = -51.9
YOU BE THE TEACHER
Your friend solves the equation. Is your friend correct? Explain your reasoning.
Question 24.
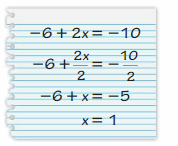
Answer:
My friend is wrong.
Explanation:
-6x + 2x = -10
-4x = -10
x = 10/4
x = 5/2
Question 25.
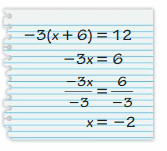
Answer:
My friend is wrong.
Explanation:
-3(x + 6) = 12
x + 6 = -12/3
x + 6 = -4
x = -4 – 6
x = -10
SOLVING AN EQUATION
Solve the equation. Check your solution.
Question 26.

Answer:
g = -5
Explanation:
(3/5)g = -10/3 + 1/3
(3/5)g = (-10 + 1)/3
= -9/3 = -3
(3/5)g = -3
g = -3 x (5/3)
g = -5
Putting g = -5 in (3/5)g -1/3 = -10/3
(3/5)(-5) -1/3 = -3 – 1/3 = (-9 – 1)/3
= -10/3
Question 27.
![]()
Answer:
a = 4/3
Explanation:
a/4 = -1/2 + 5/6
a/4 = (-3 + 5)/6
a/4 = 2/6
a = (2/6) x 4
a = 4/3 = 1.33
Putting a = 4/3 in a/4 – 5/6 = -1/2
(1.33)/4 – 5/6 = (4 – 10)/12 = -6/12 = -1/2
Question 28.
![]()
Answer:
z = -3/2
Explanation:
(4 + z) = -5/6 x -3
4 + z = 5/2
z = 5/2 – 4
z = (5 – 8)/2
z = -3/2
putting z = -3/2 in -1/3(4 + z) = -5/6
-1/3(4 + (-3/2)) = -1/3(4 – 3/2)
= -1/3(8-3)/2 = -1/6 x (5)
= -5/6
Question 29.
![]()
Answer:
b = 27/2
Explanation:
2 + 5/2 = b/3
(4 + 5)/2 = b/3
b/3 = 9/2
b = 9/2 x 3
b = 27/2
Putting b = 27/2 in 2 – b/3 = – 5/2
2 – (27/2)/3 = 2 – 27/6
= (12 – 27)/6 = -15/6 = – 5/2
Question 30.
![]()
Answer:
x = -27/20
Explanation:
(x + 3/5) = 1/2 x (-3/2)
x + 3/5 = -3/4
x = -3/4 – 3/5
x = (-15 – 12)/20
x = -27/20
Putting x = -27/20 in -2/3(x + 3/5) = 1/2
-2/3(-27/20 + 3/5) = -2/3(-27 + 12)/20
= -2/3(-15/20) = (2 x 15)/(3 x 20)
= 30/60 = 1/2
Question 31.
![]()
Answer:
v = -1/30
Explanation:
-9/4 v = 7/8 – 4/5
-9/4 v = (35 – 32)/40 = 3/40
v = -3/40 x 4/9
v = -1/30
Putting v = -1/30 in -9/4 v + 4/5 = 7/8
-9/4 v + 4/5 = -9/4 (-1/30) + 4/5
= 3/40 + 4/5 = (3 + 32)/40
= 35/40 = 7/8
Question 32.
PRECISION
Starting at 1:00 P.M., the temperature changes -4°F per hour. Write and solve an equation to determine how long it will take for the temperature to reach -1°F.

Answer:
Iit takes 8 hours 30 minutes.
Explanation:
Starting at 1:00 P.M., the temperature changes -4°F per hour.
The temperature change is 35 – 1 = 34°F
So, the equation is 4x = 34
x = 34/4
x = 8.5
S,o, it takes 8 hours 30 minutes.
COMBINING LIKE TERMS
Solve the equation. Check your solution.
Question 33.
3v – 9v = 30
Answer:
v = -5
Explanation:
-6v = 30
v = -30/6
v = -5
Putting v = -5 in 3v – 9v = 30
3(-5) – 9(-5) = -15 + 45 = 30
Question 34.
12t – 8t = -52
Answer:
t = -13
Explanation:
4t = -52
t = -52/4
t = -13
Putting t = -13 in 12t – 8t = -52
12(-13) – 8(-13) = -156 + 104 = -52
Question 35.
-8d – 5d + 7d = 72
Answer:
d = -12
Explanation:
-13d + 7d = 72
-6d = 72
d = -72/6
d = -12
Putting d = -12 in -8d – 5d + 7d = 72
-8(-12) – 5(-12) + 7(-12) = 96 + 60 – 84
= 156 – 84 = 72
Question 36.
-3.8g + 5 + 2.7g = 12.7
Answer:
g = -7
Explanation:
-1.1g + 5 = 12.7
-1.1g = 12.7-5
-1.1g = 7.7
g = -7.7/1.1
g = -7
Putting g = -7 in -3.8g + 5 + 2.7g = 12.7
-3.8(-7) + 5 + 2.7(-7) = 26.6 + 5 – 18.9 = 12.7
Question 37.
MODELING REAL LIFE
You have $9.25. How many games can you bowl if you rent bowling shoes? Justify your answer.

Answer:
3 games can be played
Explanation:
The amount you have is $9.25
After renting $9.25 – $2.50 = $6.75
Bowling per game = $2.25
After one game,
$2.25 gone out of $6.75
After two games,
$4.50 gone
After three games,
$6.75 gone
Total is $6.75, after three games it will cost you $6.75
So, 3 games can be played
Question 38.
MODELING REAL LIFE
A cell phone company charges a monthly fee plus $0.25 for each text message you send. The monthly fee is $30.00. You owe $59.50. How many text messages did you send? Justify your answer.
Answer:
You have sent 118 text messages.
Explanation:
Since the total cost of $59.50 is comprised of the monthly fee of $30 plus $0.25 for each text message, we can write
$59.50 = $30 + $0.25x
$0.25x = $59.50 – $30
$29.50 = $0.25x
x = 29.5/0.25
x = 118
So, you have sent 118 text messages
Question 39.
PROBLEM SOLVING
The height at the top of a roller coaster hill is 10 times the height h of the starting point. The height decreases 100 feet from the top to the bottom of the hill. The height at the bottom of the hill is -10 feet. Find h.
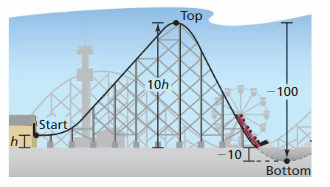
Answer:
h = -9
Explanation:
From the image, we can write the equation as,
-10 + 10h = -100
10h = -100 + 10
10h = -90
h = -90/10
h = -9
Question 40.
MODELING REAL LIFE
On a given day, the coldest surface temperature on the Moon, -280°F, is 53.6°F colder than twice the coldest surface temperature on Earth. What is the coldest surface temperature on Earth that day? Justify your answer.
Answer:
The coldest surface temperature on Earth is 166.8°F
Explanation:
the coldest surface temperature on the Moon = -280°F
2E + 53.6 = -280
2E = -280 – 53.6
2E = 333.6
E = 166.8°F
The coldest surface temperature on Earth is 166.8°F
Question 41.
DIG DEEPER!
On Saturday, you catch insects for your science class. Five of the insects escape. The remaining insects are divided into three groups to share in class. Each group has nine insects.
a. Write and solve an equation to find the number of insects you catch on Saturday.
b. Find the number of insects you catch on Saturday without using an equation. Compare the steps used to solve the equation in part (a) with the steps used to solve the problem in part (b).
c. Describe a problem that is more convenient to solve using an equation. Then describe a problem that is more convenient to solve without using an equation.

Answer:
a. You catch 32 insects on Saturday.
b.
Explanation:
a.
(x – 5)/3 = 9
(x – 5) = 27
x = 27 + 5 = 32
You catch 32 insects on saturday.
b. The only number which is divisible by 3 and obtained after subtracting 5 insects from it is 5. so, you caught 32 insects.
c. Equation is more convenient to solve the problem.
Question 42.
GEOMETRY
How can you change the dimensions of the rectangle so that the ratio of the length to the width stays the same, but the perimeter is 185 centimeters? Write an equation that shows how you found your answer.

Answer:
The required dimensions are 52.75, 52.75, 39.75.
Explanation:
The perimeter for given dimensions = 2(25 + 12) = 50 + 24 = 74
Given perimeter = 185
Change in perimeter = 185 – 74 = 111
Divide the perimeter by 4 = 111/4 = 27.75
Add 27.75 to each dimension to get the perimeter 185
So, the required dimensions are 52.75, 52.75, 39.75
Lesson 4.4 Writing and Graphing Inequalities
EXPLORATION 1
Understanding Inequality Statements
Work with a partner. Create a number line on the floor with both positive and negative numbers.
a. For each statement, stand at a number on your number line that could represent the situation. On what other numbers can you stand?

• Atleast 3 students from our school are in a chess tournament.

• Your ring size is less than 7.5.

• The temperature is no more than -1 degree Fahrenheit.
• The elevation of a frogfish is greater 1 than -8\(\frac{1}{2}\) meters.


b. How can you represent all of the solutions for each statement in part(a) on a number line?
4.4 Lesson
Try It
Write the word sentence as an inequality.
Question 1.
A number is at least -10.
Answer:
n ≥ -10
Explanation:
The symbol for at least is ≥.
So, n ≥ -10
Question 2.
Twice a number y is more than –\(\frac{5}{2}\).
Answer:
2y > -5/2
Explanation:
more than symbol is >.
2y > -5/2
A solution of an inequality is a value that makes the inequality true. An inequality can have more than one solution. The set of all solutions of an inequality is called the solution set.
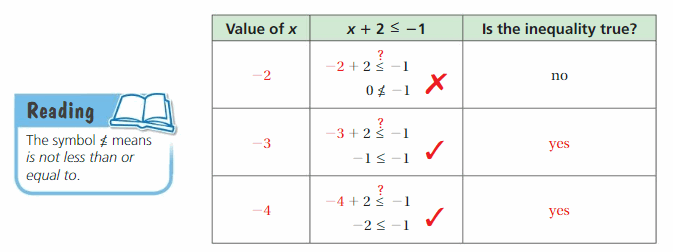
Try It
Tell whether -5 is a solution of the inequality.
Question 3.
x + 12 > 7
Answer:
-5 is not soution.
Explanation:
x + 12 > 7
-5 + 12 > 7
7 > 7
Question 4.
1 – 2p ≤ -9
Answer:
-5 is not the solution.
Explanation:
1 – 2p ≤ -9
1 – 2(-5) ≤ -9
1 + 10 ≤ -9
11 ≤ -9
Question 5.
n ÷ 2.5 ≥ -3
Answer:
-5 is solution.
Explanation:
-5 ÷ 2.5 ≥ -3
-2 ≥ -3
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 6.
REASONING
Do x < 5 and 5 < x represent the same inequality? Explain.
Answer:
No, both inequalities do not represent the same.
Explanation:
No, both inequalities do not represent the same.
The reason is the first one x < 5 means all numbers that are less than 5.
Second one 5 < x, all numbers that are greater than 5.
Question 7.
DIFFERENT WORDS, SAME QUESTION
Which is different? Write “both” inequalities.

Answer:
A number k is no more than -3 is different.
Explanation:
A number k is less than or equal to -3
k ≤ -3
A number k is at least -3
k ≥ – 3
a number k is at most -3
k ≤ -3
A number k is no more than -3
k < -3
CHECKING SOLUTIONS
Tell whether -4 is a solution of the inequality.
Question 8.
c + 6 ≤ 3
Answer:
Yes, -4 is a solution of the inequality.
Explanation:
c + 6 ≤ 3
-4 + 6 ≤ 3
2 ≤ 3
Question 9.
6 > p ÷ (-0.5)
Answer:
No, -4 is not a solution of the inequality.
Explanation:
6 > p ÷ (-0.5)
6 > -4 ÷ (-0.5)
6 > 4 ÷ (0.5)
6 > 8
Question 10.
-7 < 2g + 1
Answer:
No, -4 is not a solution of the inequality.
Explanation:
-7 < 2g + 1
-7 < 2(-4) + 1
-7 < -8 + 1
-7 < -7
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 11.
The three requirements to pass a fitness test are shown. Write and graph three inequalities that represent the requirements. Then give a set of possible values for a person who passes the test.

Answer:
x ≥ 2 kilometers
x ≥ 25 pushups
x ≥ 10 pullups

Explanation:
Jog at least 2 kilometers
x ≥ 2 kilometers
Perform 25 or more pushups
x ≥ 25 pushups
Perform at least 10 pull-ups
x ≥ 10 pullups
Question 12.
To set a depth record, a submersible vehicle must reach a water depth less than -715 feet. A vehicle breaks the record by more than 10 feet. Write and graph an inequality that represents the possible depths reached by the vehicle.
Answer:
-705 < x < -175

Explanation:
Submersible vehicle must reach a water depth less than -715 feet
x < – 175
A vehicle breaks the record by more than 10 feet.
So, -175 + 10 < x < -175
-705 < x < -175
Writing and Graphing Inequalities Homework & Practice 4.4
Review & Refresh
Solve the equation. Check your solution.
Question 1.
p – 8 = 3
Answer:
p = 11
Explanation:
p – 8 = 3
p = 8 + 3
p = 11
Putting p = 11 in p – 8 = 3
11 – 8 = 3
Question 2.
8.7 + w = 5.1
Answer:
w = -3.6
Explanation:
8.7 + w = 5.1
w = 5.1 – 8.7
w = -3.6
Putting w = -3.6 in 8.7 + w = 5.1
8.7 + (-3.6) = 8.7 – 3.6 = 5.1
Question 3.
x – 2 = -9
Answer:
x = -7
Explanation:
x – 2 = -9
x = -9 + 2
x = -7
Putting x = -7 in x – 2 = -9
-7 – 2 = -9
Question 4.
8v + 5 = 1
Answer:
v = -1/2
Explanation:
8v + 5 = 1
8v = 1 – 5
8v = -4
v = -4/8
v = -1/2
Putting v = -1/2 in 8v + 5 = 1
8(-1/2) + 5 = -4 + 5 = 1
Question 5.
![]()
Answer:
n = 5
Explanation:
7/8 – (1/4)n = -3/8
7/8 + 3/8 = 1/4 n
1/4 n = (7 + 3)/8
1/4 n = 10/8
n = (10/8) x (4)
n = 10/2
n = 5
Putting n = 5 in 7/8 – (1/4)n = -3/8
7/8 – (1/4)5 = 7/8 – 5/4
= (7-10)/8 = -3/8
Question 6.
1.8 = 2.1h – 5.7 – 4.6h
Answer:
h = -3
Explanation:
1.8 = 2.1h – 5.7 – 4.6h
1.8 + 5.7 = 2.1h – 4.6h
-2.5h = 7.5
h = -7.5/2.5
h = -3
Putting h = -3 in 1.8 = 2.1h – 5.7 – 4.6h
1.8 = 2.1(-3) – 5.7 – 4.6(-3)
= -6.3 – 5.7 + 13.8
= -12 + 13.8
Question 7.
Which expression has a value less than -5?
A. 5 + 8
B. -9 + 5
C. 1 + (-8)
D. 7 + (-2)
Answer:
B has a value less than -5.
Explanation:
A. 5 + 8 = 13
B. -9 + 5 = -4
C. 1 + (-8) = -7
D. 7 + (-2) = 5
Concepts, Skills, & Problem Solving
UNDERSTANDING INEQUALITY STATEMENTS
Choose a number that could represent the situation. What other numbers could represent the situation? (See Exploration 1, p. 145.)
Question 8.
Visibility in an airplane is greater than 6.5 miles.
Answer:

x > 6.5 miles
Explanation:
x > 6.5 miles
Question 9.
You must sell no fewer than 20 raffle tickets for a fundraiser.
Answer:
x > 20

Explanation:
x > 20
Question 10.
You consume at most 1800 calories per day.
Answer:
x ≤ 1800

Explanation:
x ≤ 1800
Question 11.
The elevation of the Dead Sea is less than -400 meters.
Answer:
x < -400

Explanation:
x < -400
WRITING AN INEQUALITY
Write the word sentence as an inequality.
Question 12.
A number y is no more than -8.
Answer:
y < -8
Explanation:
No more than means <
y < -8
Question 13.
A number w added to 2.3 is more than 18.
Answer:
w + 2.3 > 18
Explanation:
More than means >
w + 2.3 > 18
w > 18 – 2.3
w > 15.7
Question 14.
A number t multiplied by -4 is atleast –\(\frac{2}{5}\).
Answer:
-4t ≥ -2/5
Explanation:
Atleast means ≥
-4t ≥ -2/5
Question 15.
A number b minus 4.2 is less than -7.5.
Answer:
b – 4.2 < -7.5
Explanation:
Less than means <
b – 4.2 < -7.5
b < -7.5 + 4.2
b < -3.3
b > 3.3
Question 16.
–\(\frac{5}{9}\) is no less than 5 times a number k.
Answer:
-5/9 > 5k
Explanation:
No less than means >
-5/9 > 5k
Question 17.
YOU BE THE TEACHER
Your friend writes the word sentence as an inequality. Is your friend correct? Explain your reasoning.

Answer:
My friend is correct.
Explanation:
Twice a number x means 2x
Atmost means ≤
So, 2x ≤ -24
CHECKING SOLUTIONS
Tell whether the given value is a solution of the inequality.
Question 18.
n + 8 ≤ 13; n = 4
Answer:
n = 4 is the solution
Explanation:
4 + 8 ≤ 13
12 ≤ 13
Question 19.
-15 < 5h; h = -5
Answer:
h = -5 is the solution
Explanation:
-15 < 5(-5)
-15 < -25
Question 20.
p + 104 ≤ 0.5; p = 0.1
Answer:
p = 0.1 is the solution
Explanation:
0.1 + 104 ≤ 0.5
104.1 ≤ 0.5
Question 21.
\(\frac{a}{6}\) > -4; a = -18
Answer:
a = -18 is the solution
Explanation:
a/6 > -4
-18/6 > -4
-3 > -4
Question 22.
6 ≥ –\(\frac{2}{3}\)s ; s = -9
Answer:
s = -9 is the solution
Explanation:
6 ≥ (-2/3)s
6 ≥ (-2/3) x -9
6 ≥ 2 x 3
6 ≥ 6
Question 23.
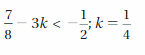
Answer:
k = 1/4 is not the solution
Explanation:
7/8 – 3k < -1/2
7/8 – 3(1/4) < -1/2
7/8 – 3/4 < -1/2
(7 – 6)/8 < -1/2
1/8 < -1/2
GRAPHING AN INEQUALITY
Graph the inequality on a number line.
Question 24.
r ≤ -9
Answer:

Question 25.
g ≥ 2.75
Answer:

Question 26.
![]()
Answer:
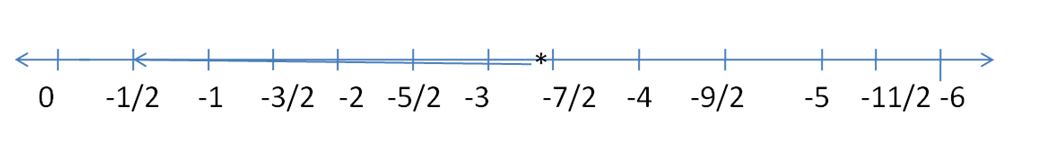
Explanation:
x ≥ -7/2
Question 27.
![]()
Answer:

Explanation:
5/4 > z
Question 28.
MODELING REAL LIFE
Each day at lunchtime, atleast 53 people buy food from a food truck. Write and graph an inequality that represents this situation.
Answer:
Explanation:
CHECKING SOLUTIONS
Tell whether the given value is a solution of the inequality.
Question 29.
4k < k + 8; k = 3
Answer:
Explanation:
Question 30.
![]()
Answer:
Explanation:
Question 31.
7 – 2y > 3y + 13; y = -1
Answer:
Explanation:
Question 32.
![]()
Answer:
Explanation:
Question 33.
PROBLEM SOLVING
A single subway ride for a student costs $1.25. A monthly pass costs $35.
a. Write an inequality that represents the numbers of times you can ride the subway each month for the monthly pass to be a better deal.
b. You ride the subway about 45 times per month. Should you buy the monthly pass? Explain.
Answer:
a. 1.25x ≥ 35
b. Yes, it is better to buy a monthly pass.
Explanation:
A.
1.25x ≥ 35
B. 1.25x ≥ 35
x ≥ 35/1.25
x ≥ 28
Yes, it is better to buy a monthly pass.
Question 34.
LOGIC
Consider the in equality b > -2.
a. Describe the values of b that are solutions of the inequality.
b. Describe the values of b that are not solutions of the inequality. Write an inequality that represents these values.
c. What do all the values in parts (a) and (b) represent? Is this true for any similar pair of inequalities? Explain your reasoning.
Answer:
a. b is greater than -2, The possible solutions of b are -1, 0, 1, 2, and so on
b. The values of b that are nor solutions are -2, -3, -4, -5, -6, …. and an inequality that represents it is b < – 2
c. All the values in parts (A), (b) represents all whole numbers.
Question 35.
MODELING REAL LIFE
A planet orbiting a star at a distance such that its temperatures are right for liquid water is said to be in the star’s habitable zone. The habitable zone of a particular star is atleast 0.023 AU and at most 0.054 AU from the star (1 AU is equal to the distance between Earth and the Sun). Draw a graph that represents the habitable zone.
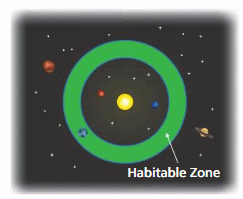
Answer:
x ≥ 0.023 and x ≤ 0.054
Explanation:
As the start is at least 0.023 AU means x ≥ 0.023
And it is almost 0.054 AU means x ≤ 0.054
x ≥ 0.023 ≤ 0.054
Question 36.
DIG DEEPER!
The girth of a package is the distance around the perimeter of a face that does not include the length as a side. A postal service says that a rectangular package can have a maximum combined length and girth of 108 inches.
a. Write an inequality that represents the allowable dimensions for the package.
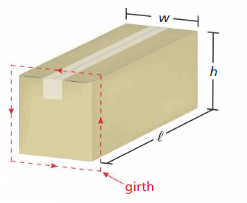
b. Find three different sets of allowable dimensions that are reasonable for the package. Find the volume of each package.
Answer:
a. x ≥ 27 inches
b. The three different sets of allowable dimensions are 27, 28, 29 and their volumes are 19683 cubic inches, 21952 cubic inches, 24389 cubic inches.
Explanation:
Girth = 108 inches
4x ≥ 108
x ≥ 108/4
x ≥ 27
b. The three different sets of allowable dimensions are 27, 28, 29
Volume = 27³ = 19683
= 28³ = 21952
= 29³ = 24389
Lesson 4.5 Solving Inequalities Using Addition or Subtraction
EXPLORATION 1
Writing Inequalities
Work with a partner. Use two number cubes on which the odd numbers are negative on one of the number cubes and the even numbers are negative on the other number cube.

- Roll the number cubes. Write an inequality that compares the numbers.
- Roll one of the number cubes. Add the number to each side of the inequality and record your result.
- Repeat the previous two steps five more times.
a. When you add the same number to each side of an inequality, does the inequality remain true? Explain your reasoning.

b. When you subtract the same number from each side of an inequality, does the inequality remain true? Use inequalities generated by number cubes to justify your answer.
c. Use your results in parts (a) and (b) to make a conjecture about how to solve inequality of form x + a < b for x. 4.5 Lesson Try It Solve the inequality.
Answer:
a. When you add the same number to each side of an inequality, does the inequality remains true. Because when the same quantity is added on both sides does not show any impact on the actual inequality.
b. When you subtract the same number from each side of an inequality, the inequality remain true. Because when the same quantity is subtracted from both sides does not show any impact on the actual inequality.
Graph the solution.
Question 1.
y – 6 > -7
Answer:
y > -1
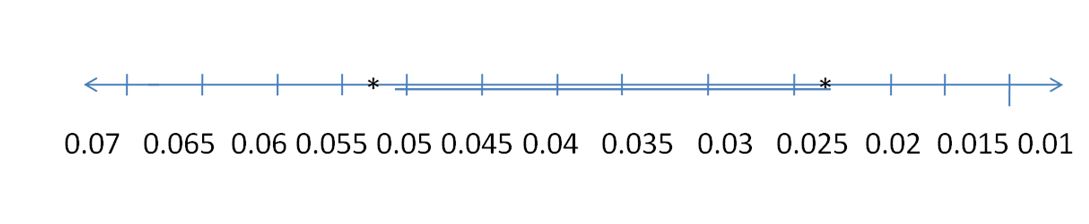
Explanation:
y > -7 + 6
y > -1
Question 2.
b – 3.8 ≤ 1.7
Answer:

Explanation:
b ≤ 1.7 + 3.8
b ≤ 5.5
Question 3.
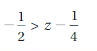
Answer:

Explanation:
-1/2 + 1/4 > z
(-2 + 1)/4 > z
-1/4 > z
1/4 < z
Try It
Solve the inequality. Graph the solution.
Question 4.
w + 3 ≤ -1
Answer:
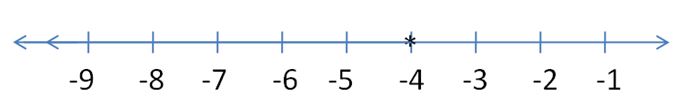
w ≤ -4
Explanation:
w ≤ -1 – 3
w ≤ -4
Question 5.
8.5 ≥ d + 10
Answer:
1.5 ≤ d
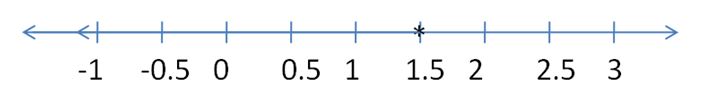
Explanation:
8.5 – 10 ≥ d
-1.5 ≥ d
1.5 ≤ d
Question 6.
![]()
Answer:
x > 3/4

Explanation:
x > 3/2 – 3/4
x > (6 – 3)/4
x > 3/4
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 7.
WRITING
Are the inequalities c + 3 > 5 and c – 1 > 1 equivalent? Explain.
Answer:
Inequalities are equivalent.
Explanation:
c + 3 > 5 and c – 1 > 1
c > 5 – 3 and c > 1 + 1
c > 2 and c > 2
Question 8.
WHICH ONE DOESN’T BELONG?
Which inequality does not belong with the other three? Explain your reasoning.
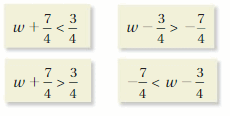
Answer:
-7/4 < w – 3/4
Explanation:
w + 7/4 < 3/4
w < 3/4 – 7/4
w < -4/4
w < -1
w – 3/4 > -7/4
w > -7/4 + 3/4
w > -4/4
w > -1
w+ 7/4 > 3/4
w > 3/4 – 7/4
w > -4/4
w > -1
-7/4 < w – 3/4
-7/4 + 3/4 < w
-4/4 < w
-1 < w
By solving all inequalities we obtain w > -1, but by solving -7/4 < w – 3/4, we get -1 < w.
SOLVING AN INEQUALITY
Solve the inequality. Graph the solution.
Question 9.
x – 4 > -6
Answer:

x > -2
Explanation:
x > -6 + 4
x > -2
Question 10.
z + 4.5 ≤ 3.25
Answer:
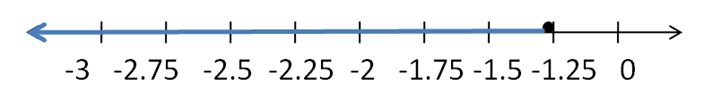
z ≤ -1.25
Explanation:
z ≤ 3.25 – 4.5
z ≤ -1.25
Question 11.
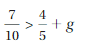
Answer:
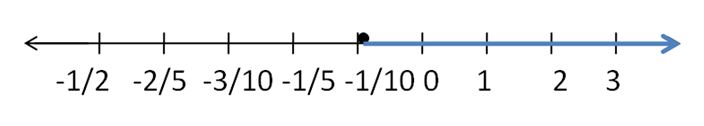
-1/10 > g
Explanation:
7/10 – 4/5 > g
(7 – 8)/10 > g
-1/10 > g
Question 12.
OPEN-ENDED
Write two different inequalities that can be represented using the graph. Justify your answers.
Answer:
x > -5
x ≥ 5
Explanation:
x > -5
Because in the graph the point is from 5 to left side.
x ≥ 5
In the graph, the point is also located on 5.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 13.
DIG DEEPER!
A volcanologist rappels 1200 feet into a volcano. He wants to climb out of the volcano in less than 4 hours. He climbs the first 535 feet in 100 minutes. Graph an inequality that represents the average rates at which he can climb the remaining distance and meet his goal. Justify your answer.
Answer:
The average rate at which he climb the remaining distance and meet his goal is less than 0.21 inches per 1 minute.

Explanation:
A volcanologist rappel climbs first 535 feet in 100 minutes
He needs to climb the remaining 1200 – 535 = 665 feet in the remaining time.
(1200 – 535)x < (4 x 60 – 100)
665x < (240 – 100)
665x < 140
x < 140/665
x < 0.21
The average rate at which he climb the remaining distance and meet his goal is less than 0.21 inches per 1 minute.
Question 14.
You install a mailbox by burying a post as shown. According to postal service guidelines, the bottom of the box must be at least 41 inches, but no more than 45 inches, above the road. Write and interpret two inequalities that describe the possible lengths of the post.

Answer:
The possible length of post is in between 45 to 41 inches
Explanation:
Given that,
The bottom box must be at least 41 inches
x ≥ 41 inches
The bottom box must be no more than 45 inches
x < 45
By combining both inequalities, we get
45 < x ≥ 41
So, the possible length of post is in between 45 to 41 inches.
Solving Inequalities Using Addition or Subtraction Homework & Practice 4.5
Review & Refresh
Write the word sentence as an inequality.
Question 1.
A number p is greater than 5.
Answer:
p > 5.
Explanation:
greater than means >
p > 5.
Question 2.
A number z times 3 is atmost -4.8.
Answer:
3z ≤ -4.8
Explanation:
Atmost means ≤
3z ≤ -4.8
Question 3.
The sum of a number n and \(\frac{2}{3}\) is no less than 5\(\frac{1}{3}\).
Answer:
n + 2/3 > 5(1/3)
Explanation:
The sum of n and 2/3 is n + 2/3
no less than means >
n + 2/3 > 5(1/3)
Solve the equation. Check your solution.
Question 4.
4x = 36
Answer:
x = 9
Explanation:
4x = 36
x = 36/4
x = 9
Putting x = 9 in 4x = 36
4(9) = 36
Question 5.
\(\frac{w}{3}\) = -9
Answer:
w = -27
Explanation:
w/3 = -9
w = -9 x 3
w = -27
Putting w = -27 in w/3 = -9
-27/3 = -9
Question 6.
-2b = 44
Answer:
b = -22
Explanation:
-2b = 44
b = -44/2
b = -22
Putting b = -22 in -2b = 44
-2(-22) = 44
Question 7.
60 = \(\frac{3}{4}\)h
Answer:
h = 80
Explanation:
60 = (3/4)h
60 x 4 = 3h
240 = 3h
h = 240/3
h = 80
Putting h = 80 in 60 = (3/4)h
60 = (3/4) x 80 = 3 x 20
Question 8.
Which fraction is equivalent to -2.4?

Answer:
-12/5 is the equivalent to -2.4
Explanation:
-12/5 = -2.4
-51/25 = -2.04
-8/5 = -1.6
-6/25 = -0.24
So, by observing all those, we can say that -12/5 is the equivalent to -2.4
Concepts, Skills, & Problem Solving
WRITING AN INEQUALITY
Write an inequality that compares the given numbers. Does the inequality remain true when you add 2 to each side? Justify your answer. (See Exploration 1, p. 151.)
Question 9.
-1; 4
Answer:
-1 > 4
False.
Explanation:
-1 > 4
-1 + 2 > 4 + 2
1 > 6
Question 10.
-3; -6
Answer:
-3 > – 6
True
Explanation:
-3 > – 6
By adding 2 to each side
-3 + 2 > -6 + 2
-1 > -4
Question 11.
-4; -1
Answer:
-4 < -1
False
Explanation:
-4 < -1
-4 + 2 < -1 + 2
-2 < 1
False
SOLVING AN INEQUALITY
Solve the inequality. Graph the solution.
Question 12.
x + 7 ≥ 18
Answer:
x ≥ 11

Explanation:
x ≥ 18 – 7
x ≥ 11
Question 13.
a – 2 > 4
Answer:
a > 6

Explanation:
a > 4 + 2
a > 6
Question 14.
3 ≤ 7 + g
Answer:
-4 ≤ g

Explanation:
3 – 7 ≤ g
-4 ≤ g
Question 15.
8 + k ≤ -3
Answer:
k ≤ -11

Explanation:
k ≤ -3 – 8
k ≤ -11
Question 16.
-12 < y – 6
Answer:
-6 < y
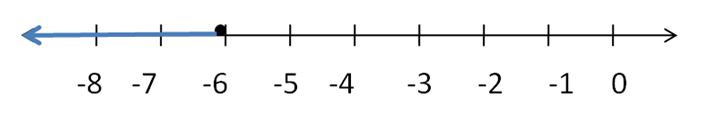
Explanation:
-12 + 6 < y
-6 < y
Question 17.
n – 4 < 5
Answer:
n < 9

Explanation:
n < 4 + 5
n < 9
Question 18.
t – 5 ≤ -7
Answer:
t ≤ -2

Explanation:
t ≤ -7 + 5
t ≤ -2
Question 19.
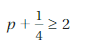
Answer:
p ≥ 7/4

Explanation:
p ≥ 2 – (1/4)
p ≥ (8 – 1)/4
p ≥ 7/4
Question 20.
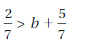
Answer:
-3/7 > b
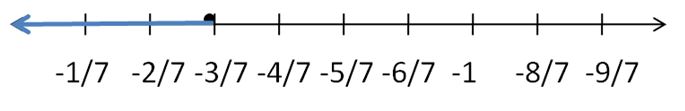
Explanation:
2/7 – 5/7 > b
(2 – 5)/7 > b
-3/7 > b
Question 21.
z – 4.7 ≥ -1.6
Answer:
z ≥ 3.1

Explanation:
z ≥ -1.6 + 4.7
z ≥ 3.1
Question 22.
-9.1 < d – 6.3
Answer:
-2.8 < d

Explanation:
-9.1 + 6.3 < d
-2.8 < d
Question 23.

Answer:
-4/5 > s
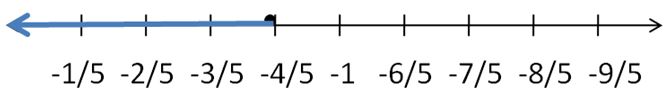
Explanation:
8/5 – 12/5 > s
(8 – 12)/5 > s
-4/5 > s
Question 24.
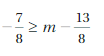
Answer:
6/8 ≥ m

Explanation:
-7/8 + 13/8 ≥ m
6/8 ≥ m
Question 25.
r + 0.2 < -0.7
Answer:
r < 0.5
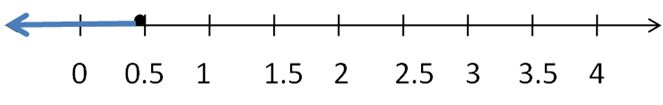
Explanation:
r < 0.7 – 0.2
r < 0.5
Question 26.
h – 6 ≤ -8.4
Answer:
h ≤ -2.4
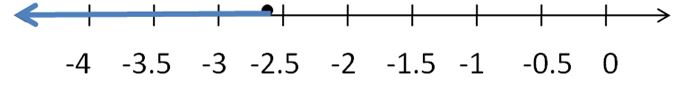
Explanation:
h ≤ -8.4 + 6
h ≤ -2.4
YOU BE THE TEACHER
Your friend solves the inequality and graphs the solution. Is your friend correct? Explain your reasoning.
Question 27.

Answer:
My friend is correct.
Explanation:
x – 7 > – 2
x > – 2 + 7
x > 5
As the graph says the values of x are more than 5.
So, my friend is correct.
Question 28.

Answer:
My friend is correct.
Explanation:
8 ≤ x + 3
8 – 3 ≤ x
5 ≤ x
As the graph represents the values of x are less than or equal to 5.
So, my friend is correct.
Question 29.
MODELING REAL LIFE
A small airplane can hold 44 passengers. Fifteen passengers board the plane.
a. Write and solve an inequality that represents the additional numbers of passengers that can board the plane.
b. Can 30 more passengers board the plane? Explain.
Answer:
a. 15 + x ≤ 44
b. No.
Explanation:
As the airplane can hold 44 passengers and already 15 passengers board the plane. The inequality can be expressed as
15 + x ≤ 44
Here, x is the additional number of passengers who board the plane
b. Can 30 more passengers board the plane
So, take x as 30
15 + 30 ≤ 44
45 ≤ 44
As this inequality is false. So, 30 more passengers board the plane
GEOMETRY
Find the possible values of x.
Question 30.
The perimeter is less than 28 feet.
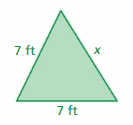
Answer:
x < 14
Explanation:
Perimeter = 7 + 7 + x = 14 + x
The perimeter is less than 28 feet.
So, p < 28
14 + x < 28
x < 28 – 14
x < 14
Question 31.
The base is greater than the height.
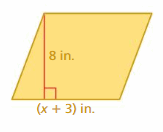
Answer:
x > 5
Explanation:
Here base = (x + 3), h = 8
The base is greater than the height.
b > h
(x + 3) > 8
x > 8 – 3
x > 5
Question 32.
The perimeter is less than or equal to 51 meters.
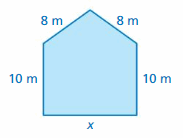
Answer:
x ≤ 15 m
Explanation:
Perimeter = 10 + 8 + 8 + 10 + x
= 36 + x
The perimeter is less than or equal to 51 meters.
perimeter ≤ 51
36 + x ≤ 51
x ≤ 51 – 36
x ≤ 15
Question 33.
REASONING
The inequality d + s > -3 is equivalent to d > -7. What is the value of s?
Answer:
s = -4
Explanation:
d + s > -3
d > -3 – s
When s = -4, then d + s > -3 is equivalent to d > -7
So, s = -4
Question 34.
LOGIC
You can spend up to $35 on a shopping trip.
a. You want to buy a shirt that costs $14. Write and solve an inequality that represents the remaining amounts of money you can spend if you buy the shirt.
b. You notice that the shirt is on sale for 30% off. How does this change your inequality in part(a)?

Answer:
a. x + $14 < 35
b. x + $9.8 < 35
Explanation:
You can spend up to $35 on a shopping trip.
a. Shirt cost = $14
The inequality represents the remaining amounts of money you can spend if you buy the shirt.
x + $14 < 35
b. When the shirt is on 30% sale
If the shirt is on sale, then the cost of the shirt is $9.8
Then 35 – 9.8 = 25.2
Then the inequality is x + $9.8 < 35
Question 35.
DIG DEEPER!
If items plugged into a circuit use more than 2400 watts of electricity, the circuit overloads. A portable heater that uses 1050 watts of electricity is plugged into the circuit.
a. Find the additional numbers of watts you can plug in without overloading the circuit.
b. In addition to the portable heater, what two other items in the table can you plug in at the same time without overloading the circuit? Is there more than one possibility? Explain.
Answer:
a. You can add 1350 additional watts without overloading the circuit.
b. You can add vacuum cleaner, television, and vacuum cleaner, aquarium.
Explanation:
a. Given that,
Circuit overloads at 2400 watts
Electricity used by heater = 1050 watts
Let,
x be the number of additional watts.
Electricity used by heater + Additional watts ≤ Circuit’s capacity
1050 + x ≤ 2400
x ≤ 2400 – 1050
x ≤ 1350
You can add 1350 additional watts without overloading the circuit.
b. Check the sum of which two numbers is less than 1350
You can add vacuum cleaner, television, and vacuum cleaner, aquarium.
Question 36.
The possible values of x are given by x + 8 ≤ 6. What is the greatest possible value of 7x? Explain your reasoning.
Answer:
The greatest possible value of x is -14.
Explanation:
Given that,
x + 8 ≤ 6
x ≤ 6 – 8
x ≤ -2
Multiply both sides by 7
7x ≤ -14
So the greatest possible value of x is -14.
Lesson 4.6 Solving Inequalities Using Multiplication or Division
EXPLORATION 1
Writing Inequalities
Work with a partner. Use two number cubes on which the odd numbers are negative on one of the number cubes and the even numbers are negative on the other number cube.

- Roll the number cubes. Write an inequality that compares the numbers.
- Roll one of the number cubes. Multiply each side of the inequality by the number and record your result.
- Repeat the previous two steps nine more times.
a. When you multiply each side of an inequality by the same number, does the inequality remain true? Explain your reasoning.

b. When you divide each side of an inequality by the same number, does the inequality remain true? Use inequalities generated by number cubes to justify your answer.
c. Use your results in parts (a) and (b) to make a conjecture about how to solve an inequality of the form ax < b for x when a > 0 and when a < 0.
4.6 Lesson
Try It
Solve the inequality. Graph the solution.
Question 1.
n ÷ 3 < 1
Answer:
n < 3
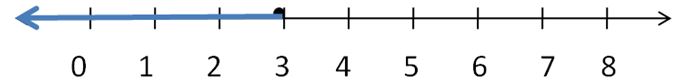
Explanation:
n < 1 x 3
n < 3
Question 2.
![]()
Answer:
-5 ≤ m

Explanation:
-0.5 x 10 ≤ m
-5 ≤ m
Question 3.
![]()
Answer:
-4.5 > p

Explanation:
-3 > (2/3) p
-3 x 3 > 2p
-9 > 2p
-9/2 > p
-4.5 > p
Try It
Solve the inequality. Graph the solution.
Question 1.
4b ≥ 2
Answer:
b ≥ 1/2

Explanation:
4b ≥ 2
b ≥ 2/4
b ≥ 1/2
Question 5.
12k ≤ -24.
Answer:
k ≤ -2
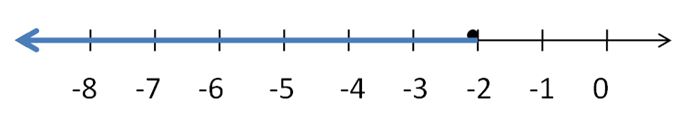
Explanation:
12k ≤ -24
k ≤ -24/12
k ≤ -2
Question 6.
-15 < 2.5q
Answer:
-6 < q

Explanation:
-15 < 2.5q
-15/2.5 < q
-6 < q
Try It
Solve the inequality. Graph the solution.
Question 7.
![]()
Answer:
x > 12

Explanation:
x > -4 x -3
x > 12
Question 8.
![]()
Answer:
1 ≥ y
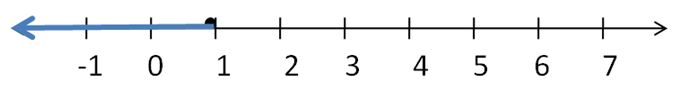
Explanation:
0.5 ≤ -y/2
0.5 x 2 ≤ -y
1 ≤ – y
1 ≥ y
Question 9.
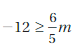
Answer:
-10 ≥ m
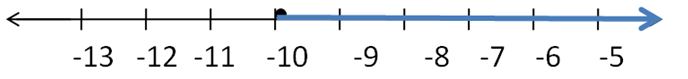
Explanation:
-12 ≥ (6/5)m
-12 x 5 ≥ 6m
-60 ≥ 6m
-60/6 ≥ m
-10 ≥ m
Question 10.
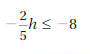
Answer:
h ≤ 20

Explanation:
(-2/5)h ≤ -8
(2/5)h ≤ 8
2h ≤ 8 x 5
2h ≤ 40
h ≤ 40/2
h ≤ 20
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 11.
OPEN-ENDED
Write an inequality that you can solve using the Division Property of Inequality where the direction of the inequality symbol must be reversed.
Answer:
Let us take an inequality -3x < 6
Divide both sides by -3
-3x/-3 < 6/-3
x > -2
The solution is x > -2
Question 12.
PRECISION
Explain how solving 4x < -16 is different from −4x < 16.
Answer:
4x < -16
x < -16/4
x < -4
−4x < 16
-4x/-4 > 16/-4
x > -4
For 4x < -16, we get x < -4. For −4x < 16 we get x > -4 as solution.
SOLVING AN INEQUALITY
Solve the inequality. Graph the solution.
Question 13.
6n < -42
Answer:
n < -7
Explanation:
6n < -42
Divide both sides by 6
6n/6 < -42/6
n < -7
Question 14.
![]()
Answer:
32 ≤ g

Explanation:
4 ≥ -g/8
4 x 8 ≥ -g
32 ≥ -g
32 ≤ g
Question 15.
WRITING
Are the inequalities 12c > -15 and 4c < -5 equivalent? Explain.
Answer:
Both inequalities are not equivalent.
Explanation:
12c > -15
c > -15/12
c > -5/4
4c < -5
c < -5/4
So, both inequalities are not equivalent
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 16.
DIG DEEPER!
You want to put up a fence that encloses a triangular region with an area greater than or equal to 60 square feet. Describe the possible values of c.
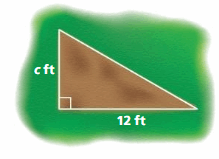
Answer:
12 + c + √(c² + 144) ≥ 60
Explanation:
Find all sides to get its perimeter
Let us take hypotenuse as x.
Asit is a right-angled triangle, hypotenuse² = sum of squares of other sides
x² = c² + 12²
x² = c² + 144
x = √(c² + 144)
The perimeter of the triangular region is greater than or equal to 60 square feet.
So, perimeter ≥ 60
Perimeter = 12 + c + x = 12 + c + √(c² + 144)
12 + c + √(c² + 144) ≥ 60
Question 17.
A motorcycle rider travels at an average speed greater than 50 miles per hour. Write and solve an inequality to determine how long it will take the motorcycle rider to travel 375 miles. Explain your reasoning.

Answer:
It may take more than 7.5 hours for a motorcycle rider to travel 375 miles
Explanation:
A motorcycle rider travels at an average speed greater than 50 miles per hour.
speed > 50 miles per hour
50 miles per one hour
So, 375 miles per how many hours
50x > 375
x >375/50
x > 7.5
So, it may take more than 7.5 hours for a motorcycle rider to travel 375 miles
Solving Inequalities Using Multiplication or Division Homework & Practice 4.6
Review & Refresh
Solve the inequality. Graph the solution.
Question 1.
h + 4 < 6
Answer:
h < 2
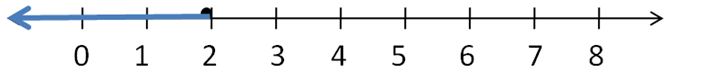
Explanation:
h < 6 – 4
h < 2
Question 2.
c – 5 ≥ 4
Answer:
c ≥ 9

Explanation:
c ≥ 4 + 5
c ≥ 9
Question 3.
![]()
Answer:
-1/10 ≤ n
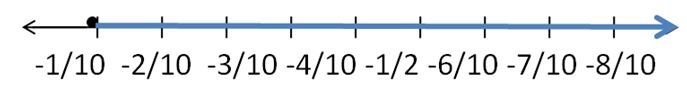
Explanation:
7/10 ≤ n + 4/5
7/10 – 4/5 ≤ n
(7 – 8)/10 ≤ n
-1/10 ≤ n
Solve the equation. Check your solution.
Question 4.
-2w + 4 = -12
Answer:
w = 4
Explanation:
-2w = -12 + 4
-2w = -8
2w = 8
w = 8/2
w = 4
Putting w = 4 in -2w = -12 + 4
-2(-4) = -12 + 4
-8 = -8
Question 5.
![]()
Answer:
v = 45
Explanation:
v/5 = 3 + 6 = 9
v = 9 x 5
v = 45
Putting v = 45 in v/5 – 6 = 3
45/5 – 6 = 9 – 6 = 3
Question 6.
3(x – 1) = 18
Answer:
x = 7
Explanation:
3(x – 1) = 18
(x – 1) = 18/3
x – 1 = 6
x = 6 + 1
x = 7
Putting x = 7 in 3(x – 1) = 18
3(7 – 1) = 3 x 6 = 18
Question 7.
![]()
Answer:
m = 4
Explanation:
m/4 + 50 = 51
m/4 = 51 – 50
m/4 = 1
m = 1 x 4
m = 4
Putting m = 4 in m/4 + 50 = 51
4/4 + 50 = 1 + 50 = 51
Question 8.
What is the value of 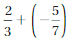 ?
?

Answer:
B.
Explanation:
2/3 + (-5/7) = 2/3 – 5/7
= (14 – 15)/21
= -1/21
Concepts, Skills, & Problem Solving
WRITING AN INEQUALITY
Write an inequality that compares the given numbers. Does the inequality remain true when you multiply each number in the inequality by 2? by -2? Justify your answers. (See Exploration 1, p. 157.)
Question 9.
-2; 5
Answer:
True
Explanation:
-2 < 5
-2 x 2 < 5 x 2
-4 < 10
Question 10.
4; -1
Answer:
true
Explanation:
4 > -1
4 x 2 > -1 x 2
8 > -2
Question 11.
6; -3
Answer:
True
Explanation:
6 > -3
6 x 2 > -3 x 2
12 > -6
SOLVING AN INEQUALITY
Solve the inequality. Graph the solution.
Question 12.
2n > 20
Answer:
n > 10
Explanation:
2n > 20
n > 20/2
n > 10
Question 13.
![]()
Answer:
c ≤ -36
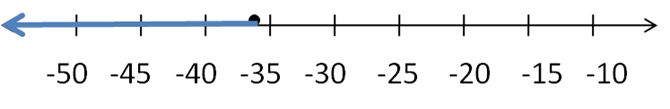
Explanation:
c/9 ≤ -4
c ≤ -4 x 9
c ≤ -36
Question 14.
2.2m < 11
Answer:
m < 5

Explanation:
m < 11/2.2
m < 5
Question 15.
-16 > x ÷ 2
Answer:
-32 > x
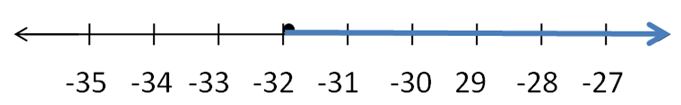
Explanation:
-16 > x ÷ 2
-16 x 2 > x
-32 > x
Question 16.
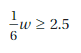
Answer:
w ≥ 15

Explanation:
(1/6)w ≥ 2.5
w ≥ 2.5 x 6
w ≥ 15
Question 17.
7 < 3.5k
Answer:
2 < k

Explanation:
7/3.5 < k
2 < k
Question 18.
![]()
Answer:
x < -5/12

Explanation:
3x ≤ -5/4
x < (-5/4) x (1/3)
x < -5/12
Question 19.
4.2y ≤ -12.6
Answer:
y ≤ -3

Explanation:
4.2y ≤ -12.6
y ≤ -12.6/4.2
y ≤ -3
Question 20.
![]()
Answer:
48.59 > b

Explanation:
11.3 > (b/4.3)
11.3 x 4.3 > b
48.59 > b
Question 21.
MODELING REAL LIFE
You earn $9.20 per hour at your summer job. Write and solve an inequality that represents the numbers of hours you can work to earn enough money to buy a smart phone that costs $299.
Answer:
9.2h ≥ 299
h ≥ 32.5
Explanation:
Let us take h as the number of hours you work.
Multiply the number of hours by the amount you make per hour. If the total is greater than or equal to the cost of the phone, you can buy it.
9.2h ≥ 299
h ≥ 299/9.2
h ≥ 32.5
Question 22.
DIG DEEPER!
You have $5.60 to buy avocados for a guacamole recipe. Avocados cost $1.40 each.
a. Write and solve an inequality that represents the numbers of avocados you can buy.
b. Are there infinitely many solutions in this context? Explain.

Answer:
a. You can buy at most 4 avocados.
b. Yes
Explanation:
Let x represents the number of avocados that you buy
Then 1.40x is the total cost of avocados.
Since you have $5.60 to spend, 1.40x ≤ 5.60
x ≤ 5.60/1.40
x ≤ 4
You can buy at most 4 avocados.
SOLVING AN INEQUALITY
Solve the inequality. Graph the solution.
Question 23.
5n ≥ 15
Answer:
n ≥ 3

Explanation:
5n ≥ 15
n ≥ 15/5
n ≥ 3
Question 24.
7w > -49
Answer:
w > -7

Explanation:
7w > -49
w > -49/7
w > -7
Question 25.
![]()
Answer:
h ≤ -24

Explanation:
-1/3 h ≥ 8
h ≤ -8 x 3
h ≤ -24
Question 26.
![]()
Answer:
45 > x

Explanation:
-9 < -1/5 x
-9 x -5 > x
45 > x
Question 27.
-3y < -14
Answer:
y > 42
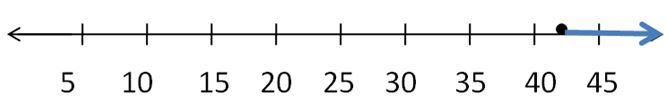
Explanation:
-3y < -14
y > -14 x -3
y > 42
Question 28.
-2d ≥ 26
Answer:
d ≤ -13
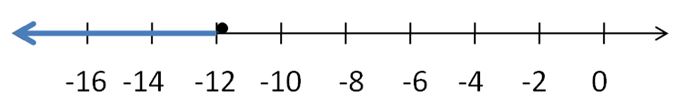
Explanation:
-2d ≥ 26
d ≤ -26/2
d ≤ -13
Question 29.
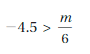
Answer:
-27 > m

Explanation:
-4.5 > m/6
-4.5 x 6 > m
-27 > m
Question 30.
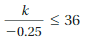
Answer:
k ≥ -144
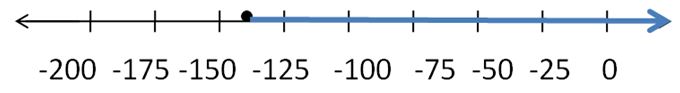
Explanation:
k/(-0.25) ≤ 36
k ≥ -36/0.25
k ≥ -144
Question 31.
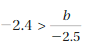
Answer:

6 < b
Explanation:
-2.4 > b/(-2.5)
-2.4 x -2.5 < b
6 < b
YOU BE THE TEACHER
Your friend solves the inequality. Is your friend correct? Explain your reasoning.
Question 32.
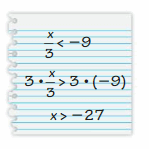
Answer:
Wrong.
Explanation:
x/3 < -9
x < -9 x 3
x < -27
Question 33.

Answer:
Wrong
Explanation:
-3m ≥ 9
m ≤ -9/3
m ≤ -3
WRITING AND SOLVING AN INEQUALITY
Write the word sentence as an inequality. Then solve the inequality.
Question 34.
The quotient of a number and -4 is atmost 5.
Answer:
x ≥ -20
Explanation:
x/-4 ≤ 5
x ≥ 5 x -4
x ≥ -20
Question 35.
A number p divided by 7 is less than -3.
Answer:
p < -21
Explanation:
p/7 < -3
p < -3 x 7
p < -21
Question 36.
Six times a number w is atleast -24.
Answer:
w ≥ -4
Explanation:
6w ≥ -24
w ≥ -24/6
w ≥ -4
Question 37.
The product of -2 and a number is greater than 30.
Answer:
x < -15
Explanation:
-2x > 30
x < -30/2
x < -15
Question 38.
\(\frac{3}{4}\) is greater than or equal to a number k divided by -8.
Answer:
-6 ≤ k
Explanation:
3/4 ≥ k / -8
(3/4) x -8 ≤ k
3 x -2 ≤ k
-6 ≤ k
Question 39.
MODELING REAL LIFE
A cryotherapy chamber uses extreme cold to reduce muscle soreness. A chamber is currently 0°F. The temperature in the chamber is dropping 2.5°F every second. Write and solve an inequality that represents the numbers of seconds that can pass for the temperature to drop below -20°F.

Answer:
8x ≤ -20°F
Explanation:
The temperature in the chamber is dropping 2.5°F every second.
The chamber is currently 0°F.
So, for the 1st second the temperature is -2.5°F
For the second the temperature is -5°F
By calculating these seconds, we get for the 8th second the temperature dropped is below -20°F.
So, the inequality can be 8x ≤ -20°F.
Question 40.
MODELING REAL LIFE
You are moving some of your belongings into a storage facility.
a. Write and solve an inequality that represents the numbers of boxes that you can stack vertically in the storage unit.12.5
b. Can you stack 6 boxes vertically in the storage unit? Explain.
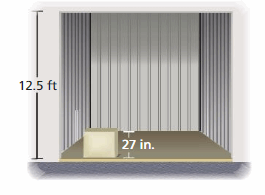
Answer:
a. 27x ≤ 150
b. No
Explanation:
Given that the height of the storage unit is 12.5 feet = 150 inches
The height of each box is 27 inches
Let us take x as the number of boxes that you can stack vertically in the storage unit.
So, 27x ≤ 150
x ≤ 150/27
x ≤ 5.55
b. By solving the inequality, we obtain value as 5.55
So, we can stack only 5 boxes in the stack.
GEOMETRY
Write and solve an inequality that represents x.
Question 41.
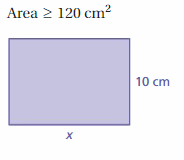
Answer:
x ≥ 12
Explanation:
10x ≥ 120
x ≥ 120/10
x ≥ 12
Question 42.
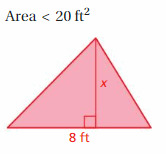
Answer:
x < 5
Explanation:
1/2 * 8 * x < 20
4x < 20
x < 20/4
x < 5
Question 43.
MODELING REAL LIFE
A device extracts no more than 37 liters of water per day from the air. How long does it take to collect atleast 185 liters of water? Explain your reasoning.
Answer:
It takes 5 days to collect atleast 185 liters of water
Explanation:
A device extracts no more than 37 liters of water per day from the air.
Let us take x as the number of days required to collect 185 liters of water.
So, 37x ≥ 185
x ≥ 185/37
x ≥ 5
So, it takes 5 days to collect atleast 185 liters of water
Question 44.
REASONING
Students in a science class are divided into 6 equal groups with atleast 4 students in each group for a project. Describe the possible numbers of students in the class.
Answer:
The possible number of students in the class are 24 or more.
Explanation:
Students in a science class are divided into 6 equal groups with at least 4 students in each group for a project.
So, each group must have 4 or more students.
If we take each group has 4 students, then the number of students is 6 x 4 = 24
So, The possible number of students in the class are 24 or more.
Question 45.
PROJECT
Choose two novels to research.
a. Use the Internet to complete the table below.
b. Use the table to find and compare the average number of copies sold per month for each novel. Which novel do you consider to be the most successful? Explain.
c. Assume each novel continues to sell at the average rate. For what numbers of months will the total number of copies sold exceed twice the current number sold for each novel?


Answer:

b. As the number of copies sold is highest for Jude the Obscure so i consider it as the most successful
c. It purely depends on the number of copies sold.
Question 46.
LOGIC
When you multiply or divide each side of an inequality by the same negative number, you must reverse the direction of the inequality symbol. Explain why.
Answer:
When divide or multiply the same negative number on each side of the inequality, then you need to reverse the direction of the inequality symbol. The reason behind this is, when you take an example and show it on the number line then you can understand easily.
NUMBER SENSE
Describe all numbers that satisfy both inequalities. Include a graph with your description.
Question 47.
4m > -4 and 3m < 15
Answer:
m > -1 and m < 5
Explanation:
4m > -4 and 3m < 15
m > -4/4 and m < 15/3
m > -1 and m < 5
The possible values 4, 3, 2, 1, 0
Question 48.
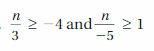
Answer:
n ≥ -12 and n ≤ -5
Explanation:
n/3 ≥ -4 and n/-5 ≥ 1
n ≥ – 4 x 3 and n ≤ 1 x -5
n ≥ -12 and n ≤ -5
The possible values of n are -11, -10, -9, -8, -7, -6.
Question 49.
2x ≥ -6 and 2x ≥ 6
Answer:
x ≥ -3 and x ≥ 3

Explanation:
2x ≥ -6 and 2x ≥ 6
x ≥ -6/2 and x ≥ 6/2
x ≥ -3 and x ≥ 3
The possible values of x are -3, -2, -1, 0, 1, ….
Question 50.
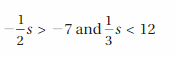
Answer:
s < 14 & s < 36

Explanation:
-1/2 s > -7 and 1/3 s < 12
-s > -7 x 2 and s < 12 x 3
-s > -14 & s < 36
s < 14 & s < 36
Lesson 4.7 Solving Two-Step Inequalities
EXPLORATION 1
Using Algebra Tiles to Solve Inequalities
Work with a partner.
a. What is being modeled by the algebra tiles below? What is the solution?
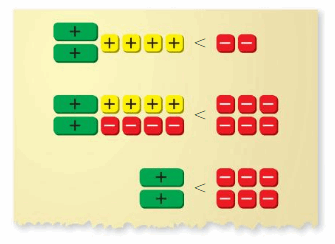
b. Use properties of inequality to solve the original inequality in part(a). How do your steps compare to the steps performed with algebra tiles?
c. Write the three inequalities modeled by the algebra tiles below. Then solve each inequality using algebra tiles. Check your answer using properties of inequality.
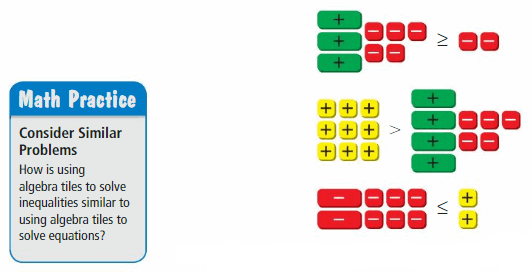
d. Explain how solving a two-step inequality is similar to solving a two-step equation.
4.7 Lesson
Try It
Solve the inequality. Graph the solution.
Question 1.
6y – 7 > 5
Answer:
y > 2

Explanation:
6y – 7 > 5
6y > 7 + 5
6y > 12
y > 12/6
y > 2
Question 2.
4 – 3d ≥ 19
Answer:
d ≤ -5

Explanation:
4 – 3d ≥ 19
-3d ≥ 19 – 4
-3d ≥ 15
d ≤ -15/3
d ≤ -5
Question 3.
![]()
Answer:
w < -4

Explanation:
w/-4 + 8 > 9
w/-4 > 9 – 8
w/-4 > 1
w < 1 x -4
w < -4
Try It
Solve the inequality. Graph the solution.
Question 4.
2(k – 5) < 6
Answer:
k < 8

Explanation:
2(k – 5) < 6
(k – 5) < 6/2
(k – 5) < 3
k < 3 + 5
k < 8
Question 5.
-4(n – 10) < 32
Answer:
n > 2

Explanation:
-4(n – 10) < 32
(n – 10) > -32/4
(n – 10) > -8
n > -8 + 10
n > 2
Question 6.
-3 ≤ 0.5(8 + y)
Answer:
-14 ≤ y

Explanation:
-3 ≤ 0.5(8 + y)
-3/0.5 ≤ (8 + y)
-6 ≤ (8 + y)
-6 – 8 ≤ y
-14 ≤ y
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
SOLVING AN INEQUALITY
Solve the inequality. Graph the solution.
Question 7.
3d – 7 ≥ 8
Answer:
d ≥ 5
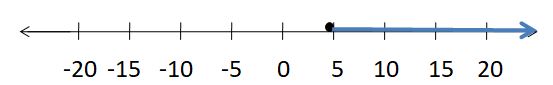
Explanation:
3d – 7 ≥ 8
3d ≥ 8 + 7
3d ≥ 15
d ≥ 15/3
d ≥ 5
Question 8.
![]()
Answer:
-14 < z

Explanation:
-6 – 1 > z/-2
-7 > z/-2
-7 x -2 < z
-14 < z
Question 9.
-6(g + 4) ≤ 12
Answer:
g ≥ -6
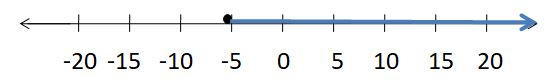
Explanation:
-6(g + 4) ≤ 12
(g + 4) ≥ -12/6
g + 4 ≥ -2
g ≥ -2 – 4
g ≥ -6
Question 10.
OPEN-ENDED
Describe two different ways to solve the inequality 3(a + 5) < 9.
Answer:
a < -3
Explanation:
3(a + 5) < 9
divide both sides by 3
a + 5 < 9/3
a + 5 < 3
Subtract 5 from both sides
a + 5 – 5 < 3 – 5
a < -2
3(a + 5) < 9
expand 3
3a + 15 < 9
3a < 9 – 15
3a < -6
a < -6/2
a < -3
Question 11.
WRITING
Are the inequalities -6x + 18 ≤ 12 and 2x – 4 ≤ -2 equivalent? Explain.
Answer:
Yes, both inequalities are equivalent
Explanation:
-6x + 18 ≤ 12 and 2x – 4 ≤ -2
-6x ≤ 12 – 18 and 2x ≤ -2 + 4
-6x ≤ -6 and 2x ≤ 2
x ≥ -6/6 and x ≤ 2/2
x ≥ -1 and x ≤ 1
Yes, both inequalities are equivalent
Question 12.
OPEN-ENDED
Write a two-step inequality that can be represented by the graph. Justify your answer.
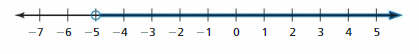
Answer:
x + a > -5 + a
Explanation:
The solution should be x > -5
Add any number to both sides
x + a > -5 + a
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 13.
A fair rents a thrill ride for $3000. It costs $4 to purchase a token for the ride. Write and solve an inequality to determine the numbers of ride tokens that can be sold for the fair to make a profit of at least $750.

Answer:
The number of ride tokens that can be sold for the fair to make a profit of at least $750 is 937
Explanation:
A fair rents a thrill ride for $3000. It costs $4 to purchase a token for the ride.
So, 3000/4 = 750 ride tokens can be sold without loss or profit.
The number of ride tokens that can be sold for the fair to make a profit of at least $750.
So, the total amount collected at the fair is 3000 + 750 = 3750
Each ticket cost 4.
4x ≥ 3750
x ≥ 3750/4
x ≥ 937.5
So, The number of ride tokens that can be sold for the fair to make a profit of at least $750 is 937
Question 14.
DIG DEEPER!
A theater manager predicts that 1000 tickets to a play will be sold if each ticket costs $60. The manager predicts that 20 less tickets will be sold for every $1 increase in price. For what prices can the manager predict that at least 800 tickets will be sold?
Answer:
The manager predict that at least 800 tickets will be sold for $ 70.
Explanation:
The 1000 tickets will be sold when each ticket costs $60.
The manager wants to sell at least 800 tickets which is maximum
1000 – 800 = 200 tickets less than 1000.
Given that for 20 less tickets will be sold for every $1 increase in price.
So, 20 x 2 = 40 less tickets will be sold for $1 x 2 = $2 increase in price.
Proceeding in a similar way, for any natural number n:
20 x n less tickets will be sold for $1 x n=$n increase in price.
Here, 200 = 20 x 10, so n = 10
So, 20 x 10 less tickets will be sold for $1 x 10 = $10 increase in price.
Hence, the manager can increase the price of each ticket up to $10.
So, to sell at least 800 tickets, the maximum price of each ticket can be $60 + $10 = $70.
Hence, the value of p is p ≤ $70.
Solving Two-Step Inequalities Homework & Practice 4.7
Review & Refresh
Solve the inequality. Graph the solution.
Question 1.
-3x ≥ 18
Answer:
x ≤ -6
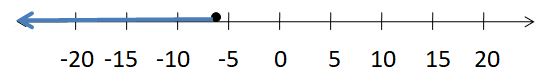
Explanation:
-3x ≥ 18
x ≤ -18/3
x ≤ -6
Question 2.
![]()
Answer:
d > 12

Explanation:
2/3 d > 8
2d > 8 x 3
2d > 24
d > 24/2
d > 12
Question 3.
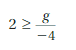
Answer:
-8 ≤ g
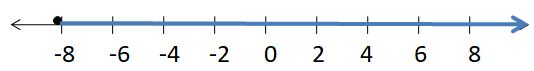
Explanation:
2 ≥ g/-4
2 x -4 ≤ g
-8 ≤ g
Find the missing values in the ratio table. Then write the equivalent ratios.
Question 4.

Answer:
Explanation:
12 = 4 x 3. So, 7x 3 = 21
7x 4 = 28. So, 4 x 4 = 16
Question 5.
Answer:
Explanation:
3 = 6 x 0.5. So, 10 x 0.5 = 5
50 = 10 x 5. So, 6 x 5 = 30
Question 6.
What is the volume of the cube?
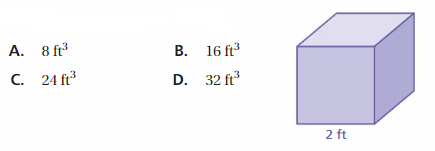
Answer:
A. 8 ft³
Explanation:
Cube volume formula = side³
Given side = 2 feet
Volume = 2³
= 2 x 2 x 2 = 8 ft³
Concepts, Skills, &Problem Solving
USING ALGEBRA TILES
Write the inequality modeled by the algebra tiles. Then solve the inequality using algebra tiles. Check your answer using properties of inequality. (See Exploration 1, p. 165.)
Question 7.
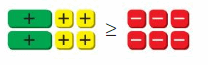
Answer:
x ≥ -5
Explanation:
x + 1 + 1 + x + 1 + 1 ≥ -1 – 1-1-1-1-1
2x + 4 ≥ -6
2x ≥ -6 – 4
2x ≥ -10
x ≥ -10/2
x ≥ -5
Question 8.

Answer:
x < -2
Explanation:
-x + 1 -x + 1 > +1 + 1+ 1+ 1+ 1+ 1
-2x + 2 > 6
-2x > 6 – 2
-2x > 4
x < -4/2
x < -2
SOLVING A TWO-STEP INEQUALITY
Solve the inequality. Graph the solution.
Question 9.
8y – 5 < 3
Answer:
y < 1

Explanation:
8y – 5 < 3
8y < 3 + 5
8y < 8
y < 1
Question 10.
3p + 2 ≥ -10
Answer:
p ≥ -4

Explanation:
3p + 2 ≥ -10
3p ≥ -10 – 2
3p ≥ -12
p ≥ -12/3
p ≥ -4
Question 11.
![]()
Answer:
-4.5 < h

Explanation:
2 – 8 > -4/3 h
-6 > -4/3 h
-6 x 3 > -4h
-18 > -4h
-18/-4 < h
-9/2 < h
-4.5 < h
Question 12.
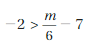
Answer:
30 > m

Explanation:
-2 + 7 > m/6
5 > m/6
5 x 6 > m
30 > m
Question 13.
-1.2b – 5.3 ≥ 1.9
Answer:
b ≤ -6
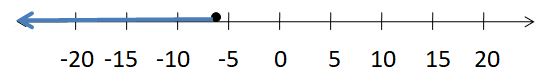
Explanation:
-1.2b ≥ 1.9 + 5.3
-1.2b ≥ 7.2
b ≤ -7.2/1.2
b ≤ -6
Question 14.
-1.3 ≥ 2.9 – 0.6r
Answer:
7 ≥ r

Explanation:
-1.3 ≥ 2.9 – 0.6r
-1.3 – 2.9 ≤ – 0.6r
-4.2 ≤ -0.6r
-4.2/-0.6 ≥ r
7 ≥ r
Question 15.
5(g + 4) > 15
Answer:
g > -1
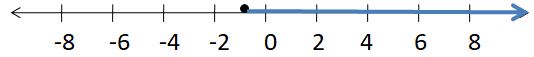
Explanation:
5(g + 4) > 15
(g + 4) > 15/5
(g + 4) > 3
g > 3 – 4
g > -1
Question 16.
4(w – 6) ≤ -12
Answer:
w ≤ 3
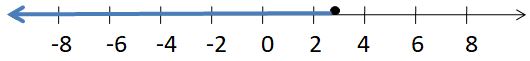
Explanation:
(w – 6) ≤ -12/4
(w – 6) ≤ -3
w ≤ -3 + 6
w ≤ 3
Question 17.
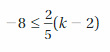
Answer:
-18 ≤ k

Explanation:
-8 x 5 ≤ 2(k – 2)
-40 / 2 ≤ k – 2
-20 ≤ k – 2
-20 + 2 ≤ k
-18 ≤ k
Question 18.
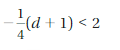
Answer:
d > -9

Explanation:
-1(d + 1) < 2 x 4
-1(d + 1) < 8
d + 1 > -8
d > -8 – 1
d > -9
Question 19.
7.2 > 0.9(n + 8.6)
Answer:
-0.6 > n

Explanation:
7.2/0.9 > (n + 8.6)
8 > (n + 8.6)
8 – 8.6 > n
-0.6 > n
Question 20.
20 ≥ -3.2(c – 4.3)
Answer:
-1.95 ≤ c

Explanation:
20 ≥ -3.2(c – 4.3)
20/-3.2 ≤ (c – 4.3)
-6.25 ≤ c – 4.3
-6.25 + 4.3 ≤ c
-1.95 ≤ c
YOU BE THE TEACHER
Your friend solves the inequality. Is your friend correct? Explain your reasoning.
Question 21.
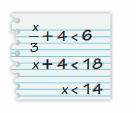
Answer:
Wrong
Explanation:
x/3+ 4 < 6
x/3 < 6 – 4
x/3 < 2
x < 2 x 6
x < 12
Question 22.
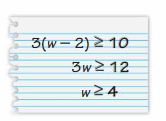
Answer:
Wrong
Explanation:
3(w – 2) ≥ 10
w – 2 ≥ 10/3
w ≥ 10/3 + 2
w ≥(10+6)/3
w ≥ 16/3
Question 23.
MODELING REAL LIFE
The first jump in a unicycle high-jump contest is shown. The bar is raised 2 centimeters after each jump. Solve the inequality 2n + 10 ≥ 26 to find the numbers of additional jumps needed to meet or exceed the goal of clearing a height of 26 centimeters.

Answer:
The numbers of additional jumps needed to meet or exceed the goal of clearing a height of 26 centimeters is 8.
Explanation:
2n + 10 ≥ 26
2n ≥ 26 – 10
2n ≥ 16
n ≥ 16/2
n ≥ 8
The numbers of additional jumps needed to meet or exceed the goal of clearing a height of 26 centimeters is 8.
SOLVING AN INEQUALITY
Solve the inequality. Graph the solution.
Question 24.
9x – 4x + 4 ≥ 36 – 12
Answer:
x ≥ 4
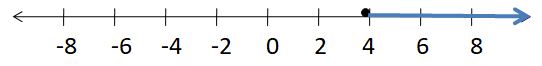
Explanation:
9x – 4x + 4 ≥ 36 – 12
5x + 4 ≥ 24
5x ≥ 24 – 4
5x ≥ 20
x ≥ 20/5
x ≥ 4
Question 25.
3d – 7d + 2.8 < 5.8 – 27
Answer:
d > -0.075

Explanation:
-4d + 2.8 < 3.1
-4d < 3.1 – 2.8
-4d < 0.3
d > -0.3/4
d > -0.075
Question 26.
MODELING REAL LIFE
A cave explorer is at an elevation of 38 feet. The explorer starts moving at a rate of 12 feet per minute. Write and solve an inequality that represents how long it will take the explorer to reach an elevation deeper than -200 feet.
Answer:
It takes 13 minutes 30 seconds for a cave explorer to reach an elevation deeper than -200 feet.
Explanation:
A cave explorer is at an elevation of 38 feet.
The explorer starts moving at a rate of 12 feet per minute.
He should reach an elevation deeper than -200 feet.
So, 38 + 12n ≤ 200
12n ≤ 200 – 38
12n ≤ 162
n ≤ 162/12
n ≤ 13.5
So, it takes 13 minutes 30 seconds for a cave explorer to reach an elevation deeper than -200 feet.
Question 27.
CRITICAL THINKING
A contestant in a weight-loss competition wants to lose an average of atleast 8 pounds per month during a five-month period. Based on the progress report, how many pounds must the contestant lose in the fifth month to meet the goal?
Answer:
6 pounds must the contestant lose in the fifth month to meet the goal
Explanation:
The total weight loss in five months = 12 + 9 + 5 + 8
= 34
A contestant in a weight-loss competition wants to lose an average of atleast 8 pounds per month during a five-month period.
So, he must loss at least 8 x 5 = 40 pounds on overall
Hence, he should lost 40 – 34 = 6 more pounds to meet the goal.
Question 28.
REASONING
A student theater charges $8.50 per ticket.
a. The theater has already sold 70 tickets. How many more tickets does the theater need to sell to earn atleast $750?
b. The theater increases the ticket price by $1. Without solving an inequality, describe how this aspects the total number of tickets needed to earn atleast $750. Explain your reasoning.
Answer:
a. 18 more tickets needed.
b. If the theater charges more per ticket, then they can sell fewer tickets to rach their goal $750.
Explanation:
a. Let t represent the number of additional tickets.
t + 70 is the total number of tickets sold.
Each ticket cost is $8.50, the theatre will earn a tota of $8.50(t + 70)
The theater wants to earn at least $750. So, 8.50(t + 70) ≥ 750
(t + 70) ≥ 750/8.50
t + 70 ≥ 88.23
(t) ≥ 88.23 – 70
t ≥ 18.235
So, 18 more tickets needed.
b. If the theater charges more per ticket, then they can sell fewer tickets to rach their goal $750.
Question 29.
DIG DEEPER!
A zoo does not have room to add any more tigers to an enclosure. According to regulations, the area of the enclosure must increase by 150 square feet for each tiger that is added. The zoo is able to enlarge the 450 square foot enclosure for a total area no greater than 1000 square feet. a. Write and solve an inequality that represents this situation. b. Describe the possible numbers of tigers that can be added to the enclosure. Explain your reasoning.

Answer:
(a + 150)t < 1000
Explanation:
Let us take the area of enclosure for a tiget as a.
The number of tigers as t
the area of the enclosure must increase by 150 square feet for each tiger that is added.
The zoo is able to enlarge the 450 square foot enclosure
(a + 150)t = 450
(a + 150)t < 1000
Question 30.
GEOMETRY
For what values of r will the area of the shaded region be greater than or equal to 12 square units?
Answer:
For r greater than equal to 8 the area of the shaded region be greater than or equal to 12 square units
Explanation:
Total area of rectangle = 3 x r = 3r
Area of unshaded triangle = 1/2 x r x 3 = 1.5r
The area of the shaded region = Total area of rectangle – Area of unshaded triangle
= 3r – 1.5r = 1.5r
The area of the shaded region be greater than or equal to 12 square units
1.5r ≥ 12
r ≥ 12/1.5
r ≥ 8
For r greater than equal to 8 the area of the shaded region be greater than or equal to 12 square units
Equations and Inequalities Connecting Concepts
Using the Problem-Solving Plan
Question 1.
Fencing costs $7 per foot. You install feet of the fencing along one side of a property, as shown. The property has an area of 15,750 square feet. What is the total cost of the fence?
Understand the problem.
You know the area, height, and one base length of the trapezoid-shaped property. You are asked to find the cost of x feet of fencing, given that the fencing costs $7 per foot.
Make a plan.
Use the formula for the area of a trapezoid to find the length of fencing that you buy. Then multiply the length of fencing by $7 to find the total cost.
Solve and check
Use the plan to solve the problem. Then check your solution.
Answer:
The total cost of the fence is $840.
Explanation:
The given image is in the shape of a trapezoid.
Traperzoid area formula = (a + b) xh/2
Here a = 90, b = x, h = 150
Area of property = (90 + x) x 150/2
= (90 + x) x 75
Given that, property area is 15,750 sq ft.
15750 = (90 + x)75
15750/75 = 90 + x
210 = 90 + x
210 – 90 = x
x = 120
Multiply x by fencing cost$7 to get total cost
Total cost = 120 x 7 = $840
Question 2.
A pool is in the shape of a rectangular prism with a length of 15 feet, a width of 10 feet, and a depth of 4 feet. The pool is filled with water at a rate no faster than 3 cubic feet per minute. How long does it take to fill the pool?
Answer:
The time is taken to fill the pool is more than 200 minutes.
Explanation:
Pool length = 15 ft, width = 10 ft, depth = 4 ft
Pool volume = length x width x depth
= 15 x 10 x 4 = 600 cubic feet
The water filled per minute is 3 cubic feet.
The time is taken to fill the pool = 600/3 = 200 minutes
Question 3.
The table shows your scores on 9 out of 10 quizzes that are each worth 20 points. What score do you need on the final quiz to have a mean score of atleast 17 points?

Answer:
You need to score 18 points
Explanation:
The total score on quiz = (15 + 14 + 16 + 19 + 18 + 19 + 20 + 15 + 16 + x)
= 152 + x
Mean of total score = (152 + x)/ 10
So, (152 + x)/ 10 ≥ 17
152 + x ≥ 17 x 10
152 + x ≥ 170
x ≥ 170 – 152
x ≥ 18
So, you need to score 18 points
Performance Task
Distance and Brightness of the Stars
At the beginning of this chapter, you watched a STEAM Video called “Space Cadets.” You are now ready to complete the performance task related to this video, available at BigIdeasMath.com. Be sure to use the problem-solving plan as you work through the performance task.

Equations and Inequalities Chapter Review
Review Vocabulary
Write the definition and give an example of each vocabulary term.
Graphic Organizers
You can use a Summary Triangle to explain a concept. Here is an example of Summary Triangle for Addition Property of Equality.

Choose and complete a graphic organizer to help you study the concept.
- equivalent equations
- Subtraction Property of Equality
- Multiplication Property of Equality
- Division Property of Equality
- graphing inequalities
- Addition and Subtraction Properties of Inequality
- Multiplication and Division Properties of Inequality

Chapter Self-Assessment
As you complete the exercises, use the scale below to rate your understanding of the success criteria in your journal.

4.1 Solving Equations Using Addition or Subtraction (pp. 127–132)
Solve the equation. Check your solution.
Question 1.
p – 3 = -4
Answer:
p = -1
Explanation:
p – 3 = -4
p = -4 + 3
p = -1
Putting p = -1 in p – 3 = -4
-1 – 3 = -4
Question 2.
6 + q = 1
Answer:
q = -5
Explanation:
6 + q = 1
q = 1 – 6
q = -5
Putting q = -5 in 6 + q = 1
6 + (-5) = 6 – 5 = 1
Question 3.
-2 + j = -22
Answer:
j = -20
Explanation:
-2 + j = -22
j = -22 + 2
j = -20
Putting j = -20 in -2 + j = -22
-2 + (-20) = -2 – 20 = -22
Question 4.
b – 19 = -11
Answer:
b = 8
Explanation:
b – 19 = -11
b = -11 + 19
b = 8
Putting b = 8 in b – 19 = -11
8 – 19 = -11
Question 5.
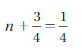
Answer:
n = -1/2
Explanation:
n + 3/4 = 1/4
n = 1/4 – 3/4
n = -2/4
n = -1/2
putting n = -1/2 in n + 3/4 = 1/4
-1/2 + 3/4 = (-2 + 3)/4 = 1/4
Question 6.
![]()
Answer:
v = -1/24
Explanation:
v – 5/6 = -7/8
v = -7/8 + 5/6
v = (-21 + 20)/24
v = -1/24
Putting v = -1/24 in v – 5/6 = -7/8
-1/24 – 5/6 = (-1 – 20)/24 = -21/24 = -7/8
Question 7.
t – 3.7 = 1.2
Answer:
t = 4.9
Explanation:
t = 1.2 + 3.7
t = 4.9
Putting t = 4.9 in t – 3.7 = 1.2
4.9 – 3.7 = 1.2
Question 8.
l + 15.2 = -4.5
Answer:
I = -19.7
Explanation:
l + 15.2 = -4.5
I = -4.5 – 15.2
I = -19.7
Putting I = -19.7 in l + 15.2 = -4.5
-19.7 + 15.2 = -4.5
Question 9.
Write the word sentence as an equation. Then solve the equation.
![]()
Answer:
5 + x = -4
x = -9
Explanation:
5 more than a number x is -4
5 + x = -4
x = -4 – 5
x = -9
Question 10.
The perimeter of the trapezoid-shaped window frame is 23.59 feet. Write and solve an equation to find the unknown side length (in feet).

Answer:
The unknown side length is 8.7 feet
Explanation:
Perimeter = 23.59
3.65 + 5.62 + 5.62 + x = 23.59
14.89 + x = 23.59
x = 23.59 – 14.89
x = 8.7
The unknown side length is 8.7 feet
Question 11.
You are 5 years older than your cousin. How old is your cousin when you are 12 years old? Justify your answer.
Answer:
Cousin age is 7 years when you are 12 years old.
Explanation:
My age = cousin + 5
When my age is 12 years
12 = cousin + 5
cousin = 12 – 5
cousin = 7 years
Cousin age is 7 years when you are 12 years old.
4.2 Solving Equations Using Multiplication or Division (pp. 133–138)
Solve the equation. Check your solution.
Question 12.
![]()
Answer:
x = -24
Explanation:
x = -8 x 3
x = -24
Putting x = -24 in x/3 = -8
-24/3 = -8
Question 13.
![]()
Answer:
y = -49
Explanation:
-7 = y/7
-7 x 7 = y
y = -49
Putting y = -49 in -7 = y/7
-7 = -49/7
Question 14.
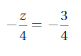
Answer:
z = 3
Explanation:
-z/4 = -3/4
z/4 = 3/4
z = (3/4) x 4
z = 3
Putting z = 3 in -z/4 = -3/4
-3/4 = -3/4
Question 15.
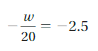
Answer:
w = 50
Explanation:
-w/20 = -2.5
w = 2.5 x 20
w = 50
Putting w = 50 in -w/20 = -2.5
-50/20 = -2.5
Question 16.
4x = -8
Answer:
x = -2
Explanation:
4x = -8
x = -8/4
x = -2
Putting x = -2 in 4x = -8
4(-2) = -8
Question 17.
-10 = 2y
Answer:
y = -5
Explanation:
-10 = 2y
y = -10/2
y = -5
Putting y = -5 in -10 = 2y
-10 = 2(-5)
Question 18.
-5.4z = -32.4
Answer:
z = 6
Explanation:
-5.4z = -32.4
z = 32.4/5.4
z = 6
Putting z = 6 in -5.4z = -32.4
-5.4(6) = -32.4
Question 19.
-6.8w = 3.4
Answer:
w = -0.5
Explanation:
-6.8w = 3.4
w = -3.4/6.8
w = -0.5
Putting w = -0.5 in -6.8w = 3.4
-6.8(-0.5) = 3.4
Question 20.
Write “3 times a number is 42” as an equation. Then solve the equation.
Answer:
x = 14
Explanation:
3 times a number is 42
3x = 42
x = 42/3
x = 14
Question 21.
The mean temperature change is -3.2°F per day for 5 days. Write and solve an equation to find the total change over the 5-day period.
Answer:
The total change in temperature for 5 days is -16°F.
Explanation:
The mean temperature change is -3.2°F per day
The total change in temperature for 5 days = 5 x -3.2 = -16°F
x= 5 x -3.2
x = -16°F
Question 22.
Describe a real-life situation that can be modeled by 7x = 1.75.
Answer:
x = 0.25
Explanation:
7x = 1.75.
x = 1.75/7
x = 0.25
4.3 Solving Two-Step Equations (pp. 139–144)
Solve the equation. Check your solution.
Question 23.
-2c + 6 = -8
Answer:
c = 2
Explanation:
-2c = -8 – 6
-2c = -14
c = 14/2
c = 7
Putting c = 7 in -2c + 6 = -8
-2(7) + 6 = -14 + 6 = -8
Question 24.
5 – 4t = 6
Answer:
t = -1/4
Explanation:
-4t = 6 – 5
-4t = 1
t = -1/4
Putting t = -1/4 in 5 – 4t = 6
5 – 4(-1/4) = 5 + 1 = 6
Question 25.
-3x – 4.6 = 5.9
Answer:
x = -3.5
Explanation:
-3x = 5.9 + 4.6
-3x = 10.5
x = -10.5/3
x = -3.5
Putting x = -3.5 in -3x – 4.6 = 5.9
-3(-3.5) – 4.6 = 10.5 – 4.6 = 5.9
Question 26.
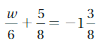
Answer:
w = -12
Explanation:
w/6 + 5/8 = -11/8
w/6 = -11/8 – 5/8
w/6 = -16/8
w/6 = -2
w = -2 x 6
w = -12
Putting w = -12 in w/6 + 5/8 = -11/8
-12/6 + 5/8 = -2 + 5/8
= (-16 + 5)/8 = -11/8
Question 27.
3(3w – 4) = -20
Answer:
w = -8/9
Explanation:
3(3w – 4) = -20
(3w – 4) = -20/3
3w = -20/3 + 4
3w = (-20 + 12)/3
3w = -8/3
w = -8/3 x 1/3
w = -8/9
Putting w = -8/9 in 3(3w – 4) = -20
3(3(-8/9) – 4) = 3(-8/3 – 4)
= 3(-8 – 12)/3 = -20
Question 28.
-6y + 8y = -24
Answer:
y = -12
Explanation:
2y = -24
y = -24/2
y = -12
putting y = -12 in -6y + 8y = -24
-6(-12) + 8(-12) = 72 – 96 = -24
Question 29.
The floor of a canyon has an elevation of -14.5 feet. Erosion causes the elevation to change by -1.5 feet per year. How many years will it take for the canyon floor to reach an elevation of 31 feet? Justify your solution.
Answer:
It takes 11 years for the canyon floor to reach an elevation of 31 feet
Explanation:
The floor of a canyon has an elevation of -14.5 feet
Erosion causes the elevation to change by -1.5 feet per year
Let us take x as the no of years take for the canyon floor to reach an elevation of 31 feet
-14.5 – 1.5x > 31
-1.5x > -31 + 14.5
-1.5x > -16.5
x < 16.5/1.5
x < 11
So, it take 11 years.
4.4 Writing and Graphing Inequalities (pp. 145–150)
Write the word sentence as an inequality.
Question 30.
A number w is greater than -3.
Answer:
w > -3
Explanation:
Greater than means >
w > -3
Question 31.
A number y minus \([\frac{1}{2}/latex] is no more than –[latex][\frac{3}{2}/latex].
Answer:
y – 1/2 < -3/2
Explanation:
No more than means <
y – 1/2 < -3/2
Tell whether the given value is a solution of the inequality.
Question 32.
5 + j > 8; j = 7
Answer:
j = 7 is the solution of the inequality.
Explanation:
5 + j > 8; j = 7
5 + 7 > 8
12 > 8
Question 33.
6 ÷ n ≤ -5; n = -3
Answer:
n = -3 is not the solution of the inequality.
Explanation:
6 ÷ n ≤ -5; n = -3
6 ÷ -3 ≤ -5
-2 ≤ -5
2 ≥ 5
Question 34.
7p ≥ p – 12; p = -2
Answer:
p = -2 is the solution of the inequality.
Explanation:
7p ≥ p – 12; p = -2
7(-2) ≥ -2 – 12
-14 ≥ -14
Graph the inequality on a number line.
Question 35.
q > -1.3
Answer:

Question 36.
![]()
Answer:
s < 7/4

Question 37.
The Enhanced Fujita scale rates the intensity of tornadoes based on wind speed and damage caused. An EF5 tornado is estimated to have wind speeds greater than 200 miles per hour. Write and graph an inequality that represents this situation.
Answer:
w > 200
Explanation:
The wind speed is greater than 200 miles per hour
w > 200
4.5 Solving Inequalities Using Addition or Subtraction (pp. 151–156)
Solve the inequality. Graph the solution.
Question 38.
d + 12 < 19
Answer:
d < 7
Explanation:
d + 12 < 19
d < 19 – 12
d < 7
Question 39.
t – 4 ≤ -14
Answer:
t ≤ -10
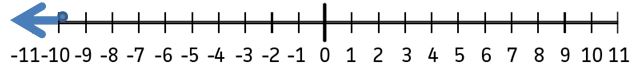
Explanation:
t – 4 ≤ -14
t – 4 + 4 ≤ -14 + 4
t ≤ -10
Question 40.
-8 ≤ z + 6.4
Answer:
-14.4 ≤ z
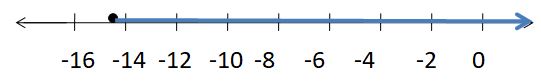
Explanation:
-8 ≤ z + 6.4
-8 -6.4 ≤ z + 6.4 -6.4
-14.4 ≤ z
Question 41.
A small cruise ship can hold up to 500 people. There are 115 crew members on board the ship.
a. Write and solve an inequality that represents the additional numbers of people that can board the ship.
b. Can 385 more people board the ship? Explain.
Answer:
a. 115 + x < 500
b. Yes
Explanation:
A small cruise ship can hold up to 500 people. There are 115 crew members on board the ship.
a. 115 + x < 500
b. a. 115 + x < 500
a. 115 + x – 115 < 500 -115
a < 385
Question 42.
Write an inequality that can be solved using the Subtraction Property of Inequality and has a solution of all numbers less than -3.
Answer:
x + 15 < 12
Explanation:
x + 15 < 12
x + 15 – 15 < 12 – 15
x < -3
4.6 Solving Inequalities Using Multiplication or Division (pp. 157–164)
Solve the inequality. Graph the solution.
Question 43.
6q < -18
Answer:
q < -3

Explanation:
6q < -18
6q/6 < -18/6
q < -3
Question 44.
![]()
Answer:
r ≥-18

Explanation:
-r/3 ≤ 6
-r ≤ 6 * 3
-r ≤ 18
r ≥-18
Question 45.
![]()
Answer:
3 < s

Explanation:
-4 x 3 > -4s
-12 > -4s
12 < 4s
12/4 < s
3 < s
Question 46.
Write the word sentence as an inequality. Then solve the inequality.
![]()
Answer:
p < -7
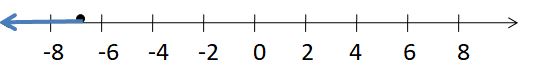
Explanation:
-3p > 21
-p > 21/3
-p > 7
p < -7
Question 47.
You are organizing books on a shelf. Each book has a width of [latex]\frac{3}{4}\) inch. Write and solve an inequality for the numbers of books b that can fit on the shelf.
Answer:
32 books will fit on the shelf.
Explanation:
Width of book = 3/4 inch
The total width of shelf = 24 in
3/4 b < 24
3b < 24 x 4
3b < 96
b < 96/3
b < 32
So, 32 books will fit on the shelf.
4.7 Solving Two-Step Inequalities (pp. 165–170)
Solve the inequality. Graph the solution.
Question 48.
3x + 4 > 16
Answer:
x > 4

Explanation:
3x + 4 > 16
3x + 4 – 4 > 16 – 4
3x > 12
x > 12/3
x > 4
Question 49.
![]()
Answer:
z ≥ -8

Explanation:
z / -2 ≤ -2 + 6
z/-2 ≤ 4
z ≥ 4 x -2
z ≥ -8
Question 50.
-2t – 5 < 9
Answer:
t > -7
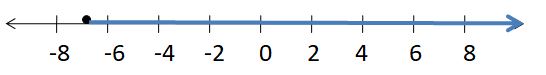
Explanation:
-2t – 5 + 5 < 9 + 5
-2t < 14
t > -14/2
t > -7
Question 51.
7(q + 2) < -77
Answer:
q < -13
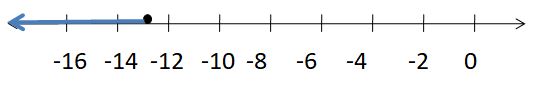
Explanation:
7(q + 2) < -77
q + 2 < -77/7
q + 2 < -11
q < -11 – 2
q < -13
Question 52.
![]()
Answer:
p ≥ -21
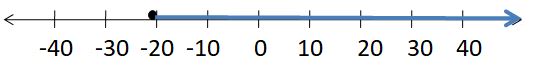
Explanation:
-1/3 (p + 9) ≤ 4
(p + 9) ≥ -4 x 3
p + 9 ≥ -12
p ≥ -12 – 9
p ≥ -21
Question 53.
1.2(j + 3.5) ≥ 4.8
Answer:
j ≥ 0.5

Explanation:
1.2(j + 3.5) ≥ 4.8
(j + 3.5) ≥ 4.8/1.2
(j + 3.5) ≥ 4
j ≥ 4 – 3.5
j ≥ 0.5
Question 54.
Your goal is to raise at least $50 in a charity fundraiser. You earn $3.50 for each candle sold. You also receive a $15 donation. Write and solve an inequality that represents the numbers of candles you must sell to reach your goal.
Answer:
You must sell 10 candles to reach your goal.
Explanation:
Your goal is to raise at least $50 in a charity fundraiser.
goal ≥ 50
You earn $3.50 for each candle sold. You also receive a $15 donation.
3.5x + 15 ≥ 50
3.5x ≥ 50 – 15
3.5x ≥ 35
x ≥ 35/3.5
x ≥ 10
Equations and Inequalities Practice Test
Solve the equation. Check your solution.
Question 1.
7x = -3
Answer:
x = -3/7
Explanation:
7x = -3
x = -3/7
Putting x = -3/7 in 7x = -3
7(-3/7) = -3
Question 2.
2(x + 1) = -2
Answer:
x = -2
Explanation:
2(x + 1) = -2
x + 1 = -2/2
x + 1 = -1
x = -1 – 1
x = -2
Putting x = -2 in 2(x + 1) = -2
2(-2 + 1) = 2(-1) = -2
Question 3.
![]()
Answer:
g = -36
Explanation:
(2/9)g = -8
2g = -8 x 9
2g = -72
g = -72/2
g = -36
Putting g = -36 in (2/9)g = -8
(2/9) x (-36) = 2 x -4 = -8
Question 4.
z + 14.5 = 5.4
Answer:
z = -9.2
Explanation:
z + 14.5 = 5.4
z = 5.4 – 14.5
z = -9.2
Putting z = -9.2 in z + 14.5 = 5.4
-9.2 + 14.5 = 5.4
Question 5.
-14 = c – 10
Answer:
Explanation:
-14 + 10 = c
c = -4
Putting c = -4 in -14 = c – 10
-14 = -4 – 10
Question 6.

Answer:
k = -7
Explanation:
(2/7)k – 3/8 = -19/8
(2/7)k = -19/8 + 3/8
(2/7)k = -16/8
(2/7)k = -2
2k = -2 x 7
2k = -14
k = -14/2
k = -7
Putting k = -7 in (2/7)k – 3/8 = -19/8
(2/7)(-7) – 3/8 = -2 – 3/8
= (-16 – 3)/8 = -19/8
Write the word sentence as an inequality.
Question 7.
A number k plus 19.5 is less than or equal to 40.
Answer:
k + 19.5 ≤ 40
Explanation:
A number k plus 19.5 is less than or equal to 40.
less than or equal to means ≤
k + 19.5 ≤ 40
Question 8.
A number q multiplied by \(\frac{1}{4}\) is greater than -16.
Answer:
q/4 > -16
Explanation:
A number q multiplied by 1/4 is greater than -16.
greater than means >
q (1/4) > -16
q/4 > -16
Tell whether the given value is a solution of the inequality.
Question 9.
n – 3 ≤ 4; n = 7
Answer:
The given value is the solution for the inequality.
Explanation:
Putting n = 7 in n – 3 ≤ 4
7 – 3 ≤ 4
4 ≤ 4
So, the given value is the solution for the inequality.
Question 10.
![]()
Answer:
The given value is not the solution for the inequality.
Explanation:
Putting m = -7 in (-3/7)m < 1 + m
(-3/7)(-7) < 1 + (-7)
3 < -6
So, the given value is not the solution for the inequality.
Solve the inequality. Graph the solution.
Question 11.
x – 4 > -6
Answer:
x > -2

Explanation:
x – 4 > -6
x > -6 + 4
x > -2
Question 12.
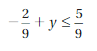
Answer:
y ≤ 7/9

Explanation:
-2/9 + y ≤ 5/9
y ≤ 5/9 + 2/9
y ≤ 7/9
Question 13.
-6z ≥ 36
Answer:
z ≥ -6

Explanation:
-6z ≥ 36
z ≥ -36/6
z ≥ -6
Question 14.
![]()
Answer:
-20.8 ≥ p
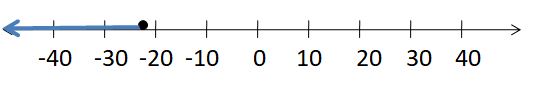
Explanation:
-5.2 ≥ p/4
-5.2 x 4 ≥ p
-20.8 ≥ p
Question 15.
4k – 8 ≥ 20
Answer:
k ≥ 7
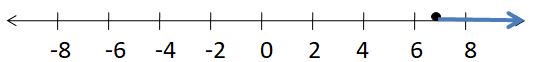
Explanation:
4k – 8 ≥ 20
4k ≥ 20 + 8
4k ≥ 28
k ≥ 28/4
k ≥ 7
Question 16.
-0.6 > -0.3(d + 6)
Answer:
-4 > d
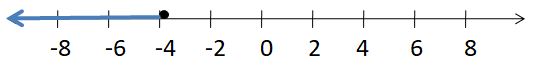
Explanation:
-0.6/(-0.3) > (d + 6)
2 > d + 6
2 – 6 > d
-4 > d
Question 17.
You lose 0.3 point for stepping out of bounds during a gymnastics floor routine. Your final score is 9.124. Write and solve an equation to find your score without the penalty.
Answer:
My score without penalty is 9.424
Explanation:
You lose 0.3 point for stepping out of bounds during a gymnastics floor routine.
Assume my score without penalty as x.
Your final score is 9.124.
x – 0.3 = 9.124
x = 9.124 + 0.3
x = 9.424
So, my score without penalty is 9.424
Question 18.
Half the area of the rectangle shown is 24 square inches. Write and solve an equation to find the value of x.
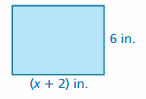
Answer:
x = 2
Explanation:
Rectangle area = length x breadth
6(x+ 2) = 24
(x + 2) = 24/6
x + 2 = 4
x = 4 – 2
x = 2
Question 19.
You can spend no more than $100 on a party you are hosting. The cost per guest is $8.
a. Write and solve an inequality that represents the numbers of guests you can invite to the party.
b. What is the greatest number of guests that you can invite to the party? Explain your reasoning.

Answer:
a. You can invite 12 guests to the party.
b. The greatest number of guests that you can invite to the party is 13.
Explanation:
You can spend no more than $100 on a party you are hosting. The cost per guest is $8.
a. 8x < 100
x < 100/8
x < 12.5
So, you can invite 12 guests to the party.
b. x < 12.5
So, the greatest number of guests that you can invite to the party is 13.
Question 20.
You have $30 to buy baseball cards. Each pack of cards costs $5. Write and solve an inequality that represents the numbers of packs of baseball cards you can buy and still have atleast $10 left.
Answer:
I can buy at least 4 packs of baseball cards
Explanation:
You have $30 to buy baseball cards. Each pack of cards costs $5.
I must have at least 10 left after shopping
So, 5x + 10 ≥ 30
5x ≥ 30 – 10
5x ≥ 20
x ≥ 20/5
x ≥ 4
So, I can buy at least 4 packs of baseball cards
Question 21.
The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
a. Write and solve three inequalities for the previous statement using the triangle shown.
b. What values for x make sense?

Answer:
a. 6.4 > x
b. The values of x can be less than 64.
Explanation:
The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
17 + 15 > 5x
32 > 5x
32/5 > x
6.4 > x
b. x can be less than 64.
Equations and Inequalities Cumulative Practice
Question 1.
Which equation represents the word sentence?


Answer:
B. b/0.3 = -10
Explanation:
The quotient of b and 0.3 means b/0.3
The quotient of b and 0.3 equal to negative 10.
So, b/0.3 = -10
Question 2.
What is the value of the expression?

Answer:
-3/8 x 2/5 = -3/20
Explanation:
-3/8 x 2/5 = (-3/4) x (1/5)
= (-3/20)
Question 3.
Which graph represents the inequality?
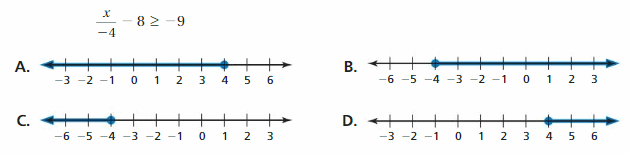
Answer:
A.
Explanation:
x/-4 – 8 ≥ -9
x/-4 ≥ -9 + 8
x/-4 ≥ -1
x ≤ -1 x -4
x ≤ 4
Question 4.
Which equation is equivalent to ![]()

Answer:
F.
Explanation:
-3/4 x + 1/8 = -3/8
-3/4 x =-3/8 – 1/8
Question 5.
What is the decimal form of 2\(\frac{5}{8}\) ?

Answer:
The decimal form of 2(5/8) is 2.25
Explanation:
The decimal form of 2(5/8)
= 18/8 = 2.25
Question 6.
What is the value of the expression when x = -5, y = 3, and z = -1?
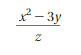
A. -34
B. -16
C. 16
D. 34
Answer:
B. -16
Explanation:
Putting x = -5, y = 3, and z = -1 in (x² – 3y)/z
= ((-5)² – 3(3))/(-1)
= (25 – 9)/(-1)
= -16
Question 7.
Which expression is equivalent to 9h – 6 + 7h – 5?
F. 3h + 2
G. 16h + 1
H. 2h – 1
I. 16h – 11
Answer:
I. 16h – 11
Explanation:
9h – 6 + 7h – 5 = 16h – 11
Question 8.
Your friend solved the equation -96 = -6(x – 15).
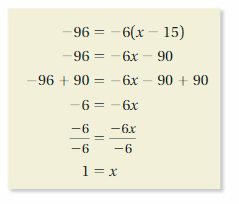
What should your friend do to correct her error?
A. First add 6 to both sides of the equation.
B. First subtract from both sides of the equation.
C. Distribute the -6 to get 6x – 90.
D. Distribute the -6 to get -6x + 90.
Answer:
D. Distribute the -6 to get -6x + 90.
Explanation:
-96 = -6(x – 15)
96 = 6(x – 15)
x – 15 = 96/6
x – 15 = 16
x = 16 + 15
x = 31
Question 9.
Which expression does not represent the perimeter of the rectangle?

F. 4j(60)
G. 8j + 120
H. 2(4j + 60)
I. 8(j + 15)
Answer:
F. 4j(60)
Explanation:
The perimeter of rectangle = 2(length + breadth)
= 2(4j + 60) = 8j + 120 = 8(j + 15)
Question 10.
What is the value of the expression?

Answer:
5/12 – 7/8 = -11/24
Explanation:
5/12 – 7/8 = (10 – 21)/24
= -11/24
Question 11.
You are selling T-shirts to raise money for a charity. You sell the T-shirts for $10 each.

Part A
You have already sold 2 T-shirts. How many more T-shirts must you sell to raise at least $500? Explain.
Part B
Your friend is raising money for the same charity and has not sold any T-shirts previously. He sells the T-shirts for $8 each. What are the total numbers of T-shirts he can sell to raise atleast $500? Explain.
Part C
Who has to sell more T-shirts in total? How many more? Explain.
Answer:
A. You need to sell 48 more t-shirts to raise at least $500
B. You need to sell more than 63 T-shirts to raise atleast $500
C. The person who is selling $8 per T-shirt has to sell more when compared with others.
Explanation:
The cost of each T-shirt = $10
A. You have already sold 2 T-shirts.
So, you earned = 2 x 10 = 20
The more number of T-shirts must you sell to raise at least $500
2 + 10x ≥ 500
10x ≥ 500 – 2
10x ≥ 488
x ≥ 488/10
x ≥ 48.8
B. The cost of each T-shirt = $8
The total numbers of T-shirts he can sell to raise atleast $500
8x ≥ 500
x ≥ 500/8
x ≥ 62.5
You need to sell more than 63 T-shirts to raise atleast $500
C. The person who is selling $8 per T-shirt has to sell more when compared with others.
Question 12.
Which expression has the same value as ![]()

Answer:
A. -1/3 + 1/9
Explanation:
Solve all the expressions and check which solution represents the given expression.
-2/3 – (-4/9) = -2/3 + 4/9
= (-6 + 4)/9
= -2/9
A. -1/3 + 1/9 = (-3 + 1)/9
= -2/9
B. -2/3 x (-13) = 2/9
As option A and given expression has the same solution. A is the answer.
Question 13.
You recycle (6c + 10) water bottles. Your friend recycles twice as many water bottles as you recycle. Which expression represents the amount of water bottles your friend recycles?
F. 3c + 5
G. 12c + 10
H. 12c + 20
I. 6c + 12
Answer:
H. 12c + 20
Explanation:
Friend recycles twice as many water bottles as you recycle.
You recycle (6c + 10) water bottles.
So, my friend recycles 2(6c + 10) = 12c + 20
Question 14.
What is the value of the expression?
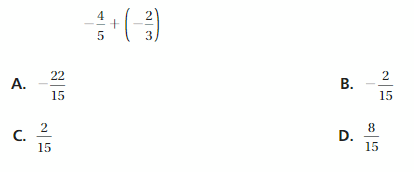
Answer:
-4/5 + (-2/3) = -22/15
Explanation:
-4/5 + (-2/3) = -4/5 – 2/3
= (-12 – 10)/15
= -22/15
Conclusion:
We are here to make your child master in maths. All the answers are explained in a detailed and simple manner. So, the students who are lagging in this topic can Download Big Ideas Math Answers Grade 7 Chapter 4 Equations and Inequalities. We do not charge any amount to download the pdf. Stay tuned to get the latest updates regarding the Big Ideas Math Grade 7 Answer Key for all the chapters.