Big Ideas Math Answers Grade 3 Chapter 6 Relate Area to Multiplication pdf is available here. We have provided the solutions to all the questions in the BIM 3rd Grade Chapter 6 Relate Area to Multiplication in the pdf format. This Big Ideas Math Answers Grade 3 Chapter 6 Relate Area to Multiplication helps you to complete the homework in time and also to enhance the knowledge. You can learn the concepts in depth.
Big Ideas Math Book 3rd Grade Answer Key Chapter 6 Relate Area to Multiplication
Check out the topics before you start your preparation. We have prepared the solutions for the entire chapter in an easy manner. The topics covered in this chapter are areas, measure area using standard units, etc. You can know how to use the formula for suitable problems from here. Hence make use of the below links and learn the fundamentals or basics from the primary level itself.
Lesson: 1 Understand Area
Lesson: 2 Measure Area Using Standard Units
- Lesson 6.2 Measure Area Using Standard Units
- Measure Area Using Standard Units Homework & Practice 6.2
Lesson: 3 Find Area by Multiplying
Lesson: 4 Area and the Distributive Property
- Lesson 6.4 Area and the Distributive Property
- Area and the Distributive Property Homework & Practice 6.4
Lesson: 5 Find Areas of More Shapes
Performance Task
- Relate Area to Multiplication Performance Task
- Relate Area to Multiplication Activity
- Relate Area to Multiplication Chapter Practice
Lesson 6.1 Understand Area
Explore and Grow
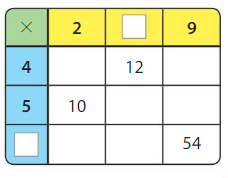
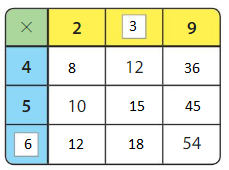
Try to cover the rectangle with the given number of color tiles.

How many color tiles do you need to completely cover the rectangle with no gaps or overlaps?
____ color tiles
Answer:
6 + 10 + 8 = 24 tiles are needed to cover the rectangle
Precision
Why is it important to line up the tiles side to side?
Think and Grow: Counting to Find Area
Answer:
It is important to line up tiles side to side with out gaps so that we can count tiles to find area of the shape.
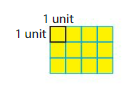
Area is the amount of surface a shape covers. The area of a unit square is 1 square unit.

12 unit squares cover the rectangle with no gaps or overlaps. So, the area of the rectangle is 12 square units.
Example
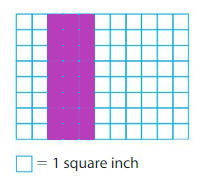
Find the area of the rectangle. Count the unit squares needed to cover the rectangle.
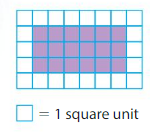

___ unit squares cover the rectangle.
So, the area is ___ square units.
Answer:
18 unit squares cover the rectangle.
So, the area is 18 square units.
Explanation:
There are 3 rows with 6 color tiles each in the grid
6+6+6=18.
18 unit squares cover the rectangle.
So, The area is 18 square units.
Show and Grow
Question 1.
Find the area of the shape.
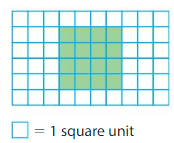
___ unit squares cover the shape.
So, the area is ___ square units.
Answer:
16 unit squares cover the shape.
So, the area is 16 square units.
Explanation:
There are 4 color tiles in row and there are 4 such rows of color tiles in the shape.
So, 4+4+4+4=16
Therefore 16 unit squares cover the shape.
So, the area is 16 square units.
Question 2.
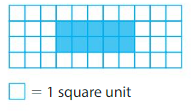
___ unit squares cover the shape.
So, the area is ___ square units.
Answer:
10 unit squares cover the shape.
So, the area is 10 square units.
Explanation:
There are 5 color tiles in a row and there are 2 such rows in the shape.
So, 5×2=10
Therefore
10 unit squares cover the shape.
So, The area is 10 unit squares.
Apply and Grow: Practice
Find the area of the shape.
Question 3.
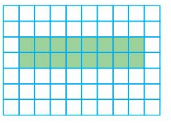
___ unit squares cover the shape.
So, the area is ___ square units.
Answer:
16 unit squares cover the shape.
So, the area is 16 square units.
Explanation:
So, There are 8 color tiles in a row and there are 2 such rows in the shape.
8×2=16
Therefore 16 unit squares cover the shape.
So, the area is 16 unit squares.
Question 4.
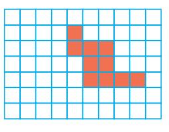
Area = ___ square units.
Answer:
Area =10 square units.
Explanation:
In the above grid there are 10 color boxes.
So, the area of the given shape is 10 square units.
Question 5.
Area = ___ square units.
Answer:
Area = 11 square units.
Explanation:
In the above grid there are 11 color boxes
so, the area of the shape is 11 square units.
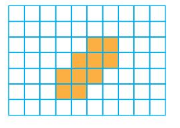
Question 6.

Area = ___ square units.
Answer:
Area =18 square units.
Explanation:
There are 2 color boxes in first row and there are 4 color boxes in the following 4 rows.
So, 2+4+4+4+4=18
Therefore the area of the shape is 18 square units.
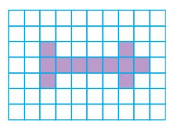
Question 7.
Area = square units.
Answer:
Area = 10 square units.
Explanation:
In the above grid there are 2 color boxes in the first row ,last row and 3 color boxes each in middle two rows.
So,2+3+3+2=10
Therefore the area of the shape is 10 square units.
Question 8.
YOU BE THE TEACHER
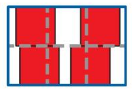
Newton uses 4 color tiles to cover the rectangle. He says the area is 4 square units. Is he correct? Explain.
Answer:
No, Newton is not correct. To find the area of the shape using tiles they must be arranged side by side without any gaps or overlaps. In the above picture there are gaps between the color tiles.
Question 9.
Open-Ended
Draw a shape that has an area of 16 square units

Answer:
Think and Grow: Modeling Real Life
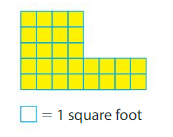
Part of a zoo map is shown. What is the area of the lion exhibit?
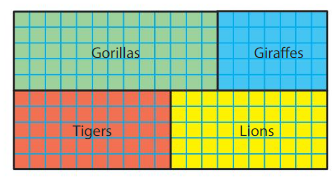
The lion exhibit is ___ square units.
Answer:
The lion exhibit is 50 square units.
Explanation:
In the above zoo map the area of lion exhibit is represented using yellow colored tiles.
There are 10 yellow colored tiles in a row and there are 5 such rows of yellow color tiles.
So,10×5=50
Therefore the area of the lion exhibit in the zoo is 50 square units.
Show and Grow
Use the field day map to answer the question.
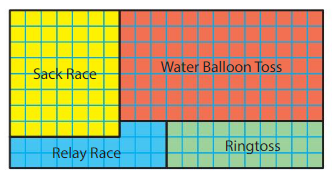
Question 10.
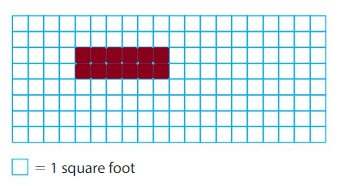
What is the area of the relay race section?
Answer:
Area of Relay Race section is 23 square units.
Explanation:
In the above field day map Relay Race section is represented using blue colored tiles.
There are 3 tiles in first row and 10 tiles in the following two rows.
So,3+10+10=23
Therefore the area of the Relay Race section is 23 square units.
Question 11.
Which area is greater, the ring toss section or the relay race section? Explain.
Answer:
The ring toss section is greater than relay race section.
Explanation:
The area of ring toss section is 30 square units and the area of the relay race section is 23 square units.so the ring toss section is greater than relay race section.
Understand Area Homework & practice 6.1
Find the area of the shape.
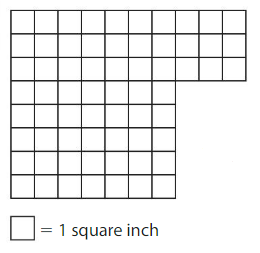
Question 1.
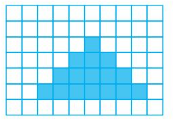
___ unit squares cover the shape.
So, the area is ___ square units.
Answer:
18 unit squares cover the shape.
So, the area is 18 square units.
Explanation:
In the above grid there is 1 blue color tile in first row followed by 3 tiles in the next,5 tiles in the later and 9 tiles at the end.
So,1+3+5+9=18
18 color tiles cover the area.
Therefore the area of the given shape is 18 square units.
Question 2.
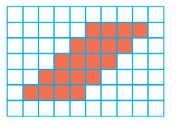
Area = ___ square units.
Answer:
Area = 20 square units.
Explanation:
In the above grid there are 4 red colored tiles in a row and there are 5 such rows.
So,4×5=20
20 tiles cover the shape.
Therefore the area of the given shape is 20 square units.
Question 3.
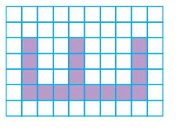
Area = ___ square units.
Answer:
Area = 17 square units.
Explanation:
In the above grid there are 17 purple colored tiles.
Therefore the area of the given shape is 17 square units.
Question 4.
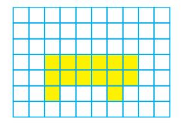
Area = ___ square units.
Answer:
Area = 14 square units.
Explanation:
There are 6 yellow colored tiles in 2 rows each followed by 2 more tiles in the third row.
So,6+6+2=14
14 tiles cover the shape.
Therefore the area of the shape is 14 square units.
Question 5.
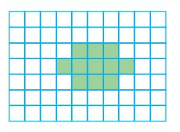
Area = ___ square units.
Answer:
Area = 11 square units.
Explanation:
There are 3 green colored boxes in the first and third row of the above shape and 5 boxes in the middle row.
So,3+5+3=11
11 color tiles cover the shape.
Therefore the area of the shape is 11 square units.
Question 6.

Area = ___ square units.
Answer:
Area =12 square units.
Explanation:
There are 6 color tiles each in two rows.
So,6+6=12
12 color tiles cover the shape
Therefore the area of the shape is 12 square units.
Question 7.
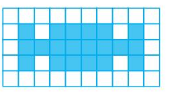
Area = ___ square units.
Answer:
Area = 20 square units.
Explanation:
There are 20 color tiles in the above grid.
So, the area of the shape is 20 square units.
Question 8.
Your friend says each shape has an area of 8 square units. Is your friend correct? Explain.
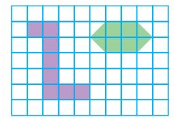
Answer:
My friend is incorrect.
Explanation:
One of the shape in in the above grid has gaps.
Modeling Real Life
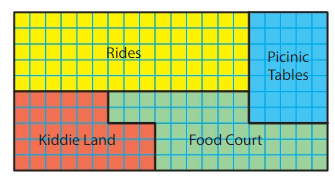
Use the amusement park map to answer the question.
Answer:
Question 9.
What is the area of the food court section?
Answer:
The area of the food court is 51 square units.
Explanation:
There are 9 green tiles in first 2 rows each and 11 green tiles in the following 3 rows.
So,9+9+11+11+11=51
51 green tiles cover the food court area
Therefore the area of the food court is 51 square units.
Question 10.
Which area is greater, the kiddie land section or the picnic tables section? Explain.
Answer:
Area of kiddie land section is greater than area of picnic tables.
Explanation:
The kiddie land section is covered with 39 color tiles and the picnic tables section is covered with 35 color tiles.
Review & Refresh
Find the quotient.
Question 11.
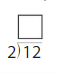
Answer:6
Explanation:(2×6=12)
Question 12

Answer:4
Explanation:(7×4=28)
Question 13.

Answer:9
Explanation:(6×9=54)
Question 14.
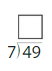
Answer:7
Explanation:(7×7=49)
Lesson 6.2 Measure Area Using Standard Units
Explore and Grow
Use the colored squares.
How many blue squares do you think it will take to cover the rectangle?
___ blue squares
How many red squares do you think it will take to cover the rectangle?

Answer:
Find the area of the rectangle using the blue squares.
Area = ___ blue square units
Find the area of the rectangle using the red squares.
Area = ___ red square units
Answer:
Reasoning
Why is the number of blue squares needed to cover the rectangle different from the number of red squares needed?
Answer:
The number of blue squares needed to cover the rectangle is different from the number of red squares as sizes of the squares are different.
Think and Grow: Measuring Area Using Standard Units
You can measure area using different standard units. Here are some standard units of length and area.
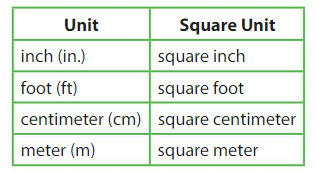
Unit squares can represent different standard units.

Each side is 1 unit. The area is 1 square unit.

Each Side represents 1 inch. The area is 1 square inch.
Example
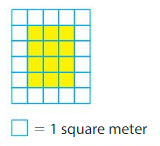
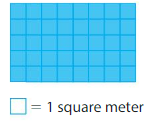
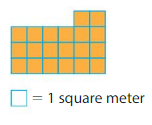
Find the area of the rectangle
___ unit squares cover the rectangle.
Each unit square represents
___________________
So, the area is _____
Answer:
In the above grid there are 3 yellow colored tiles in a row and there are 4 such rows.
So,3×4=12
12 unit squares cover the rectangle.
Each unit square represents 1 square meter.
So, the area is 12 square meters.
Show and Grow
Question 1.
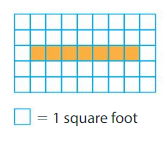
Find the area of the shape.
___ unit squares cover the rectangle.
Each unit square represents
________
So, the area is ____
Answer:
In the above grid there are 7 color tiles.
7 unit squares cover the rectangle.
Each unit square represents 1 square foot.
So, the area is 7 square feet.
Apply and Grow: Practice
Find the area of the shape.
Question 2.
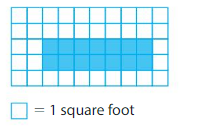
Area = ____
Answer:
There are 14 color tiles in the above grid.
14 unit squares cover the rectangle.
Each unit square represents 1 square foot.
So, the area is 14 square feet.
Question 3.
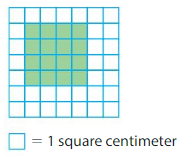
Area = ___
Answer:
There are 16 color tiles in the above grid.
16 unit squares cover the area.
Each unit square represents 1 square centimeter.
So, the area is 16 square centimeters.
Question 4.
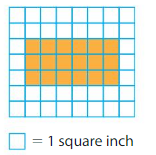
Area = ____
Answer:
There are 18 color tiles in the grid
18 square units cover the rectangle.
Each unit square represents 1 square inch.
So, the area is 18 square inches.
Question 5.
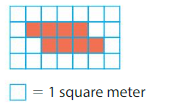
Area = ___
Answer:
There are 8 color boxes in the above grid.
8 unit squares cover the shape.
Each unit square represents 1 square meter.
So, the area is 8 square meters.
Question 6.
Number Sense
Which rectangle has an area of 12 square inches?
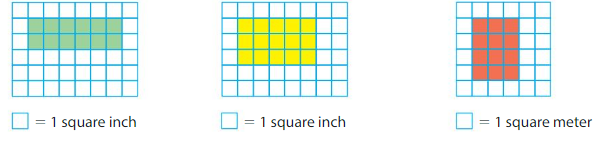
Answer:
In the above grid the green rectangle has 12 colored tiles, Yellow rectangle has 15 colored tiles and the orange rectangle also has 12 colored tiles but the unit square representation of orange rectangle is square meter. As green rectangle unit square representation is square inch, Green colored rectangle has the area of 12 square inches.
Question 7.
Reasoning
Is the area of a blanket more likely to be 30 square feet or 30 square centimeters? Explain.

Answer:
Centimeter is the smaller when compared to feet. usually we have blankets in bigger size so that a person fits in to it.
Therefore the area of the blanket will more likely be 30 square feet.
Think and Grow: Modeling Real Life
Whose puzzle has a greater area?
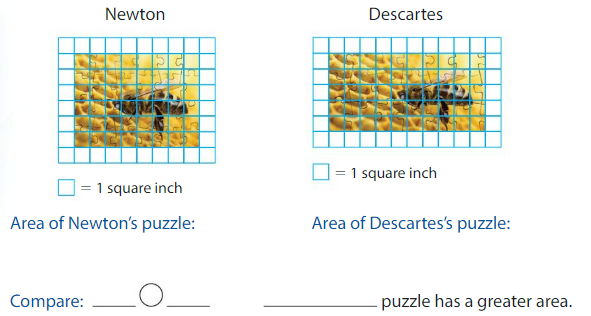
Answer:
Newton’s puzzle is covered with 48 tiles and Descartes puzzle is covered with 40 tiles.
Area of Newton’s puzzle is 48 square inches and area of Descartes’s puzzle is 40 square inches.
48>40.
Therefore Newton’s puzzle has the greater area.
Show and Grow
Question 8.
Compare the area of Newton’s puzzle shown above to the area of your friend’s puzzle. Whose puzzle has a greater area?
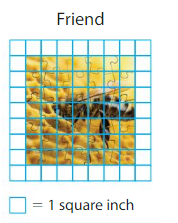
Answer:
In the above given puzzle there are 49 colored tiles .
The area of my friend’s puzzle is 49 square inches.
The area of Newton’s puzzle is 48 square inches.
48<49
Therefore Area of my friend’s puzzle is greater.
Question 9.
You want to weave a rectangular rug that has an area of 12 square feet. Draw and shade a rectangle to represent the rug.

Answer:
Measure Area Using Standard Units Homework & Practice 6.2
Find the area of the shape.
Question 1.
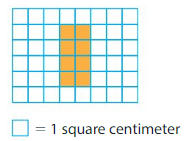
Answer:
Area = 8 square centimeters
Explanation:
There are 8 colored unit squares in the rectangle.
Each unit square represents 1 square centimeter.
So, area is 8 square centimeters.
Question 2.
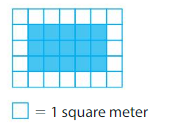
Area = ___
Answer:
Area = 15 square meters
Explanation:
There are 15 colored unit squares in the above rectangle.
Each unit square represents 1 square meter.
So, area is 15 square meters.
Question 3.
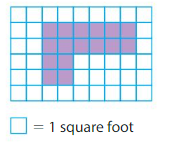
Area = ___
Answer:
Area = 16 square feet
Explanation:
There are 16 color unit squares in the above grid.
Each unit square represents 1 square foot.
So, area of the shape is 16 square feet.
Question 4.
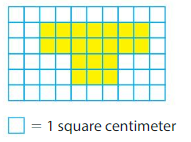
Area = ___
Answer:
Area = 20 square centimeters
Explanation:
There are 20 colored unit squares in above grid.
Each unit square represents 1 square centimeter.
So, area of the shape is 20 square centimeters.
Question 5.
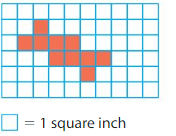
Area = ___
Answer:
Area = 10 square inches
Explanation:
There are 10 colored unit squares in the above grid.
Each unit square represents 1 square inch.
So, area of the shape is 10 square inches.
Question 6.
Precision
Your friend says the area of the shape is 13. What is wrong with her answer?
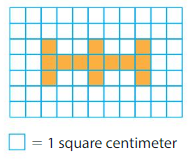
Answer:
My friend’s answer wrong as he/she didn’t mention the units of the area.
There are 13 color unit squares in the above grid.
Each unit square represents 1 square centimeter.
Therefore area is 13 square centimeters.
Question 7.
Number Sense
Find the area of the shape.
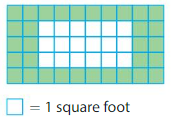
Answer:
Area = 32 square feet
Explanation:
In the above grid there are 32 color unit squares.
Each unit square represents 1 square foot.
Therefore area of the given shape is 32 square feet.
Question 8.
Modeling Real Life
Compare the areas of your bookmark and your friend’s bookmark. Whose bookmark has a greater area?
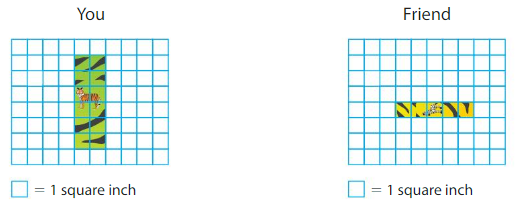
Answer:
My book mark has 12 colored unit squares and my friend’s book mark has 5 colored unit squares.
So area of my book mark is 12 square inches and my friend’s book mark is 5 square inches.
12>5
So, area of my book mark is greater.
Review & Refresh
Question 9.
Find the product of 4 × 5.
Number of jumps: ___
Size of jumps: ___

4 × 5 = ___
Answer:
Number of jumps =4
Size of jumps=5
4×5=20.
Lesson 6.3 Find Area by Multiplying
Explore and Grow
Write an equation for the array.
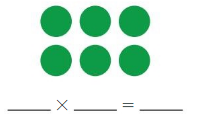
Answer: 2×3=6
Cover the rectangle with color tiles. Find the area of the rectangle.

Answer:
Structure
How can you use an array to find the area of rectangle?
Answer:
We can count the number of unit squares in a row and number of unit squares in a column and note them in the form of an array.
The answer of the equation will be the area of the rectangle.
Think and Grow: Find Area by Multiplying
Example
Find the area of the rectangle.

One Way:
Count the unit squares to find the area.
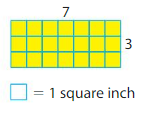
There are ___ unit squares
Another Way:
Think of the rectangle as an array.
Then use repeated addition or multiplication to find the area.
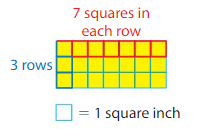
3 rows of ____ unit squares
7 + 7 + 7 = ____
3 × 7 = _____
So, the area is _____.
Show and Grow
Question 1.
Find the area of the rectangle.
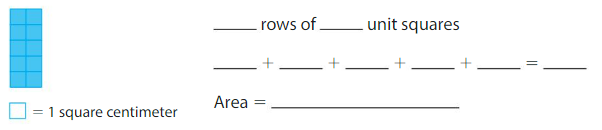
Answer:
There are 5 rows of 2 unit squares in each row.
So, 5 rows of 2 unit squares
2+2+2+2+2=10
Area=10 unit squares
Question 2.
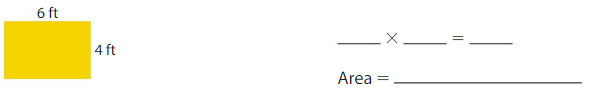
Answer:
6ft×4ft=24ft
Area =24 square feet.
Apply and Grow: Practice
Find the area of the rectangle
Question 3.
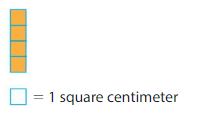
____ × _____ = ____
Area = _____
Answer:
There are 4 rows of 1 unit square in each row.so,
4×1=4
Area=4 square centimeter.
Question 4.
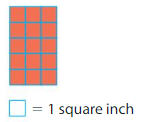
____ × _____ = ____
Area = _____
Answer:
There are 5 rows with 3 unit squares in each roe.so,
5×3=15
Area =15 square inches.
Question 5.
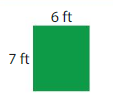
___ × ____ = ____
Area = _____
Answer:
7ft×6ft=42ft
Area=42 square feet
Question 6.
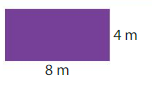
____ × _____ = ____
Area = ______
Answer:
8m×4m=32m
Area=32 square meters.
Question 7.
Open-Ended
Draw and label two different rectangles that each have an area of 12 square meters.
Answer:
Question 8.
DIG DEEPER!
Explain how to find the area of the rectangle.
Answer:
We can find area of the given rectangle by counting the number of square units in a row and in a column and multiplication of both is the area of the rectangle.
Think and Grow: Modeling Real Life
Space Poster Your rectangular animal poster is 4 feet long and 1 foot wide. Which poster has a greater area, your animal poster or your space poster?

Understand the problem:
Make a plan:
Solve:
Area of my animal poster is
4ft×1ft=4 square feet.
Area of my space poster is
3ft×2ft=6 square feet.
4<6
So, my space poster has a greater area.
Show and Grow
Question 9.
Descartes’s rectangular tablet is 10 inches long and 7 inches wide. Whose tablet has a greater area, Newton’s tablet or Descartes’s?
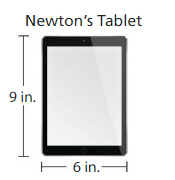
Answer:
Area of Newton’s table is
9in.×6in.=54 square inches.
Area of Descartes’s table is
10in.×7in.=70 square inches.
54<70
Therefore Descartes’s table has greater area.
Question 10.
Your friend paints a rectangular tile that is 8 inches long and 4 inches wide. You paint a square tile that is 6 inches long. Whose tile has a greater area?
Answer:
Area of rectangular tile is
8in.×4in.=32 square inches.
Area of square tile is
6in.×6in.=36 square inches.
32<36
So, square tile has greater area.
Question 11.
DIG DEEPER!
A sign has an area of 18 square feet. The sign is 6 feet long. How wide is the sign?
Answer:
There is a sign with an area of 18 square feet and length of 6 feet.
We have to find width of sign
Area=length ×width
18=6×width Or 6×width=18
Calculate and check 6 table 6×1=6,6×2=12,6×3=18
Therefore width of the sign is 3 feet.
Find Area by Multiplying Homework & Practice 6.3
Find the area of the rectangle
Question 1.
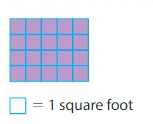
____ × ____ = ____
Area = _____
Answer:
There are 4 rows with 4 unit squares in each row.
4×4=16
Area =16 square feet.
Question 2.

____ × _____ = _____
Area = _____
Answer:
There are 3 rows with 8 unit squares in each row.
3×8=24
Area=24 square centimeters.
Question 3.

____ × _____ = _____
Area = _____
Answer:
6 in.×2 in.=12
Area=12 square inches.
Question 4.
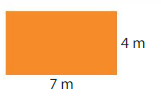
____ × _____ = _____
Area = _____
Answer:
7 m×4 m=28
Area=28 square meters.
Question 5.
DIG DEEPER!
Find the missing side length.

Answer:
Given Area of rectangle =30 square centimeters
Length =10 square meters
We have to find the length of the other side called breadth or width
Area= length ×width
30=10×width or 10×width=30
Count 10 table10×1=10,10×2=20,10×3=30
Therefore width or the length of the other side is 3 square meters.
Question 6.
YOU BE THE TEACHER
Descartes says he only needs the length of one side of a square to find the area. Is he correct? Explain.
Answer:
Yes he is correct. A square has sides with equal lengths on all sides.so length of one side is sufficient to measure the area of a square.
Question 7.
Modeling Real Life
A picture of your friend is 6 inches long and 4 inches wide. Which picture has a greater area, the picture of your friend or the picture of your pets?
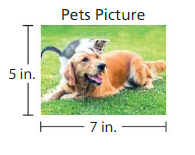
Answer:
Area of my friend’s picture is
6 in.×4 in.=24 square inches.
Area of my pets picture is
7 in.×5 in.=35 square inches.
24<35
Therefore pets picture has greater area.
Question 8.
DIG DEEPER!
A city street parking spot has an area of 72 square feet. The parking spot is 9 feet long. How wide is the parking spot?
Answer:
The city street parking spot has an area of 72 square feet. The length of the parking spot is 9 feet
We have to find the width of the parking spot.
Area =length × breadth
72=9×width or 9×width=72
So 9×1=9,9×2=18,———9×8=72
Therefore Width of the parking spot is 8 feet.
Review & Refresh
Use the Distributive Property to fill in the blanks
Question 9.
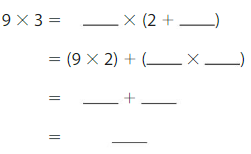
Answer:
9×3= 9×(2+1)
= (9×2)+(9×1)
= 18+9
= 27
Question 10.
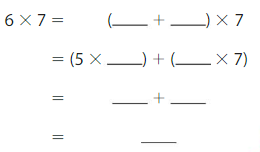
Answer:
6×7 = (5+1)×7
= (5×7)+(1×7)
= 35+7
= 42
Lesson 6.4 Area and the Distributive Property
Explore and Grow
Find the area of the rectangle two different ways.
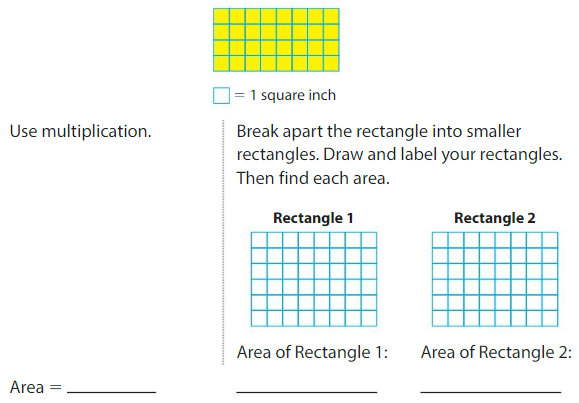
Structure
How does the area of the large rectangle compare to the areas of the smaller rectangles? What property does this show?
Answer:
The area of larger rectangle is divided in two smaller rectangles so the sum of the areas of smaller rectangles will be equal to area of larger rectangle.
Think and Grow: Area and the Distributive Property
You can use the Distributive Property to find the area of a rectangle. First, break apart the large rectangle into smaller rectangles. Then find the sum of the areas of the smaller rectangles.

Example
Use the Distributive Property to find the area of the rectangle.
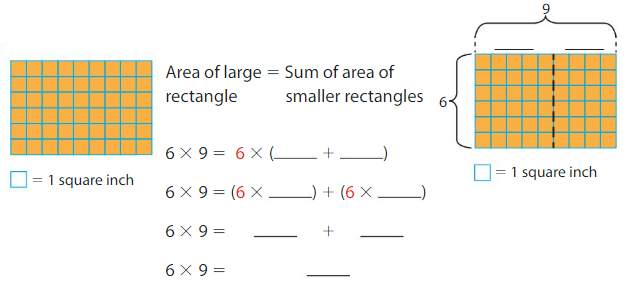
So, the area is _____.
Show and Grow
The area of large rectangle=sum of area of smaller rectangles
In the above grid there are 6 rows and 9 columns in the larger rectangle and this rectangle is divided into two smaller rectangles with 5 and 4 columns each.
Therefore
6×9=6×(5+4)
6×9=(6×5)+(6×4)
6×9=30+24
6×9=54
So, the area is 54 square inches.
Question 1.
Use the Distributive Property to find the area of the rectangle.
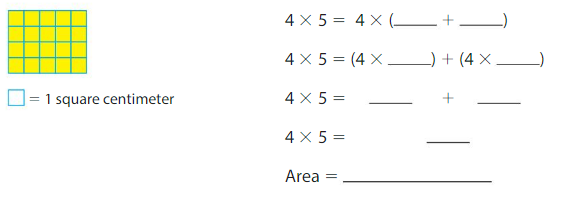
Answer:
In the above rectangle there are 4 rows and 5 columns. This is divided into smaller rectangles with 3 and 2 columns each.
Therefore
4×5=4×(3+2)
4×5=(4×3)+(4×2)
4×5=12+8
4×5=20
Area=20 square centimeters.
Apply and Grow: Practice
Use the Distributive Property to find the area of the rectangle.
Question 2.
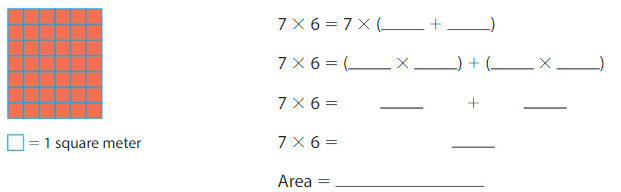
Answer:
There are 6 columns in the above large rectangle so the columns of smaller rectangles are 4 and
2 columns each.
Therefore
7×6=7×(4+2)
7×6=(7×4)+(7×2)
7×6=28+14
7×6=42
Area=42 square meters.
Question 3.
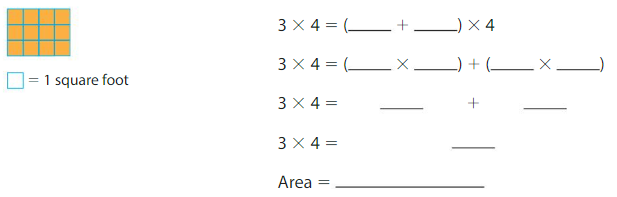
Answer:
Here we divide the rectangle using rows.
There are 3 rows in the above rectangle. so, the rows of the smaller rectangles are 2 and 1 each.
3×4=(2+1)×4
3×4=(2×4)+(1×4)
3×4=8+4
3×4=12
Area=12 square feet
Question 4.
Structure
Which equation represents the area of the rectangle?
5 × 7 = 5 × (6 + 1) = (5 × 6) + (5 × 1)
5 × 8 = 5 × (6 + 2) = (5 × 6) + (5 × 2)
5 × 7 = 5 × (2 + 5) = (5 × 2) + (5 × 5)
Answer:
Form the above grid we can understand that the large rectangle has 7 columns is divided into two smaller rectangles with 2 and 5 columns each. Therefore the 3rd equation represents the area of the rectangle.
Question 5.
DIG DEEPER!Explain how to use the Distributive Property to find the area of the rectangle.

Explanation:
To find the area of the rectangle using distributive property we have to divide the length of the rectangle into two and make two small rectangles.
Think and Grow: Modeling Real Life
Descartes cuts 1 rectangular piece of construction paper into2 rectangles. One rectangle is 8 inches wide and 10 inches long. The other rectangle is 8 inches wide and2 inches long. What were the dimensions and total area of the paper before it was cut?

Draw a picture:
Multiplication equation:
Distributive Property:
The piece of paper was _____ inches wide and ____ inches long before it was cut.
The total area of the piece of paper was _____ square inches.
Show and Grow
Question 6.
You cut 1 rectangular piece of fabric into 2 rectangles. One rectangle is 3 feet wide and 6 feet long. The other rectangle is3 feet wide and 9 feet long. What were the dimensions and total area of the fabric before it was cut?
Answer:
The piece of paper was 3 feet wide and 15 long before it was cut.
The total area of the piece of paper was 45 square feets.
Area of rectangle 1: 3×6=18 square feet
Area of rectangle 2: 3×9=27 square feet.
Area of paper is area of rectangle 1+2=18+27=45 square feet
Area and the Distributive Property Homework & Practice 6.4
Use the Distributive Property to find the area of the rectangle.
Question 1.
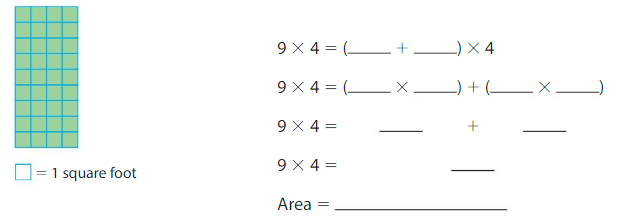
Answer:
In the above large rectangle there are 9 rows so, using Distributive Property we will find the area of large rectangle by dividing it into two smaller rectangles of 5 and 4 rows each.
9×4=(5+4)×4
9×4=(5×4)+(4×4)
9×4=20+16
9×4=36
Therefore Area=36 square feet.
Question 2.
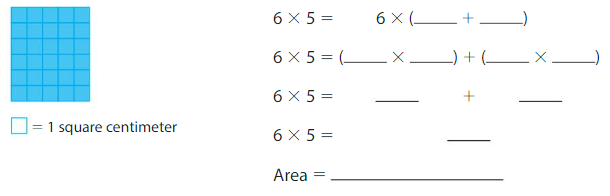
Answer:
In the above large rectangle there are 5 columns so, using Distributive Property we will find the area of the large rectangle by dividing it into two smaller rectangles of 3 and 2 columns each.
6×5=6×(3+2)
6×5=(6×3)+(6×2)
6×5=18+12
6×5=30
Area=30 square centimeters.
Structure
Draw rectangle for the expression
Question 3.
6 × (4 + 5)
Answer:
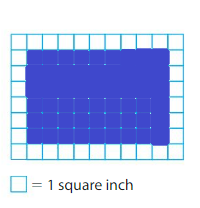
6x(4+5)= (6×4)+(6×5)
=24+30
=54.
Question 4.
(7 + 1) × 3
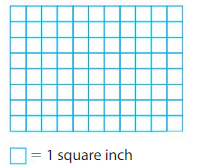
Answer:
(7+1)x3=(7×3)+(1×3)
= 21+3
=24
Question 5.
Which One Doesn’t Belong?
Which is not a way to break apart the rectangle?
5 × (4 + 4)
5 × (4 + 1)
(4 + 1) × 8
(2 + 3) × 8
Answer:
5×(4+1) is not a way to break apart the given rectangle as the columns given in the rectangle are 8 and the equation shows only 5 columns.
Question 6.
Modeling Real Life
You cut a rectangular piece of wrapping paper into2 rectangles. One rectangle is 10 inches wide and 6 inches long. The other rectangle is 10 inches wide and 5 inches long. What werethe dimensions and the total area of the wrapping paper before it was cut?

Answer:
As we know that the area of the larger rectangle is the sum of the areas of the smaller rectangles. So the areas of 2 rectangles are
Rectangle 1: 10 in. ×6 in.=60 square inches.
Rectangle 2: 10 in. ×5 in.=50 square inches.
Therefore Total Area=110(60+50) square inches.
Review & Refresh
Write the fact family for the numbers.
Question 7.
3, 8, 24
___ × ____ = _____
___ × ____ = _____
___ ÷ ____ = _____
___ ÷ ____ = _____
Answer:
Fact family of the numbers 3,8,24 is given below.
3×8=24
8×3=42
24÷3=8
24÷8=3
Question 8.
4, 9, 36
___ × ____ = _____
___ × ____ = _____
___ ÷ ____ = _____
___ ÷ ____ = _____
Answer:
Fact family of the numbers 4,9,36 is given below.
4×9=36
9×4=36
36÷4=9
36÷9=4
Question 8.
2, 7, 14
___ × ____ = _____
___ × ____ = _____
___ ÷ ____ = _____
___ ÷ ____ = _____
Answer:
Fact family of the numbers 2,7,14 is given below.
2×7=14
7×2=14
14÷2=7
14÷7=2
Lesson 6.5 Find Areas of More Shapes
Explore and Grow
Break apart the shape into two rectangles. Color each rectangle a different color. Find the area of each rectangle. Then find the total area of the shape.
Areas of Rectangles
Rectangle 1: _____ × ____ = _____ square inches
Rectangle 2: _____ × ____ = ______ square inches
Total Area of Shape: ____ + ____ = ____ square inches
Answer:
We have broken the shape into two rectangles
Rectangle 1:3×10=30 square inches
Rectangle 2: 5×7 =35 square inches
Total Area of Shape: 30+35=75 square inches.
Reasoning
Break apart the shape into two different rectangles and find the total area. What do you notice? Why is this true?
Answer:
When we broke apart the shape into two rectangles we noticed that the counting of rows and columns or units squares became possible. yes it is right to break the shape to find the area.
Think and Grow: Find Areas of More Shapes
Example
Find the area of the shape
One Way:
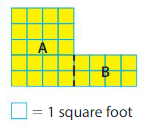
Areas of Rectangles
Rectangle A: 5 × 4 = _____ square feet
Rectangle B: 2 × 4 = ______ square feet
Area of Shape: ____ + ____ = ____ square feet
Another Way:
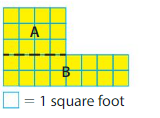
Areas of Rectangles
Rectangle A: 3 × 4 = _____ square feet
Rectangle B: 2 × 8 = ______ square feet
Area of Shape: ____ + ____ = ____ square feet
Answer:
Areas of Rectangles
Rectangle A:3×4=12 square feet
Rectangle B:2×8=16 square feet
Area of the shape:12+16=28 square feet.
Show and Grow
Question 1.
Find the area of the shape
Areas of Rectangles
Rectangle A: _____ × ____ = _____ square meters
Rectangle B: _____ × ____ = ______ square meters
Area of Shape: ____ + ____ = ____ square meters
Answer:
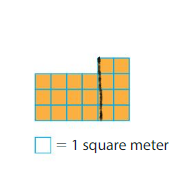
Rectangle A:3×4=12 square meters
Rectangle B:4×2=8 square meters
Area of shape:12+8=20 square meters.
Apply and Grow: Practice
Find the area of the shape
Question 2.
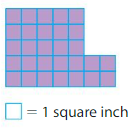
Areas of Rectangle A: _____ × ____ = _____ square inches
Areas of Rectangle B: _____ × ____ = ______ square inches
Area of Shape: ____ + ____ = ____ square inches
Answer:
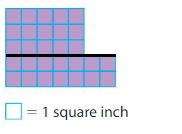
Divide the shape into two rectangles as 1st rectangle with 3 rows and 5 columns 2nd rectangle with 2 rows and 7 columns
Area of Rectangle A:3×5=15 square inches
Area of Rectangle B:2×7=14 square inches
Area of shape:15+14=29 square inches.
Question 3.
Area = _____
Answer:
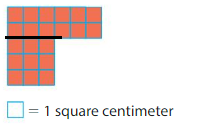
Divide the shape into two rectangles as 1st rectangle with 2 rows and 6 columns 2nd rectangle with 3 rows and 3 columns
Area of Rectangle 1: 2×6=12 square centimeters
Area of Rectangle 2: 3×3=9 square centimeters
Area of shape: 12+9=21 square centimeters.
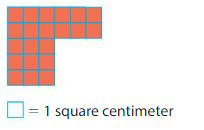
Question 4.
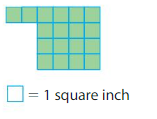
Area = ____
Answer:
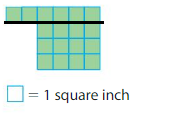
Divide the shape into two rectangles as 1st rectangle with 1 row and 6 columns 2nd rectangle with 3 rows and 4 columns
Area of Rectangle 1: 1×6=6 square inches
Area of Rectangle 2: 3×4=12 square inches
Area of shape: 6+12=18 square inches.
Question 5.
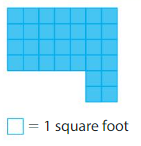
Area = ____
Answer:
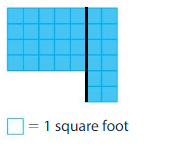
Divide the shape into two rectangles as 1st rectangle with 4 rows and 5 columns 2nd rectangle with 6 rows and 2 columns
Area Of Rectangle 1:4×5=20 square feet
Area of Rectangle 2:6×2=12 square feet
Area of shape : 20+12=32 square feet.
Question 6.

Area = _____
Answer:
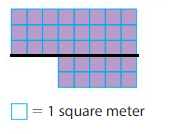
Divide the shape into two rectangles as 1st rectangle with 3 rows and 8 columns 2nd rectangle with 2 rows and 5 columns
Area of Rectangle 1:3×8=24 square meters
Area of Rectangle 2:2×5=10 square meters
Area of shape:24+10=34 square meters.
Question 7.
YOU BE THE ANSWER
Your friend says there is only one way to break apart the shape. Is your friend correct? Explain.
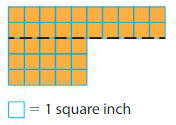
Answer:
No my friend is correct if we break the shape in any other way we will not get 2 rectangles.we may get 1 square and 1 rectangle.
Question 8.
DIG DEEPER!
Newton uses square tiles to make the design. Each tile is 2 inches long. What is the area of the design? Explain.

Answer:
Given: Each tile is 2 inches long and tile is square shape
Therefore area of each square tile is 2×2=4 square inches.
In the above shape we have 4 tiles
So, Area of shape = 4 × (area of tile) = 4 ×4=16 square inches.
Area=16 square inches.
Think and Grow: Modeling Real Life
What is the area of the balcony?
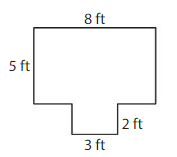
Answer:
The area of the balcony is 46 square feet
Explanation:
Area of Rectangle A:5×8=40 square feet , Area of Rectangle B:3×2=6 square feet
Area of the balcony:46 square feet
Show and Grow
Find the area of the miniature golf hole.
Question 9.
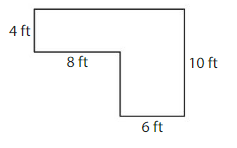
Answer:
Area of Rectangle A:4×(8+6)=4×(14)=56 square feet
Area of Rectangle B:6×(10-4)=6×6=36 square feet
Area of the golf hole:56+36=92 square feet
Question 10.
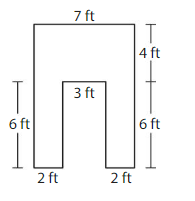
Answer:
Area=52 square feet
Explanation:
To find area here we need to calculate the total area and subtract the middle area from it. Total shape Length =6+4=10 , width =2+3+2=7 , Area of total shape =10×7=70 square feet, Part to be subtracted length =3 ,width =6
Area =3×6=18 square feet
Therefore area of the shape =Total area-area of part to be subtracted
=70‐18=52 square feet.
Question 11.
DIG DEEPER!
The floors of the classroom and closet have an area of 98 square meters. What is the area of the closet floor? Explain
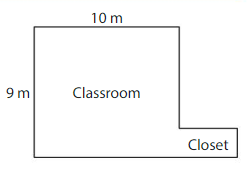
Answer:
Area of closets =8 square meters.
Explanation:
Given here that total area is 98 square meters. As shown in the figure above area of class room is 9×10=90 square meters.
Therefore Area of closets = Total area – Area of class room
=98-90=8
Area of closets =8 square meters.
Find Areas of More Shapes Homework & Practice 6.5
Find the area of the shape
Question 1.
Areas of Rectangle A: _____ × ____ = _____ square feet
Areas of Rectangle B: _____ × ____ = ______ square feet
Area of Shape: ____ + ____ = ____ square feet
Answer:
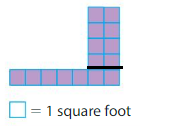
Area of Rectangle A:4×2=8 square feet
Area of Rectangle B:=1×7=7 square feet
Area of shape:=8+7=15 square feet.
Question 2.
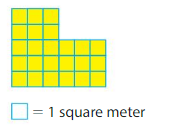
Area = ____
Answer:
Area of Rectangle A: 2×3=6 square meters
Area of Rectangle B: 3×6=18 square meters
Area of shape: 6+18=24 square meters.
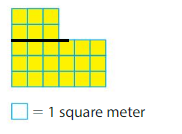
Question 3.
Area = _____
Answer:
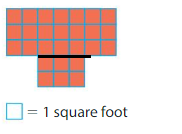
Area of Rectangle A: 3×7=21 square feet
Area of Rectangle B: 2×3=6 square feet
Area of shape: 21+6=27 square feet.
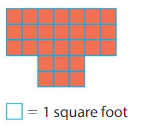
Question 4.
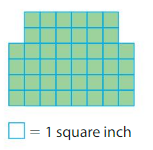
Area = _____
Answer:
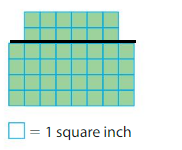
Area of Rectangle A:2×6=12 square inches.
Area of Rectangle B:4×8=36 square inches.
Area of shape :12+36=48 square inches.
Question 5.

Area = _____
Answer:
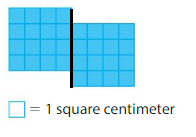
Area of square A:4×4=16 square centimeters
Area of square B:4×4=16 square centimeters
Area of shape:16+16=32 square centimeters.
Question 6.
Number Sense
Newton makes a design with squares. What is the total area of his design?
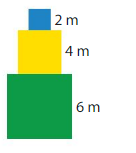
Answer:
Area of blue square is 2×2=4 square meters
Area of yellow square is 4×4=16 square meters
Area of green square is 6×6=36 square meters
Therefore Area of shape=4+16+36=56 square meters
Question 7.
Precision
A landscaper sketches a design for a yard.How much greater is the area of the grass than the area of the rocks?
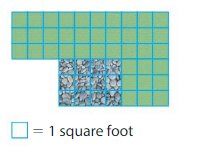
Answer:
Area of rock is 3×4=12 square feet.
To find area of the grass we divide it into 2 rectangles with 3 rows, 7 columns and 6 rows and 3 columns.
Area=(3×7)+(7×6) =21+42=63.
Area of grass- area of rock=63‐12=51.
So, area of grass is 53 square feet more than area of rock.
Question 8.Modeling Real Life
What is the area of the counter top?
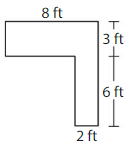
Answer:
Divide the shape into 2 parts
1:8ft×3ft=24 square feet
2:6ft×2ft=12 square feet
Area of counter top = 21+12=33 square feet.
Question 9.
DIG DEEPER!
The floors of the barn stall and feeding area havean area of 22 square meters. What is the area of the barn stall floor? Explain.
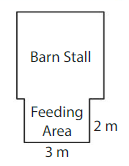
Answer:
The total area of bran stall and feeding areas 22 square meters. Feeding area =3×2=6 square meters
The area of only barn stall floor =Total area ‐feeding area
=22‐6 = 16 square meters
Therefore area of barn stall floor is 16 square meters.
Review & Refresh
Complete the table.
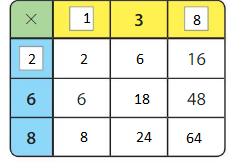
Question 10.
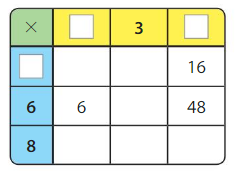
Answer:
Relate Area to Multiplication Performance Task
Question 1.
The map shows the top view of an obstacle course.
a. What is the area of the net?
b. What is the area of the hopscotch track?
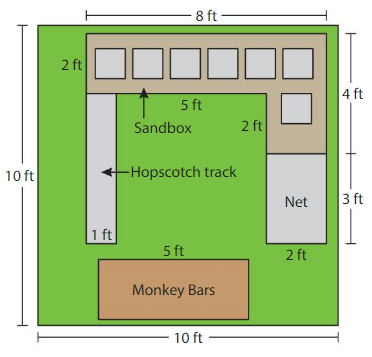
c. The area of the mud pit under the monkey bars is 10 square feet. What is the missing side length of the mud pit?
d. Each stepping-stone in the sandbox covers 1 square foot. What not is the area of the sandbox not covered with stones?
e. What is the area of just the grass?
Answer:
a.
Area of net=length ×width =3×2=6 square feet
Therefore area of net =6 square feet
b.
To find area of hopscotch track we have to find length of the track.
Total length of obstacle course is 10 ft
Length below the hopscotch= total length-length of sand box and net ie 10-4+3=3
Length above the hopscotch is 2 ft
Therefore Length of hopscotch =total length- length above and below the track=10-(2+3)=5ft
So, area of hopscotch course =5ft×1ft=5 square feet.
c.
Area of mud pit under the monkeys bars is 10 square feet.
Length of monkeys bars is 5ft
Length of the other side of monkeys bars is total area divided by length
Width of other side=10÷5=2
Therefore length of other side of mud pit is 2 feet.
d.
The total area of sand box is
8×2=16 square feet + 2×2=4 square feet
Area=20 square feet
As given in the question each sandbox covers 1 square foot of area.
As there are 7 sandboxes area of sandboxes is 7 square feet.
Therefore area of sandbox not covered with stones is 20-7 = 13 square feet.
e.
The area of just grass is the total area subtracted with area of all courses .
Total area=10×10= 100 square feet.
Area of net=6 square feet, Area of hopscotch =5 square feet, Area of monkeys bar=10 square feet, Area of sandbox = 20 square feet
Area of just grass= 100‐(6+5+10+20)=100‐41
Therefore area of just grass=59 square feet.
Question 2.
The obstacle course opens at 1 o’clock. It is half past 12. How many more minutes until the course opens?
Answer:
1 hour = 60 minutes, Half past 12 indicates 12:30
As Obstacle course opens at 1 o’ clock so, There are 30 more minutes until the course open.
Relate Area to Multiplication Activity
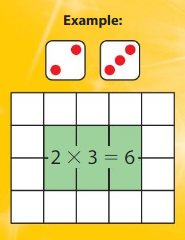
Area Roll and Conquer
Directions:
- Players take turns rolling two dice.
- On your turn, create a rectangle with the numbers on the dice as the side lengths. Your rectangle cannot cover another rectangle.
- Shade the rectangle in your color. Record the multiplication equation for the rectangle.
- If you cannot create a rectangle on the board, then you lose your turn. Play 10 rounds, if possible.
- The player with the greatest area covered wins!

Answer:
Relate Area to Multiplication Chapter Practice
6.1 Understand Area
Find the area of the shape.
Question 1.
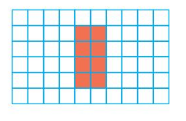
Area = ___ square units
Answer:
In the above grid there are 8 color tiles.
1 tile is equal to 1 square unit.
So, area =8 square units.
Question 2.
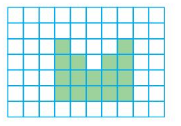
Area = ___ square units
Answer:
In the above grid there are 15 color tiles.
1 tile is equal to 1 square unit.
So, area =15 square units.
6.2 Measure Area Using Standard Units
Find the area of the shape.
Question 3.
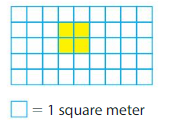
Area = ___
Answer:
In the above grid there are 4 colored unit squares.
1 unit represents 1 square meter.
Therefore Area=4 square meters.
Question 4.
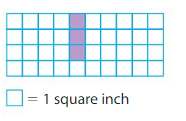
Area = ___
Answer:
In the above grid there are 3 colored unit squares.
1 unit square represents 1 square inch.
Therefore Area=3 square inches.
Question 5.
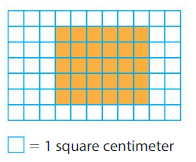
Area = ___
Answer:
In the above grid there are 30 colored unit squares.
1 unit square represents 1 square centimeter.
Therefore Area=30 square centimeters.
Question 6.
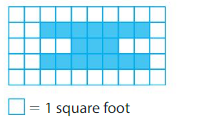
Area = ___
Answer:
In the above grid there are 16 colored unit squares.
1 unit square represents 1 square foot.
Therefore Area=16 square feet.
6.3 Find Area by Multiplying
Question 7.
Find the area of the rectangle.
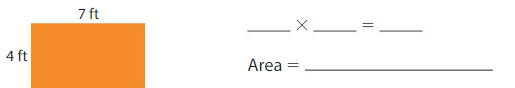
Answer:
The above rectangle is 7ft long and 4 feet wide
So area of the rectangle is length ×breadth
7ft×4ft=28 square feet.
Therefore Area=28 square feet.
Question 8.
Modeling Real Life
A textbook cover has an area of 80 square inches. The cover is 8 inches wide. How long is the cover?

Answer:
Area of the book is 80 square inches and width is 8 inches, We have to find the length of the book
Area=length × width
So, 80=length ×8 or 8×length=80 square inches
Count 8 table: 8×1=8,8×2=16,——8×10=80.
Therefore Length f the book is 10 inches.
6.4 Area and the Distributive Property
Question 9.
Use the Distributive Property to find the area of the rectangle.
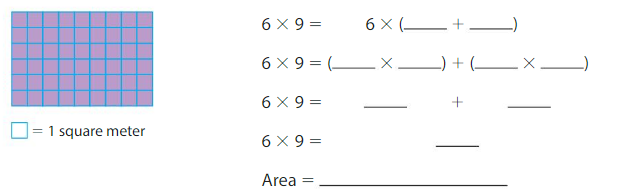
Answer:
The above rectangle has 9 columns and to find the area of rectangle using Distributive property this is divided into two smaller rectangles with 6 and 3 columns each.
6×9=6×(6+3)
6×9=(6×6)+(6×3)
6×9=36+18
6×9=54
Area=54 square meters.
6.5 Find Area of More Shapes
Question 10.
Find the area of the shape.
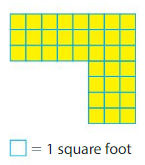
Area=________
Answer:
To find the area of the shape we can divide the shape into two rectangles. Rectangle A:3 rows and 8 columns Rectangle B:4 rows and 3 columns
Area of rectangle A:3×8=24 square feet
Area of rectangle B:4×3=12 square feet
Therefore area of shape:24+12=35 square feet.
Conclusion:
The Solution Key of Big Ideas Math Grade 3 Chapter 6 Relate Area to Multiplication helps the teachers and parents to explain the problems to the children. Feel free to clarify your doubts by posting the comments in the below box. Keep in touch with our ccssmath answers to get the solutions of all grade 3 chapters.