A quadrilateral can be defined as a closed geometric, two-dimensional shape having 4 straight sides. It has 4 vertices and angles. The types of quadrilaterals are parallelograms, squares, rhombus, and rectangle. The sum of all interior angles of a quadrilateral is equal to 360°. The angle is formed when two line segments meet at a common point. The angle can be measured in degrees or radians. The angles of a quadrilateral are the angles formed inside the closed shape.
Sum of Angles of a Quadrilateral Theorem & Proof
The sum of interior angles of a quadrilateral is 360 degrees.
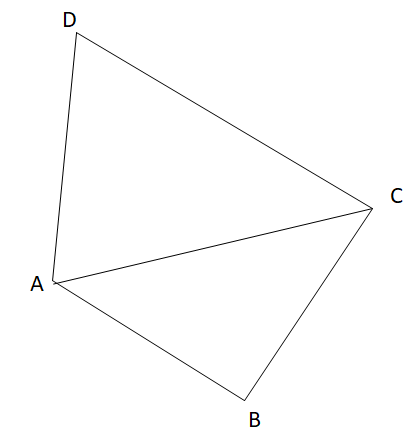
In the quadrilateral ABCD
∠ABC, ∠ADC, ∠DCB, ∠CBA are the interior angles
AC is the diagonal of the quadrilateral
AC splits the quadrilateral into two triangles ∆ABC and ∆ADC
We know that sum of angles of a quadrilateral is 360°
So, ∠ABC + ∠ADC + ∠DCB + ∠CBA = 360°
Let’s prove that sum of all interior angles of a quadrilateral is 360 degrees.
We know that the sum of angles in a triangle is 180°
In triangle ADC
∠CAD + ∠DCA + ∠D = 180° —- (i)
In the triangle ABC
∠B + ∠BAC + ∠BCA = 180° —- (ii)
Add both the equations
∠CAD + ∠DCA + ∠D + ∠B + ∠BAC + ∠BCA = 180° + 180°
∠D + (∠CAD + ∠BAC) + (∠BCA + ∠DCA) + ∠B = 360°
We can see that ∠CAD + ∠BAC = ∠DAB, ∠BCA + ∠DCA = ∠BCD
So, ∠D + ∠DAB + ∠BCD + ∠B = 360°
∠D + ∠A + ∠C + ∠B = 360°
Therefore, the sum of angles of a quadrilateral is 360°
Quadrilateral Angles Sum Propoerty
Each quadrilateral has 4 angles. The sum of its interior angles is always 360 degrees. So, we can find the angles of the quadrilateral if we know the remaining 3 angles or 2 angles or 1 angle and 4 sides. For a square or rectangle, the value of all angles is 90 degrees.
Also, Read
- What is a Quadrilateral?
- Construct Different Types of Quadrilaterals
- Different Types of Quadrilaterals
Examples on Quadrilateral Angles
Example 1:
Find the fourth angle of the quadrilateral if three angles are 85°, 100°, 60°?
Solution:
The given three angles of a quadrilateral are 85°, 100°, 60°
We know that the sum of angles of a quadrilateral is 360°
So, ∠A + ∠B + ∠C + ∠D = 360°
85° + 100° + 60° + x° = 360
245° + x° = 360°
x° = 360° – 245°
x° = 115°
Therefore, the fourth angle of the quadrilateral is 115°.
Example 2:
Find the measure of the missing angles in a parallelogram if ∠A = 75°?
Solution:
We know that the opposite angles of a parallelogram are equal.
So, ∠C = ∠A, ∠B = ∠D
Sum of angles is 360°
∠A + ∠B + ∠C + ∠D = 360°
75° + ∠B + 75° + ∠D = 360°
150° + ∠B + ∠D = 360°
∠B + ∠D = 360° – 150°
∠B + ∠D = 210°
∠B + ∠B = 210°
2∠B = 210°
∠B = \(\frac { 210° }{ 2 } \)
∠B = 105°
So, other angles of a parallelogram are 105°, 75°, 105°.
Example 3:
The angle of a quadrilateral are (3x + 2)°, (x – 3)°, (2x + 1)°, 2(2x + 5)° respectively. Find the value of x and the measure of each angle?
Solution:
The given angles are ∠A = (3x + 2)°, ∠B = (x – 3)°, ∠C = (2x + 1)°, ∠D = 2(2x + 5)°
We know that the sum of angles of a quadrilateral is 360°
∠A + ∠B + ∠C + ∠D = 360°
(3x + 2)° + (x – 3)° + (2x + 1)° + 2(2x + 5)° = 360°
3x + 2 + x – 3 + 2x + 1 + 4x + 10 = 360
10x + 10 = 360
10x = 360 – 10
10x = 350
x = \(\frac { 350 }{ 10 } \)
x = 35
The measurement of each angle of a quadrilateral is ∠A = (3x + 2)° = (3(35) + 2) = 105 + 2 = 107°
∠B = (x – 3)° = (35 – 3) = 32°
∠C = (2x + 1)° = (2(35) + 1) = 70 + 1 = 71°
∠D = 2(2x + 5)° = 2(2(35) + 5) = 2(70 + 5) = 2(75) = 150°
Example 4:
The three angles of a closed 4 sided geometric figure are 20.87°, 53.11°, 8.57°. Find the fourth angle?
Solution:
The given angles are ∠A = 20.87°, ∠B = 53.11°, ∠C = 8.57°
We know that the sum of angles of a quadrilateral is 360°
∠A + ∠B + ∠C + ∠D = 360°
20.87° + 53.11° + 8.57° + x° = 360°
82.55° + x° = 360°
x = 360 – 82.55
x = 277.45°
Therefore, the fourth angle of the closed 3 sided geometric figure is 277.45°.
FAQs on Sum of Angles of a Quadrilateral
1. What is the sum of the internal angles of a quadrilateral?
The sum of angles of a quadrilateral is 360 degrees.
2. What are the properties of a quadrilateral?
The three different properties of a quadrilateral are it has four sides, four vertices, four angles. And it is a closed 2-dimensional geometric figure. The sum of within angles is 360 degrees.
3. How do you prove the angle sum property of a quadrilateral?
To prove the sum property of a quadrilateral, draw a diagonal to divide it into two triangles. The sum of all interior angles of a triangle is 180 degrees. thus, the sum of angles of a quadrilateral becomes 360°.
4. What is the sum of all interior angles of a pentagon?
Draw one diagonal that should divide the pentagon into one triangle, one quadrilateral. The sum of angles of a triangle is 180 degrees, the sum of angles of a quadrilateral is 360 degrees. So, the sum of all interior angles of a pentagon is 180 + 360 = 540°.
