Eureka Math Grade 7 Module 4 End of Module Assessment Answer Key

Engage NY Eureka Math 7th Grade Module 4 End of Module Assessment Answer Key

Eureka Math Grade 7 Module 4 End of Module Assessment Task Answer Key

DAY ONE: CALCULATOR ACTIVE
You may use a calculator for this part of the assessment. Show your work to receive full credit.

Question 1.
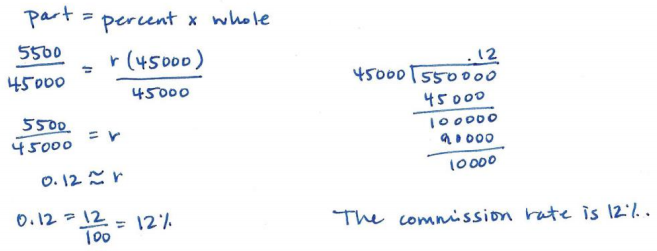
Kara works at a fine jewelry store and earns commission on her total sales for the week. Her weekly paycheck was in the amount of $6,500, including her salary of $1,000. Her sales for the week totaled $45,000. Express her rate of commission as a percent, rounded to the nearest whole number.
Answer:
6500 – 1000 = 5500 in commission
r : commission rate

Question 2.
Kacey and her three friends went out for lunch, and they wanted to leave a 15% tip. The receipt shown below lists the lunch total before tax and tip. The tip is on the cost of the food plus tax. The sales tax rate in Pleasantville is 8.75%.
a. Use mental math to estimate the approximate total cost of the bill including tax and tip to the nearest dollar. Explain how you arrived at your answer.

Answer:
I think the bill will be about $50.00. I found my answer by rounding the total to $40.00. Then, I multiplied by 0.09, which is close to 8.75%. I got $3.60 in tax. I added that to $40.00 to get $43.60, which is close to $44.00. I know 10% of $44.00 is $440, and 5% would be $2.20. So, the total, plus a 15% tip is approximately $44.00 + $6.60 = $50.60.

b. Find the actual total of the bill including tax and tip. If Kacey and her three friends split the bill equally, how much will each person pay including tax and tip?
Answer:

Three people will have to pay $12.18, and one person will have to pay $12.19.

Question 3.
Cool Tees is having a Back to School sale where all t-shirts are discounted by 15%. Joshua wants to buy five shirts: one costs $9.99, two cost $11.99 each, and two others cost $21.00 each.
a. What is the total cost of the shirts including the discount?
Answer:

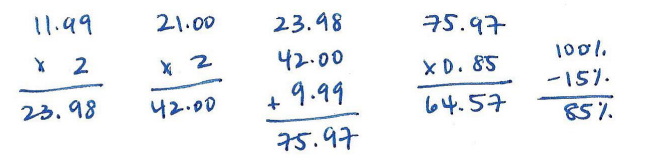
The total cost with the discount is $64.57.

b. By law, sales tax is calculated on the discounted price of the shirts. Would the total cost of the shirts including the 6.5% sales tax be greater if the tax was applied before a 15% discount is taken, rather than after a 15% discount is taken? Explain.
Answer:
The total cost would be the same because of the commutative property of multiplication. Either way, the total cost, including tax and discount, is $68.77
Tax applied after discount
cost = Percent × whole × Rate Tax
= (0.85) (75.97) (1.065)
= 68.77

Tax applied before discount
cost = Percent × whole × Tax Rate
= (1.065) (75.97) (0.85)
= 68.77

c. Joshua remembered he had a coupon in his pocket that would take an additional 30% off the price of the shirts. Calculate the new total cost of the shirts including the sales tax.
Answer:

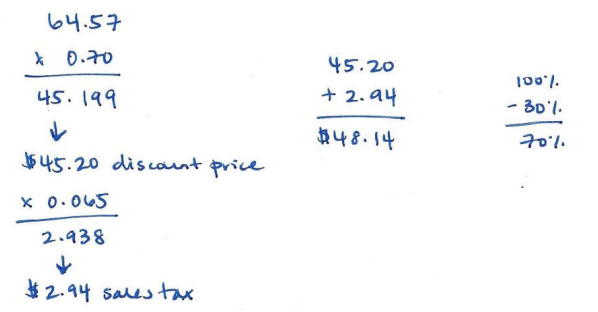
The new total cost of the shirts will be $48.14.

d. If the price of each shirt is 120% of the wholesale price, write an equation and find the wholesale price for a $21 shirt.
Answer:

Question 4.
Tierra, Cameron, and Justice wrote equations to calculate the amount of money in a savings account after one year with \(\frac{1}{2}\)% interest paid annually on a balance of M dollars. Let T represent the total amount of money saved.
Tierra’s Equation: T = 1.05M
Cameron’s Equation: T = M + 0.005M
Justice’s Equation: T = M(1 + 0.005)
a. The three students decided to see if their equations would give the same answer by using a $100 balance. Find the total amount of money in the savings account using each student’s equation. Show your work.
Answer:
T = 1.05($100) = $105
T = $100 + 0.005($100) = $100 + $0.5 = $100.50
T = $100(1 + 0.005) = $100(1.005) = $100.50

b. Explain why their equations will or will not give the same answer.
Answer:
Cameron’s and justice’s equations give the same answers but Tiara’s does not. Tiara’s equation is set up correctly, but she made a mistake when she changed \(\frac{1}{2}\)% to a decimal.
\(\frac{1}{2}\)% = 0.5% = 0.005
Cameron and justice both used the distributive property to solve their equations and the correct decimal of 0.005. This is why their answers are the same.

Question 5.
A printing company is enlarging the image on a postcard to make a greeting card. The enlargement of the postcard’s rectangular image is done using a scale factor of 125%. Be sure to show all other related math work used to answer the following questions.
a. Represent a scale factor of 125% as a fraction and decimal.
Answer:

b. The postcard’s dimensions are 7 inches by 5 inches. What are the dimensions of the greeting card?
Answer:

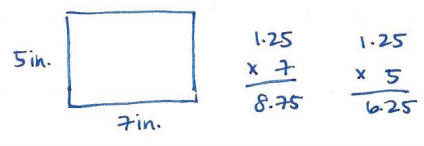
The dimensions of the greeting card are 8.75 in. by 6.25 in.

c. If the printing company makes a poster by enlarging the postcard image, and the poster’s dimensions are 28 inches by 20 inches, represent the scale factor as a percent.
Answer:

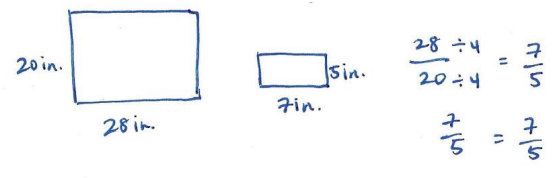
4 is the scale factor, which is 400%.

d. Write an equation, in terms of the scale factor, that shows the relationship between the areas of the postcard and poster. Explain your equation.
Answer:
Area of Poster
A = lw
= (28 in)(20 in)
= 560 in²

Area of Post card
A = lw
= (7 in) (5 in)
= 35 in²
The area of the poster is 16 times the area of the post card. The scale factor is 16, or 1600%. So, my equation is P = 16c, where P is the area of the poster, 16 is the scale factor, and c is the area of the post card.

e. Suppose the printing company wanted to start with the greeting card’s image and reduce it to create the postcard’s image. What scale factor would they use? Represent this scale factor as a percent.
Answer:

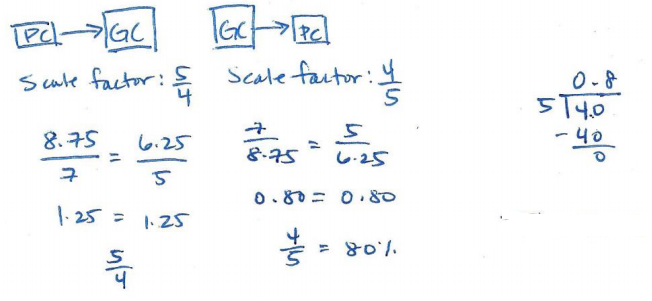
The scale factor is 80%.

f. In math class, students had to create a scale drawing that was smaller than the postcard image. Azra used a scale factor of 60% to create the smaller image. She stated the dimensions of her smaller image as 4\(\frac{1}{6}\) inches by 3 inches. Azra’s math teacher did not give her full credit for her answer. Why? Explain Azra’s error, and write the answer correctly.
Answer:
Azra did not receive full credit because she made an error when changing her decimal to a fraction. She wrote 4\(\frac{2}{10}\) = 4\(\frac{1}{6}\), but it is 4\(\frac{2}{10}\) = 4\(\frac{1}{5}\) because 2 and 10 are divisible by 2.

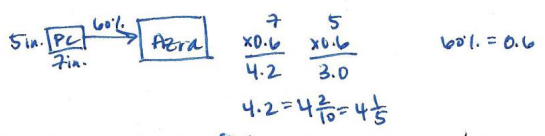
The dimensions of her image are 4\(\frac{1}{5}\) in. by 3 in.

DAY TWO: CALCULATOR INACTIVE
You will now complete the remainder of the assessment without the use of a calculator.

Question 6.
A $100 MP3 player is marked up by 10% and then marked down by 10%. What is the final price? Explain your answer.
Answer:

The final price is $99.00

Question 7.
The water level in a swimming pool increased from 4.5 feet to 6 feet. What is the percent increase in the water level rounded to the nearest tenth of a percent? Show your work.
Answer:

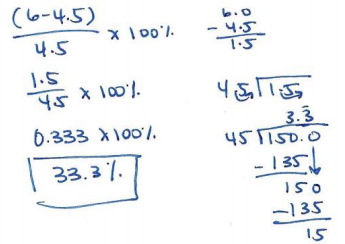
Question 8.
A 5-gallon mixture contains 40% acid. A 3-gallon mixture contains 50% acid. What percent acid is obtained by putting the two mixtures together? Show your work.
Answer:

Question 9.
In Mr. Johnson’s third and fourth period classes, 30% of the students scored a 95% or higher on a quiz. Let n be the total number of students in Mr. Johnson’s classes. Answer the following questions, and show your work to support your answers.
a. If 15 students scored a 95% or higher, write an equation involving n that relates the number of students who scored a 95% or higher to the total number of students in Mr. Johnson’s third and fourth period classes.
Answer:
0.3 n = 15

b. Solve your equation in part (a) to find how many students are in Mr. Johnson’s third and fourth period classes.
Answer:

c. Of the students who scored below 95%, 40% of them are girls. How many boys scored below 95%?
Answer:

21 students are boys.