Engage NY Eureka Math 5th Grade Module 4 Lesson 15 Answer Key
Eureka Math Grade 5 Module 4 Lesson 15 Problem Set Answer Key
Question 1.
Solve. Draw a rectangular fraction model to explain your thinking. Then, write a multiplication sentence. The first one is done for you.
a. \(\frac{2}{3}\) of \(\frac{3}{5}\)
\(\frac{2}{3}\) × \(\frac{3}{5}\) = \(\frac{6}{15}\) = \(\frac{2}{5}\)
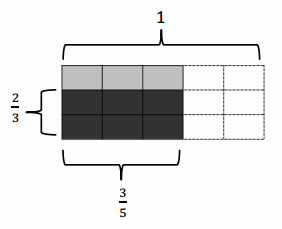
b. \(\frac{3}{4}\) of \(\frac{4}{5}\) =
Answer:
latex]\frac{3}{4}[/latex] of \(\frac{4}{5}\) = \(\frac{3}{5}\).
Explanation:
Given that \(\frac{3}{4}\) of \(\frac{4}{5}\) which is
\(\frac{3}{4}\) × \(\frac{4}{5}\) = \(\frac{3}{5}\)
c. \(\frac{2}{5}\) of \(\frac{2}{3}\)=
Answer:
latex]\frac{2}{5}[/latex] of \(\frac{2}{3}\) = \(\frac{4}{15}\).
Explanation:
Given that \(\frac{2}{5}\) of \(\frac{2}{3}\) which is
\(\frac{2}{5}\) × \(\frac{2}{3}\) = \(\frac{4}{15}\)
d. \(\frac{4}{5}\) × \(\frac{2}{3}\) =
Answer:
latex]\frac{4}{5}[/latex] of \(\frac{2}{3}\) = \(\frac{8}{15}\).
Explanation:
Given that \(\frac{4}{5}\) of \(\frac{2}{3}\) which is
\(\frac{4}{5}\) × \(\frac{2}{3}\) = \(\frac{8}{15}\)
e. \(\frac{3}{4}\) × \(\frac{2}{3}\)=
Answer:
latex]\frac{3}{4}[/latex] of \(\frac{2}{3}\) = \(\frac{1}{2}\).
Explanation:
Given that \(\frac{3}{4}\) of \(\frac{2}{3}\) which is
\(\frac{3}{4}\) × \(\frac{2}{3}\) = \(\frac{1}{2}\)
Question 2.
Multiply. Draw a rectangular fraction model if it helps you, or use the method in the example.
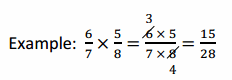
a. \(\frac{3}{4}\) × \(\frac{5}{6}\)
Answer:
latex]\frac{3}{4}[/latex] of \(\frac{5}{6}\) = \(\frac{5}{8}\).
Explanation:
Given that \(\frac{3}{4}\) of \(\frac{5}{6}\) which is
\(\frac{3}{4}\) × \(\frac{5}{6}\) = \(\frac{5}{8}\).
b. \(\frac{4}{5}\) × \(\frac{5}{8}\)
Answer:
latex]\frac{4}{5}[/latex] of \(\frac{5}{8}\) = \(\frac{1}{2}\).
Explanation:
Given that \(\frac{4}{5}\) of \(\frac{5}{8}\) which is
\(\frac{4}{5}\) × \(\frac{5}{8}\) = \(\frac{1}{2}\)
c. \(\frac{2}{3}\) × \(\frac{6}{7}\)
Answer:
latex]\frac{2}{3}[/latex] of \(\frac{6}{7}\) = \(\frac{1}{7}\).
Explanation:
Given that \(\frac{2}{3}\) of \(\frac{6}{7}\) which is
\(\frac{2}{3}\) × \(\frac{6}{7}\) = \(\frac{1}{7}\)
d. \(\frac{4}{9}\) × \(\frac{3}{10}\)
Answer:
latex]\frac{4}{9}[/latex] of \(\frac{3}{10}\) = \(\frac{2}{15}\).
Explanation:
Given that \(\frac{4}{9}\) of \(\frac{3}{10}\) which is
\(\frac{4}{9}\) × \(\frac{3}{10}\) = \(\frac{2}{15}\).
Question 3.
Phillip’s family traveled \(\frac{3}{10}\) of the distance to his grandmother’s house on Saturday. They traveled \(\frac{4}{7}\) of the remaining distance on Sunday. What fraction of the total distance to his grandmother’s house was traveled on Sunday?
Answer:
Philip’s family traveled on Sunday is \(\frac{2}{5}\).
Explanation:
Given that Phillip’s family traveled \(\frac{3}{10}\) of the distance to his grandmother’s house on Saturday, so the remaining is 1 – \(\frac{3}{10}\) which is \(\frac{7}{10}\). So Philip’s family traveled on Sunday is \(\frac{4}{7}\) × \(\frac{7}{10}\) which is \(\frac{2}{5}\).
Question 4.
Santino bought a \(\frac{3}{4}\)-pound bag of chocolate chips. He used \(\frac{2}{3}\) of the bag while baking. How many pounds of chocolate chips did he use while baking?
Answer:
The number of pounds of chocolate chips did he use while baking is \(\frac{1}{2}\) lb.
Explanation:
Given that Santino bought a \(\frac{3}{4}\)-pound bag of chocolate chips and he used \(\frac{2}{3}\) of the bag while baking. So the number of pounds of chocolate chips did he use while baking is \(\frac{3}{4}\) × \(\frac{2}{3}\) which is \(\frac{1}{2}\) lb.
Question 5.
Farmer Dave harvested his corn. He stored \(\frac{5}{9}\) of his corn in one large silo and \(\frac{3}{4}\) of the remaining corn in a small silo. The rest was taken to market to be sold.
a. What fraction of the corn was stored in the small silo?
Answer:
The fraction of the corn was stored in the small silo \(\frac{1}{3}\).
Explanation:
Given that Dave has stored \(\frac{5}{9}\) of his corn in one large silo. Let the total corn be ‘X’, and the amount of corn stored in the silo is \(\frac{5}{9}\)X. The amount of corn remaining is X – \(\frac{5}{9}\)X which is \(\frac{9X – 5X}{9}\) = \(\frac{4X}{9}\). Thus the amount of corn stored in the small silo is \(\frac{3}{4}\) × \(\frac{4}{9}\)X which is \(\frac{1}{3}\)X. Thus the fraction of the corn was stored in the small silo \(\frac{1}{3}\).
b. If he harvested 18 tons of corn, how many tons did he take to market?
Answer:
The amount of corn taken to market is 9 tonnes.
Explanation:
The amount of corn solid in the market is \(\frac{4X}{9}\) – \(\frac{X}{3}\) which is \(\frac{X}{9}\). Thus the amount of corn taken to market is 18 × \(\frac{1}{9}\) which is 9 tonnes.
Eureka Math Grade 5 Module 4 Lesson 15 Exit Ticket Answer Key
Question 1.
Solve. Draw a rectangular fraction model to explain your thinking. Then, write a multiplication sentence.
a. \(\frac{2}{3}\) of \(\frac{3}{5}\) =
Answer:
latex]\frac{2}{3}[/latex] of \(\frac{3}{5}\) = \(\frac{2}{5}\).
Explanation:
Given that \(\frac{2}{3}\) of \(\frac{3}{5}\) which is
\(\frac{2}{3}\) × \(\frac{3}{5}\) = \(\frac{2}{5}\).
b. \(\frac{4}{9}\) × \(\frac{3}{8}\) =
Answer:
latex]\frac{4}{9}[/latex] of \(\frac{3}{8}\) = \(\frac{1}{6}\).
Explanation:
Given that \(\frac{4}{9}\) of \(\frac{3}{8}\) which is
\(\frac{4}{9}\) × \(\frac{3}{8}\) = \(\frac{1}{6}\).
Question 2.
A newspaper’s cover page is \(\frac{3}{8}\) text, and photographs fill the rest. If \(\frac{2}{5}\) of the text is an article about endangered species, what fraction of the cover page is the article about endangered species?
Answer:
The fraction of the cover page is the article about endangered species \(\frac{3}{20}\).
Explanation:
Given that a newspaper’s cover page is \(\frac{3}{8}\) text, and photographs fill the rest, and if \(\frac{2}{5}\) of the text is an article about endangered species. So the fraction of the cover page is the article about endangered species \(\frac{3}{8}\) × \(\frac{2}{5}\) which is \(\frac{3}{20}\).
Eureka Math Grade 5 Module 4 Lesson 15 Homework Answer Key
Question 1.
Solve. Draw a rectangular fraction model to explain your thinking. Then, write a multiplication sentence.
a. \(\frac{2}{3}\) of \(\frac{3}{4}\) =
Answer:
latex]\frac{2}{3}[/latex] of \(\frac{3}{4}\) = \(\frac{1}{2}\).
Explanation:
Given that \(\frac{2}{3}\) of \(\frac{3}{4}\) which is
\(\frac{2}{3}\) × \(\frac{3}{4}\) = \(\frac{1}{2}\).
b. \(\frac{2}{5}\) of \(\frac{3}{4}\) =
Answer:
latex]\frac{2}{5}[/latex] of \(\frac{3}{4}\) = \(\frac{3}{10}\).
Explanation:
Given that \(\frac{2}{5}\) of \(\frac{3}{4}\) which is
\(\frac{2}{5}\) × \(\frac{3}{4}\) = \(\frac{3}{10}\).
c. \(\frac{2}{5}\) of \(\frac{4}{5}\) =
Answer:
latex]\frac{2}{5}[/latex] of \(\frac{4}{5}\) = \(\frac{8}{25}\).
Explanation:
Given that \(\frac{2}{5}\) of \(\frac{4}{5}\) which is
\(\frac{2}{5}\) × \(\frac{4}{5}\) = \(\frac{8}{25}\).
d. \(\frac{4}{5}\) of \(\frac{3}{4}\) =
Answer:
latex]\frac{4}{5}[/latex] of \(\frac{3}{4}\) = \(\frac{3}{5}\).
Explanation:
Given that \(\frac{4}{5}\) of \(\frac{3}{4}\) which is
\(\frac{4}{5}\) × \(\frac{3}{4}\) = \(\frac{3}{5}\).
Question 2.
Multiply. Draw a rectangular fraction model if it helps you.
a. \(\frac{5}{6}\) × \(\frac{3}{10}\)
Answer:
latex]\frac{5}{6}[/latex] of \(\frac{3}{10}\) = \(\frac{1}{4}\).
Explanation:
Given that \(\frac{5}{6}\) of \(\frac{3}{10}\) which is
\(\frac{5}{6}\) × \(\frac{3}{10}\) = \(\frac{1}{4}\).
b. \(\frac{3}{4}\) × \(\frac{4}{5}\)
Answer:
latex]\frac{3}{4}[/latex] of \(\frac{4}{5}\) = \(\frac{3}{5}\).
Explanation:
Given that \(\frac{3}{4}\) of \(\frac{4}{5}\) which is
\(\frac{3}{4}\) × \(\frac{4}{5}\) = \(\frac{3}{5}\).
c. \(\frac{5}{6}\) × \(\frac{5}{8}\)
Answer:
latex]\frac{4}{9}[/latex] of \(\frac{3}{8}\) = \(\frac{1}{6}\).
Explanation:
Given that \(\frac{4}{9}\) of \(\frac{3}{8}\) which is
\(\frac{4}{9}\) × \(\frac{3}{8}\) = \(\frac{1}{6}\).
d. \(\frac{3}{4}\) × \(\frac{5}{12}\)
Answer:
latex]\frac{4}{9}[/latex] of \(\frac{3}{8}\) = \(\frac{1}{6}\).
Explanation:
Given that \(\frac{4}{9}\) of \(\frac{3}{8}\) which is
\(\frac{4}{9}\) × \(\frac{3}{8}\) = \(\frac{1}{6}\).
e. \(\frac{8}{9}\) × \(\frac{2}{3}\)
Answer:
latex]\frac{8}{9}[/latex] of \(\frac{2}{3}\) = \(\frac{16}{27}\).
Explanation:
Given that \(\frac{8}{9}\) of \(\frac{2}{3}\) which is
\(\frac{8}{9}\) × \(\frac{2}{3}\) = \(\frac{16}{27}\).
f. \(\frac{3}{7}\) × \(\frac{2}{9}\)
Answer:
latex]\frac{3}{7}[/latex] of \(\frac{2}{9}\) = \(\frac{2}{21}\).
Explanation:
Given that \(\frac{3}{7}\) of \(\frac{2}{9}\) which is
\(\frac{3}{7}\) × \(\frac{2}{9}\) = \(\frac{2}{21}\).
Question 3.
Every morning, Halle goes to school with a 1-liter bottle of water. She drinks \(\frac{1}{4}\) of the bottle before school starts and \(\frac{2}{3}\) of the rest before lunch.
a. What fraction of the bottle does Halle drink after school starts but before lunch?
Answer:
The fraction of the bottle does Halle drinks after school starts but before lunch is \(\frac{1}{2}\).
Explanation:
Given that Halle goes to school with a 1-liter bottle of water and she drinks \(\frac{1}{4}\) of the bottle before school starts and \(\frac{2}{3}\) of the rest before lunch and the amount left after drinking before school starts are 1 – \(\frac{1}{4}\) which is \(\frac{3}{4}\) and the fraction of the bottle does Halle drinks after school starts but before lunch is \(\frac{2}{3}\) of Amount left
= \(\frac{2}{3}\) × \(\frac{3}{4}\)
= \(\frac{1}{2}\).
b. How many milliliters are left in the bottle at lunch?
Answer:
The amount that left in the bottle at lunch is 250 milliliters.
Explanation:
The amount that left in the bottle at lunch is 1 – (\(\frac{3}{4}\) + \(\frac{1}{2}\))
= \(\frac{1}{4}\), as we know that 1 litre is 1000 milliliters, so \(\frac{1}{4}\) litre is \(\frac{1}{4}\) × 1000 which is 250 milliliters.
Question 4.
Moussa delivered \(\frac{3}{8}\) of the newspapers on his route in the first hour and \(\frac{4}{5}\) of the rest in the second hour. What fraction of the newspapers did Moussa deliver in the second hour?
Question 5.
Rose bought some spinach. She used \(\frac{3}{5}\) of the spinach on a pan of spinach pie for a party and \(\frac{3}{4}\) of the remaining spinach for a pan for her family. She used the rest of the spinach to make a salad.
a. What fraction of the spinach did she use to make the salad?
b. If Rose used 3 pounds of spinach to make the pan of spinach pie for the party, how many pounds of spinach did Rose use to make the salad?