Engage NY Eureka Math 5th Grade Module 3 Lesson 8 Answer Key
Eureka Math Grade 5 Module 3 Lesson 8 Problem Set Answer Key
Question 1.
Add or subtract.
a. 2 + 1\(\frac{1}{5}\) =
b. 2 – 1\(\frac{3}{8}\) =
c. 5\(\frac{2}{5}\) + 2\(\frac{3}{5}\)=
d. 4 – 2\(\frac{2}{7}\) =
e. 9\(\frac{3}{4}\) + 8 =
f. 17 – 15\(\frac{2}{3}\) =
g. 15 + 17 \(\frac{2}{3}\) =
h. 100 – 20\(\frac{7}{8}\) =
Answer:
a.
2 + 1\(\frac{1}{5}\) = 2 + \(\frac{6}{5}\)
lcm of 5 and 1 is 5
\(\frac{10}{5}\) + \(\frac{6}{5}\)
\(\frac{16}{5}\)
3\(\frac{1}{5}\)
b.
2 – 1\(\frac{3}{8}\)
2 – \(\frac{11}{8}\)
lcm is 8
2 – \(\frac{11}{8}\)
\(\frac{16}{8}\) – \(\frac{11}{8}\)
\(\frac{5}{8}\)
c.
5\(\frac{2}{5}\) + 2\(\frac{3}{5}\)
\(\frac{27}{5}\) + \(\frac{13}{5}\)
\(\frac{40}{5}\) = 8
d.
4 – 2\(\frac{2}{7}\) = 4 – \(\frac{16}{7}\)
lcm of 1 and 7 is 7
\(\frac{28}{7}\) – \(\frac{16}{7}\) =\(\frac{12}{7}\)
e.
9\(\frac{3}{4}\) + 8 = \(\frac{39}{4}\) + 8
lcm of 1 and 4 is 4 .
\(\frac{39}{4}\) + \(\frac{32}{4}\) = \(\frac{71}{4}\) =17 \(\frac{2}{4}\)
f.
17 – 15\(\frac{2}{3}\) = 17 – \(\frac{47}{3}\)
lcm is 3
\(\frac{51}{3}\) – \(\frac{47}{3}\) = \(\frac{4}{3}\)
g.
15 + 17 \(\frac{2}{3}\) = 15 + \(\frac{53}{3}\)
lcm is 3
\(\frac{45}{3}\) + \(\frac{53}{3}\) = \(\frac{98}{3}\) = 32\(\frac{1}{3}\)
h.
100 – 20\(\frac{7}{8}\) = 100 – \(\frac{167}{8}\)
lcm is 8
\(\frac{800}{8}\) – \(\frac{167}{8}\) = \(\frac{733}{8}\) = 91\(\frac{5}{8}\)
Question 2.
Calvin had 30 minutes in time-out. For the first 23\(\frac{1}{3}\) minutes, Calvin counted spots on the ceiling. For the rest of the time, he made faces at his stuffed tiger. How long did Calvin spend making faces at his tiger?
Answer:
Number of Minutes of Time-out =30 minutes .
Fraction of Minutes did calvin counted spots on ceiling = 23\(\frac{1}{3}\) minutes
Fraction of Minutes did calvin did faces at his stuffed tiger = x
30 minutes = 23\(\frac{1}{3}\) + x
lcm is 3
30 minutes = \(\frac{70}{3}\) + x
\(\frac{90}{3}\) = \(\frac{70}{3}\) + x
x = \(\frac{90}{3}\) – \(\frac{70}{3}\)
x = \(\frac{20}{3}\)
Therefore, Fraction of Minutes did calvin did faces at his stuffed tiger = x = \(\frac{20}{3}\) .
Question 3.
Linda planned to spend 9 hours practicing piano this week. By Tuesday, she had spent 2\(\frac{1}{2}\) hours practicing. How much longer does she need to practice to reach her goal?
Answer:
Number of Hours required to practice = 9 hours .
Fraction of hours practiced till Tuesday = 2\(\frac{1}{2}\) hours.
Fraction of hours needed to practice to reach goal = x
9 hours = 2\(\frac{1}{2}\) + x
lcm is 2
9 = \(\frac{5}{2}\) + x
\(\frac{18}{2}\) = \(\frac{5}{2}\) + x
x = \(\frac{18}{2}\) – \(\frac{5}{2}\)
x = \(\frac{13}{2}\) .
Therefore Fraction of hours needed to practice to reach goal =x = \(\frac{13}{2}\) .
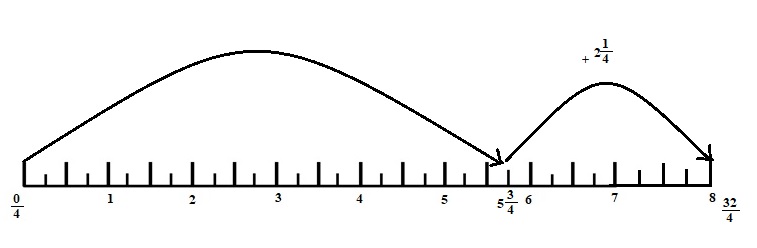
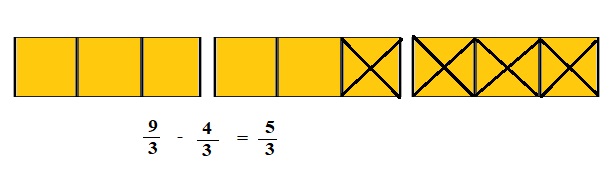
Question 4.
Gary says that 3-1\(\frac{1}{3}\) will be more than 2, since 3 – 1 is 2. Draw a picture to prove that Gary is wrong.
Answer:
Gray is wrong
Explanation :
3-1\(\frac{1}{3}\) = 3 – \(\frac{4}{3}\)
lcm is 3
\(\frac{9}{3}\) – \(\frac{4}{3}\) = \(\frac{5}{3}\)
Eureka Math Grade 5 Module 3 Lesson 8 Exit Ticket Answer Key
Add or subtract.
a. 5 + 1\(\frac{7}{8}\) =
b. 3 – 1\(\frac{3}{4}\) =
c. 7\(\frac{3}{8}\) + 4=
d. 4 – 2\(\frac{3}{7}\) =
Answer:
a.
5 + 1\(\frac{7}{8}\) = 5 + \(\frac{15}{8}\)
lcm of 1 and 8 is 8
\(\frac{40}{8}\) + \(\frac{15}{8}\) = \(\frac{55}{8}\) = 6\(\frac{7}{8}\) .
b.
3 – 1\(\frac{3}{4}\) = 3 – \(\frac{7}{4}\)
lcm is 4
\(\frac{12}{4}\) – \(\frac{7}{4}\) = \(\frac{5}{4}\) =1\(\frac{1}{4}\)
c.
7\(\frac{3}{8}\) + 4= \(\frac{59}{8}\) + 4
lcm of 1 and 8 is 8
\(\frac{59}{8}\) +\(\frac{32}{8}\) = \(\frac{91}{8}\) =11\(\frac{3}{8}\) .
d.
4 – 2\(\frac{3}{7}\) = 4 – \(\frac{17}{7}\)
lcm of 1 and 7 is 7
\(\frac{28}{7}\) – \(\frac{17}{7}\) = \(\frac{11}{7}\) =1\(\frac{4}{7}\) .
Eureka Math Grade 5 Module 3 Lesson 8 Homework Answer Key
Question 1.
Add or subtract.
a. 3 + 1\(\frac{1}{4}\) =
b. 2 – 1\(\frac{5}{8}\) =
c. 5\(\frac{2}{5}\) + 2 \(\frac{3}{5}\) =
d. 4 – 2\(\frac{5}{7}\) =
e. 8\(\frac{4}{5}\) + 7 =
f. 18 – 15\(\frac{3}{4}\) =
g. 16 + 18\(\frac{5}{6}\) =
h. 100 -50\(\frac{3}{8}\) =
Answer:
a.
3 + 1\(\frac{1}{4}\) = 3 + \(\frac{5}{4}\)
lcm of 1 and 4 is 4
\(\frac{12}{4}\) + \(\frac{5}{4}\) = \(\frac{17}{4}\) = 4\(\frac{1}{4}\) .
b.
2 – 1\(\frac{5}{8}\) = 2 – \(\frac{13}{8}\)
lcm is 8
\(\frac{16}{8}\) – \(\frac{13}{8}\) =\(\frac{3}{8}\) .
c.
5\(\frac{2}{5}\) + 2 \(\frac{3}{5}\) = \(\frac{27}{5}\) + \(\frac{13}{5}\) = \(\frac{40}{5}\) = 8.
d.
4 – 2\(\frac{5}{7}\) = 4 – \(\frac{19}{7}\)
lcm of 1 and 7 is 7 .
\(\frac{28}{7}\) – \(\frac{19}{7}\) = \(\frac{9}{7}\) =1\(\frac{2}{7}\)
e.
8\(\frac{4}{5}\) + 7 = \(\frac{44}{5}\) + 7
lcm of 5 and 7 is 35.
\(\frac{308}{35}\) + \(\frac{245}{35}\) = \(\frac{553}{35}\) =15 \(\frac{28}{35}\)
f.
18 – 15\(\frac{3}{4}\) = 18 – \(\frac{63}{4}\)
lcm of 1 and 4 is 4.
18 – \(\frac{63}{4}\) = \(\frac{72}{4}\) – \(\frac{63}{4}\) = \(\frac{9}{4}\) =2\(\frac{1}{4}\)
g.
16 + 18\(\frac{5}{6}\) = 16 + \(\frac{113}{6}\)
lcm is 6
\(\frac{96}{6}\) + \(\frac{113}{6}\) = \(\frac{209}{6}\) = 34\(\frac{5}{6}\)
h.
100 -50\(\frac{3}{8}\) = 100 –\(\frac{403}{8}\)
lcm of 1 and 8 is 8 .
\(\frac{800}{8}\) – \(\frac{403}{8}\) = \(\frac{397}{8}\) = 49\(\frac{5}{8}\) .
Question 2.
The total length of two ribbons is 13 meters. If one ribbon is 7\(\frac{5}{8}\) meters long, what is the length of the other ribbon?
Answer:
The total length of two ribbons = 13 meters.
Fraction of length of one ribbon = 7\(\frac{5}{8}\)
Fraction of length of other ribbon = x
13 = 7\(\frac{5}{8}\) + x
13 = \(\frac{61}{8}\) + x
lcm of 1 and 8 is 8
\(\frac{104}{8}\) = \(\frac{61}{8}\) + x
x = \(\frac{104}{8}\) – \(\frac{61}{8}\)
x = \(\frac{43}{8}\) = 5 \(\frac{3}{8}\)
Therefore, Fraction of length of other ribbon = x = \(\frac{43}{8}\) = 5 \(\frac{3}{8}\) .
Question 3.
It took Sandy two hours to jog 13 miles. She ran 7\(\frac{1}{2}\) miles in the first hour. How far did she run during the second hour?
Answer:
Distance traveled by sandy in 2 hours = 13 miles.
Distance traveled in one hour = 7\(\frac{1}{2}\) miles
Distance traveled in second hour = x
13 miles = 7\(\frac{1}{2}\) + x miles.
13 = \(\frac{15}{2}\) + x
lcm of 1 and 2 is 2 .
\(\frac{26}{2}\) = \(\frac{15}{2}\) + x
x = \(\frac{26}{2}\) – \(\frac{15}{2}\)
x = \(\frac{11}{2}\) = 5\(\frac{1}{2}\) .
Therefore, Distance traveled in second hour = x = \(\frac{11}{2}\) = 5\(\frac{1}{2}\)
Question 4.
Andre says that 5\(\frac{3}{4}\) + 2\(\frac{1}{4}\) = 7\(\frac{1}{2}\) because 7\(\frac{4}{8}\) = 7 \(\frac{1}{2}\). Identify his mistake. Draw a picture to prove that he is wrong.
Answer:
5\(\frac{3}{4}\) + 2\(\frac{1}{4}\) = 7\(\frac{1}{2}\)
5\(\frac{3}{4}\) + 2\(\frac{1}{4}\) = \(\frac{23}{4}\) + \(\frac{9}{4}\) = \(\frac{32}{4}\) = 8
that means andre subtracted \(\frac{3}{4}\) and \(\frac{1}{4}\) instead of adding