Engage NY Eureka Math 4th Grade Module 5 End of Module Assessment Answer Key
Eureka Math Grade 4 Module 5 End of Module Assessment Task Answer Key
Question 1.
a. Partition the tape diagram to show 5 × \(\frac{2}{3}\). Partition the number line to show 10 × \(\frac{1}{3}\) .
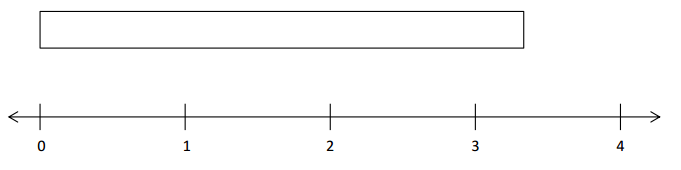
Answer:
5 × \(\frac{2}{3}\) = 3.3.
Explanation:
In the above-given question,
given that,
partition the tape diagram.
5 x 2/3.
5 x 3 = 15.
15 + 2/3 = 17/3.
17/3 = 5.6
10 x 1/3 = 10/3.
10/3 = 3.3.
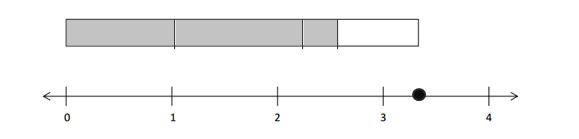
b. Use the models above to explain why 5 × \(\frac{2}{3}\) = 10 × \(\frac{1}{3}\).
Answer:
5 x 2/3 = 10 x 1/3.
Explanation:
In the above-given question,
given that,
5 x 2/3 = 10/3.
5 x 2 = 10.
10 x 1/3 = 10/3.
10 x 1 = 10.
10/3 = 10/3.
5 x 2/3 = 10 x 1/3.
Question 2.
Fill in the circles below with <, =, or > to make true number sentences. Use decomposition or multiplication to justify your answer.
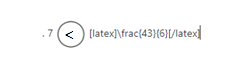
a. 7 ![]() \(\frac{43}{6}\)
\(\frac{43}{6}\)
Answer:
7 < 43/6.
Explanation:
In the above-given question,
given that,
use decomposition or multiplication.
43/6 = 7.1.
7 < 7.1.
7 < 43/6.
b. 11\(\frac{1}{3}\) ![]() \(\frac{34}{3}\)
\(\frac{34}{3}\)
Answer:
11(1/3) = 34/3.
Explanation:
In the above-given question,
given that,
11(1/3) = 11 x 3.
11 x 3 = 33.
33 + 1/3 = 34/3.
34/3 = 11.3.
34/3 = 34/3.
![]()
c. \(\frac{13}{6}\) ![]() \(\frac{38}{12}\)
\(\frac{38}{12}\)
Answer:
(13/6) < 38/12.
Explanation:
In the above-given question,
given that,
13/6 = 2.1.
38/12 = 3.1.
2.1 < 3.1.
13/6 < 38/12.
![]()
Question 3.
Generate a pattern of at least 13 fractions by adding \(\frac{4}{3}\) to \(\frac{1}{3}\) and then continuing to add \(\frac{4}{3}\) to each fraction. Circle each fraction equal to a whole number. Write what you notice about the pattern of whole numbers. The first two fractions are written for you.
\(\frac{1}{3}\), \(\frac{5}{3}\),
Answer:
1/3, 5/3, 9/3, 13/3, 17/3, 21/3, 25/3, 29/3, 33/3, 37/3, 41/3, 45/3, 49/3.
Explanation:
In the above-given question,
given that,
Generate a pattern of at least 13 fractions by adding 4/3 to1/3.
1/3 + 4/3 = 5/3 = 1.6.
5/3 + 4/3 = 9/3 = 3.
9/3 + 4/3 = 13/3 = 4.3.
13/3 + 4/3 = 17/3 = 5.6.
17/3 + 4/3 = 21/3 = 7.
21/3 + 4/3 = 25/3 = 8.3.
25/3 + 4/3 = 29/3 = 9.6.
29/3 + 4/3 = 33/3 = 11.
33/3 + 4/3 = 37/3 = 12.3.
37/3 + 4/3 = 41/3 = 13.6.
41/3 + 4/3 = 45/3 = 15.
45/3 + 4/3 = 49/3 = 16.3.
Question 4.
Find each sum or difference.
a. 6\(\frac{4}{10}\) + 7\(\frac{7}{10}\)
Answer:
6(4/10)+7(7/10) = 14.1.
Explanation:
In the above-given question,
given that,
Find the sum.
6(4/10).
6 x 10 = 60.
60 + 4/10.
64/10 = 6.4.
7(7/10).
7 x 10 = 70.
70 + 7/10.
77/10 = 7.7.
6.4+7.7 = 14.1.
b. 3\(\frac{3}{8}\) + 6\(\frac{5}{8}\) + 1\(\frac{7}{8}\)
Answer:
3(3/8)+6(5/8)+1(7/8)= 11.7.
Explanation:
In the above-given question,
given that,
Find the sum.
3(3/8).
3 x 8 = 24.
24 + 3/8.
27/8 = 3.3.
6(5/8).
6 x 8 = 48.
48 + 5/8.
53/8 = 6.6.
1(7/8).
1 x 8 = 8.
8 + 7/8.
15/8 = 1.8.
6.6+3.3+1.8 = 11.7.
c. 1\(\frac{9}{12}\) – 1\(\frac{4}{12}\)
Answer:
1(9/12)-1(4/12) = 14.1.
Explanation:
In the above-given question,
given that,
Find the sum.
1(9/12).
1 x 12 = 12.
12 + 9/12.
21/12 = 6.4.
1(4/12).
1 x 12 = 12.
12 + 4/12.
16/12 = 7.7.
6.4+7.7 = 14.1.
d. 5\(\frac{2}{5}\) – 1\(\frac{3}{5}\)
Answer:
5(2/5)-1(3/5) = 3.8.
Explanation:
In the above-given question,
given that,
Find the sum.
5(2/5).
5 x 5 = 25.
25 + 2/5.
27/5 = 5.4.
1(3/5).
1 x 5 = 5.
5 + 3/5.
8/5 = 1.6.
5.4 – 1.6 = 3.8.
Question 5.
a. Rewrite 3 × \(\frac{6}{8}\) as the product of a unit fraction and a whole number. Solve.
Answer:
3 x 6/8 = 3.75.
Explanation:
In the above-given question,
given that,
3 x 6/8.
8 x 3 = 24.
24 + 6/8.
30/8 = 3.75.
b. Rewrite 4 × 6\(\frac{2}{3}\) as the product of a unit fraction and a whole number. Solve.
Answer:
4 x 6 x 2/3 = 24.6.
Explanation:
In the above-given question,
given that,
4 x 6 x 2/3.
6 x 4 = 24.
24 x 3 = 72.
72 + 2/3.
74/3 = 24.6.
Question 6.
Determine if the following are true or false. Explain how you know using models or words. Make false problems true by rewriting the right side of the number sentence.
a. 7\(\frac{1}{3}\) = 7 + \(\frac{1}{3}\)
Answer:
No, the sentence is false.
Explanation:
In the above-given question,
given that,
7 x 1/3 = 7/3.
7 + 1/3 = 8/3.
7/3 = 2.3.
8/3 = 2.6.
b. \(\frac{5}{3}\) – \(\frac{3}{3}\) + \(\frac{2}{3}\)
Answer:
5/3 – 3/3 + 2/3 = 4/3.
Explanation:
In the above-given question,
given that,
5/3 – 3/3 + 2/3.
5/3 – 3/3 = 2/3.
5 – 3 = 2.
2/3 + 2/3 = 4/3.
c. \(\frac{13}{6}\) – \(\frac{5}{6}\) = \(\frac{13-5}{6}\)
Answer:
13/6 – 5/6 = 8/6.
Explanation:
In the above-given question,
given that,
13/6 – 5/6.
13 – 5 = 8.
13/6 – 5/6 = 8/6.
d. \(\frac{11}{3}\) = 11 + \(\frac{1}{3}\)
Answer:
11/3 = 11 + 1/3.
Explanation:
In the above-given question,
given that,
11/3 = 3.6.
11 + 1/3.
11 x 3 = 33.
33 + 1/3 = 34/3.
34/3 = 11.3.
e. \(\frac{7}{8}\) + \(\frac{7}{8}\) + \(\frac{7}{8}\) + \(\frac{7}{8}\) = 4 × \(\frac{7}{8}\)
Answer:
True.
Explanation:
In the above-given question,
given that,
7/8 + 7/8 + 7/8 + 7/8.
7/8 = 0.875.
0.8 + 0.8 + 0.8 + 0.8.
4 x 7/8 = 3.2.
f. 5 × 3\(\frac{3}{4}\) = 15 + \(\frac{3}{4}\)
Answer:
True.
Explanation:
In the above-given question,
given that,
5 x 3(3/4).
5 x 3 = 15.
15(3/4) = 15 x 4.
60 + 3/4.
63/4.
5 x 3(3/4) = 15 + 3/4.
Question 7.
The chart to the right shows data Amashi collected about butterfly wingspans.
|
Butterfly |
Wingspan (inches) |
| Monarch | 3\(\frac{7}{8}\) |
| Milbert’s Tortoiseshell | 5\(\frac{5}{8}\) |
| Zebra Swallowtail | 2\(\frac{1}{2}\) |
| Viceroy | 2\(\frac{6}{8}\) |
| Postman | 3\(\frac{3}{8}\) |
| Purple Spotted Swallowtail | 2\(\frac{2}{8}\) |
| Julia | 3\(\frac{2}{4}\) |
| Southern Dogface | 2\(\frac{3}{8}\) |
| Tiger Swallowtail | 3\(\frac{1}{2}\) |
| Regal Fritillary | 3\(\frac{4}{8}\) |
Answer:
Monarch:3(7/8) = 3.8.
Explanation:
In the above-given question,
given that,
the wingspan of the butterflies.
3(7/8) = 3 x 8.
24 + 7/8.
31/8 = 3.8.
Answer:
Milbert’s:5(5/8) = 3.8.
Explanation:
In the above-given question,
given that,
the wingspan of the butterflies.
5(5/8) = 5 x 8.
40 + 5/8.
45/8 = 5.6.
Answer:
Zebra swallow tail:2(1/2) = 3.8.
Explanation:
In the above-given question,
given that,
the wingspan of the butterflies.
2(1/2) = 2 x 2.
4 + 1/2.
5/2 = 2.5.
Answer:
Viceroy:2(6/8) = 2.75.
Explanation:
In the above-given question,
given that,
the wingspan of the butterflies.
2(6/8) = 2 x 8.
16 + 6/8.
22/8 = 2.75.
Answer:
Postman:3(3/8) = 3.3.
Explanation:
In the above-given question,
given that,
the wingspan of the butterflies.
3(3/8) = 3 x 8.
24 + 3/8.
27/8 = 3.3.
Answer:
Purple:2(2/8) = 2.2.
Explanation:
In the above-given question,
given that,
the wingspan of the butterflies.
2(2/8) = 2 x 8.
16 + 2/8.
18/8 = 2.25.
Answer:
Julia:3(2/4) = 3.5.
Explanation:
In the above-given question,
given that,
the wingspan of the butterflies.
3(2/4) = 3 x 4.
12 + 2/4.
14/4 = 3.5.
Answer:
Southern Dog:2(3/8) = 2.3.
Explanation:
In the above-given question,
given that,
the wingspan of the butterflies.
2(3/8) = 2 x 8.
16 + 3/8.
19/8 = 2.3.
Answer:
Tiger:3(1/2) = 3.8.
Explanation:
In the above-given question,
given that,
the wingspan of the butterflies.
3(1/2) = 3 x 2.
6 + 1/2.
7/2 = 3.5.
Answer:
Regal:3(4/8) = 3.8.
Explanation:
In the above-given question,
given that,
the wingspan of the butterflies.
3(4/8) = 3 x 8.
24 + 4/8.
28/8 = 3.5.
a. At the bottom of this page, create a line plot to display the data in the table.
b. What is the difference in wingspan between the widest and narrowest butterflies on the chart?
c. Three butterflies have the same wingspan. Explain how you know the measurements are equal.
Answer:
The three butterflies have the same wingspan = 3.5 in.
Explanation:
In the above-given question,
given that,
the butterflies have the same wingspan.
Tiger swallowtail = 3.5.
Regal Fritillary = 3.5
Julia = 3.5.
Solve each problem. Draw a model, write an equation, and write a statement for each.
d. Amashi wants to display a Postman and Viceroy side by side in a photo box with a width of 6 inches. Will these two butterflies fit? Explain how you know.
Answer:
Yes, the two butterflies will fit.
Explanation:
In the above-given question,
given that,
Amashi wants to display a postman and viceroy side by side in a photo box with a width of 6 inches.
Viceroy = 2.75 in.
Postman = 3.3 in.
2.75 + 3.3 = 6.0.
so, the two butterflies will fit.
e. Compare the wingspan of the Milbert’s Tortoiseshell and the Zebra Swallowtail using >, <, or =.
Answer:
Milbert’s Tortoiseshell > Zebra Swallowtail.
Explanation:
In the above-given question,
given that,
the wingspan of two butterflies.
Milbert’s Tortoiseshell = 5.6 in.
Zebra Swallowtail = 2.5 in.
5.6 > 2.5.
so Milbert’s > Zebra.
f. The Queen Alexandra Birdwing can have a wingspan that is 5 times as wide as the Southern Dogface’s. How many inches can the Birdwing’s wingspan be?
Answer:
Alexandra Birdwing = 11.5 in.
Explanation:
In the above-given question,
given that,
The Queen Alexandra Birdwing can have a wingspan that is 5 times as wide as the Southern Dogface’s.
Southern Dogface’s = 2.3 in.
2.3 x 5 = 11.5.
Alexandra Birdwing = 11.5 in.
g. Amashi discovered a pattern. She started with 2\(\frac{2}{8}\) inches and added \(\frac{1}{8}\) inch to each measurement. List the next four measurements in her pattern. Name the five butterflies whose wingspans match the measurements in her pattern.
Answer:
Zebra Swallow tail, Viceroy, Southern Dogface, Tiger Swallowtail.
Explanation:
In the above-given question,
given that,
Amashi discovered a pattern.
she started with 2(2/8)in.
2 x 2/8 = 8 x 2.
8 x 2 = 16.
16 + 2/8.
18/8 = 2.25.
18/8 + 1/8 = 19/8.
19/8 + 1/8 = 20/8.
20/8 + 1/8 = 21/8.
21/8 + 1/8 = 22/8.
22/8 + 1/8 = 23/8.
19/8 = 2.3.
20/8 = 2.5.
21/8 = 2.6.
22/8 = 2.7.
23/8 = 2.8.