Go through the enVision Math Common Core Grade 4 Answer Key Topic 15 Geometric Measurement: Understand Concepts of Angles and Angle Measurement and finish your homework or assignments.
enVision Math Common Core 4th Grade Answers Key Topic 15 Geometric Measurement: Understand Concepts of Angles and Angle Measurement
Essential Questions:
What are some common geometric terms? How can you measure angles?

enVision STEM Project: Lines and Angles
Do Research Use the Internet or other sources to research the area of the world’s largest bumper car floor. Find where it is located and when it was built.
Journal: Write a Report Include what you found. Also in your report:
- Draw a diagram of a bumper car collision. Use an angle to show how a car might change direction after it collides with something. Measure and label the angle you drew.
- Describe your angle using some of the vocabulary terms in this topic.
Review What You Know
Vocabulary
Choose the best term from the box. Write it on the blank.
- angle
- right angle
- line
- sixth
Question 1.
A(n) _________ is one of 6 equal parts of a whole, written as \(\frac{1}{6}\).
Answer: A sixth is one of 6 equal parts of a whole, written as \(\frac{1}{6}\).
Question 2.
A(n) _________ is a figure formed by two rays that share the same endpoint.
Answer: An angle is a figure formed by two rays that share the same endpoint.
Question 3.
A(n) ___________ is an angle that forms a square corner.
Answer: A right angle is an angle that forms a square corner.
Adding and Subtracting
Find the sum or difference.
Question 4.
45 + 90
Answer:
Given the two numbers 45 and 90
We have to find the sum of 45, 90.
The sum of 45 + 90 = 135.
Question 5.
120 – 45
Answer:
Given the two numbers 120 and 45
We have to find the difference of 120, 45.
The difference of 120 – 45 = 75.
Question 6.
30 + 150
Answer:
Given the two numbers 30 and 150
We have to find the sum of 30, 150.
The sum of 30 + 150 = 180.
Question 7.
180 – 135
Answer:
Given the two numbers 180 and 135
We have to find the difference of 180, 135.
The difference of 180 – 135 = 45.
Question 8.
60 + 120
Answer:
Given the two numbers 60 and 120
We have to find the sum of 60, 120.
The sum of 60 + 120 = 180.
Question 9.
90 – 45
Answer:
Given the two numbers 90 and 45
We have to find the difference of 90, 45.
The difference of 90 – 45 = 45.
Parts of a Whole
Tell the fraction that represents the shaded part of the whole.
Question 10.
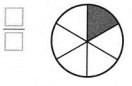
Answer:
The fraction that represents the shaded part of the whole number is 1/6.
Question 11.
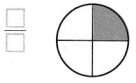
Answer:
The fraction that represents the shaded part of the whole number is 1/4.
Question 12.
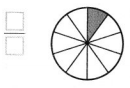
Answer:
The fraction that represents the shaded part of the whole number is 1/10.
Dividing
Find the quotient.
Question 13.
360 ÷ 6
Answer:
The quotient of 360 ÷ 6 = 60
60 is the quotient.
Question 14.
180 ÷ 9
Answer:
The quotient of 180 ÷ 9 = 20
20 is the quotient.
Question 15.
360 ÷ 4
Answer:
The quotient of 360 ÷ 4 = 90
90 is the quotient.
Problem Solving
Question 16.
Make Sense and Persevere Gary has $4. Mary has twice as many dollars as Gary. Larry has 4 fewer dollars than Mary. How much money do Gary, Mary, and Larry have in all?
Answer:
Given that,
Total number of dollars at Gary = $4
Mary has twise as many dollars sa Gray = 2 × $4 = $8.
Larry has 4 fewer dollars than Mary = $8 – 4 = $4.
Total money with Gary, Marry, and Larry = $8 + $4 + $4 = $16.
Pick a Project
PROJECT 15A
Can you find angles in stringed instruments?
Project: Make a Stringed Instrument

PROJECT 15B
How are angles important in origami?
Project: Present an Origami Animal

PROJECT 15C
How are angles formed by airplane paths?
Project: Trace a Flight Plan

3-ACT MATH PREVIEW
Math Modeling
Game of Angles

I can … model with math to solve a problem that involves measuring angles and computing with angle measures.
Lesson 15.1 Lines, Rays, and Angles
Solve & Share
A right angle forms a square corner, like the one shown below. Find examples of right angles in your classroom. Draw two angles that are open less than the right angle. Solve this problem any way you choose.
I can … recognize and draw lines, rays, and different types of angles.

Look Back! Reasoning Draw an angle that is open more than a right angle.
Essential Question
What Are Some Common Geometric Terms?
Visual Learning Bridge
Point, line, line segment, ray, right angle, acute angle, obtuse angle, and straight angle are common geometric terms.
An angle is formed by two rays that have the same endpoint.
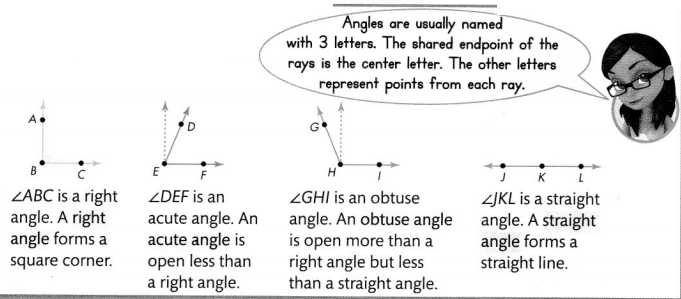
Convince Me! Look for Relationships Complete each figure to show the given angle.

Guided Practice
Do You Understand?
Question 1.
What geometric term describes a part of a line that has one endpoint? Draw an example.
Answer:
A ray is a part of a line that has one endpoint and continues on forever in one direction.
![]()
Question 2.
What geometric term describes a part of a line that has two endpoints? Draw an example.
Answer:
A line segment is a part of a line with two endpoints.
![]()
Question 3.
What geometric term describes an angle that forms a square corner? Draw an example.
Answer:
A right angle forms a square corner.
Do You Know How?
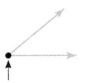
For 4-7, use geometric terms to describe what is shown.
Question 4.
![]()
Answer:
∠PX represents the line segment with two end points.
Question 5.

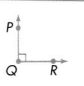
Answer:
∠PQR is a right angle triangle. A right angle forms a forms a square corner.
Question 6.
![]()
Answer:
∠BY is a straight angle.
Question 7.
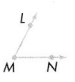
Answer:
∠LMN is an acute angle. An acute angle is open less than a right angle.
Independent Practice
For 8-11, use geometric terms to describe what is shown.
Question 8.
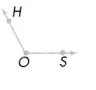
Answer:
∠HOS is an obtuse angle. An obtuse angle is open more than a right angle but less than a straight angle.
Question 9.
![]()
Answer:
∠BD represents the line segment with two endpoints.
Question 10.
![]()
Answer: ∠BY is a straight angle.
Question 11.
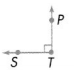
Answer:
∠STP is a right angle.
For 12-15, draw the geometric figure for each term.
Question 12.
Line segment
Answer:
![]()
Question 13.
Point
Answer:
•
Question 14.
Ray
Answer:
![]()
Question 15.
Line
Answer:

Problem Solving
For 16-18, use the map of Nevada. Write the geometric term that best fits each description. Draw an example.
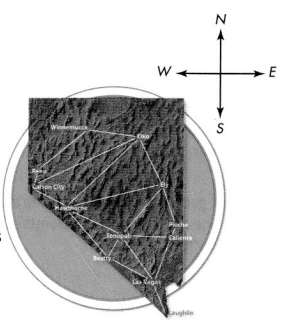
Question 16.
Be Precise The route between 2 cities.
Answer:
Question 17.
The cities
Answer:
Question 18.
The corner formed by the north and west borders
Answer:
Question 19.
Vocabulary Write a definition for right angle. Draw a right angle. Give 3 examples of right angles in the classroom.
Answer:
Question 20.
Higher Order Thinking Nina says she can make a right angle with an acute angle and an obtuse angle that have a common ray. Is Nina correct? Draw a picture and explain.
Answer: If an angle is acute, it can’t also be a right angle.
Assessment Practice
Question 21.
Which geometric term describes ∠HJK?
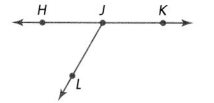
A. Acute angle
B. Obtuse angle
C. Right angle
D. Straight angle
Answer:
The geometric term ∠HJK represents a straight angle.
Thus the answer is option D.
Question 22.
Lisa drew 2 rays that share an endpoint. Which of the following is Lisa’s drawing?
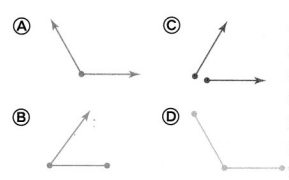
Answer: D
Lesson 15.2 Understand Angles and Unit Angles
Solve & Share
If a clock shows it is 3 o’clock, how could you describe the smaller angle made by the two hands of the clock? Solve this problem any way you choose.
I can … use what I know about fractions to measure angles.

Look Back! At 3 o’clock, what two fractions do the hands divide the clock into?
Essential Question
What is the Unit Used to Measure Angles?
Visual Learning Bridge
An angle is measured with units called degrees. An angle that turns through \(\frac{1}{360}\) of a circle is called a unit angle. How can you determine the angle measure of a right angle and the angles that turn through \(\frac{1}{6}\) and \(\frac{2}{6}\) of a circle?
You measure length in inches, area in square centimeters, and capacity in ounces. You measure an angle in degrees, o. A full circle has an
angle measure of 360°.
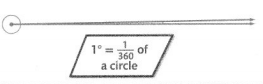
Divide to find the angle measure of a right angle.
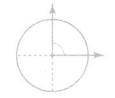
Right angles divide a circle into 4 equal parts.
360° ÷ 4 = 90°
The angle measure of a right angle is 90°.
Divide to find the measure of an angle that turns through \(\frac{1}{6}\) of a circle.
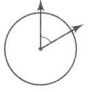
\(\frac{1}{6}\) of a circle is one part of the circle that is divided into 6 equal parts.
360° ÷ 6 = 60°
The angle measure is 60°.
Add to find the measure of an angle that turns through \(\frac{2}{6}\) of a circle.
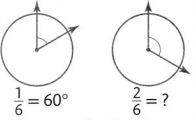
Remember \(\frac{2}{6}\) = \(\frac{1}{6}\) + \(\frac{1}{6}\)
Add to calculate the measure of \(\frac{2}{6}\) of a circle.
60° + 60° = 120° The angle measure of of a circle is 120°.
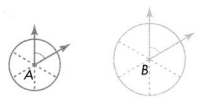
Convince Me! Critique Reasoning Susan thinks the measure of angle B is greater than the measure of angle A. Do you agree? Explain.
Another Example!
Find the fraction of a circle that an angle with a measure of 45° turns through
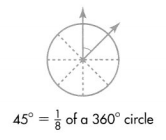
A 45° angle turns through \(\frac{45}{360}\) of a circle.
45° × 8 = 360°, so 45° is \(\frac{1}{8}\) of 360°.
One 45° angle is \(\frac{1}{8}\) of a circle.
Guided Practice
Do You Understand?
Question 1.
What fraction of the circle does a 120° angle turn through?
Answer:
A circle contains 360°
To find the fraction of the circle’s 120° angle.
Divide 120° by 360°
120°/360° = 1/3
Thus the fraction of the circle that does a 120° angle turn through is 1/3.
Question 2.
Mike cuts a pie into 4 equal pieces. What is the angle measure of each piece? Write and solve an equation.
Answer:
Given,
Mike cuts a pie into 4 equal pieces.
A circle contains 360°
360/90 = 4
90 degrees because when you cut each of them they will each measure 90 degrees.
Do You Know How?
Question 3.
A circle is divided into 9 equal parts. What is the angle measure of one of those parts?
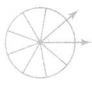
Answer:
Given that,
A circle is divided into 9 equal parts.
There are 360 degrees in a circle.
That means that we first divide 360 by 9.
We have the measure for one of the nine parts of the circle, but we need two.
All we do is multiply 40 by 2 to get 80 degrees.
Question 4.
An angle turns through of the circle. What is the measure of this angle?
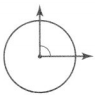
Answer:
An angle turns through the circle.
There are 360 degrees in a circle.
That means that we first divide 360 by 4.
360 ÷ 4 = 90
Thus the measure of the angle of the above circle is 90 degrees.
Independent Practice
For 5-8, find the measure of each angle.
Question 5.
The angle turns through \(\frac{1}{5}\) of the circle.
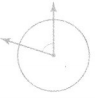
Answer:
An angle turns through the circle.
There are 360 degrees in a circle.
That means that we first divide 360 by 5.
360 ÷ 5 = 72
Thus the measure of the angle of the above circle is 72 degrees.
Question 6.
The angle turns through \(\frac{3}{8}\) of the circle.
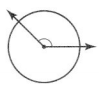
Answer:
An angle turns through the circle.
There are 360 degrees in a circle.
That means that we first divide 360 by \(\frac{3}{8}\).
360 × \(\frac{3}{8}\) = 135
Thus the measure of the angle of the above circle is 135 degrees.
Question 7.
The angle turns through \(\frac{2}{5}\) of the circle.
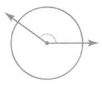
Answer:
The angle turns through \(\frac{2}{5}\) of the circle.
There are 360 degrees in a circle.
That means that we first divide 360 by \(\frac{2}{5}\).
360 × \(\frac{2}{5}\) = 144
Thus the measure of the angle of the above circle is 144 degrees.
Question 8.
The angle turns through \(\frac{2}{6}\) of the circle.

Answer:
The angle turns through \(\frac{2}{6}\) of the circle.
There are 360 degrees in a circle.
That means that we first divide 360 by \(\frac{2}{6}\).
360 × \(\frac{2}{6}\) = 120
Thus the measure of the angle of the above circle is 120 degrees.
Problem Solving
Question 9.
Use the clock to find the measure of the smaller angle formed by the hands at each time.

a. 3:00
b. 11:00
c. 2:00
Answer:

11:00
Thus the correct answer is option B.
Question 10.
Algebra Jacey wrote an equation to find an angle measure. What do variables a and b represent in Jacey’s equation? 360° ÷ a = b
Answer:
We know that Jacey wrote an equation to find an angle measure.
The equation is as follows:
360 ÷ a = b
So, if the angle is 360 degrees is a central angle, i.e, an angle between 2 radii in a circle, then
a = the number of equal parts the circle is divided.
b = the measure of the central angle of each part.
Question 11.
enVision® STEM A mirror can be used to reflect a beam of light at an angle. What fraction of a circle would the angle shown turn through?
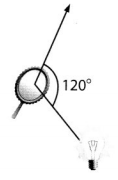
Answer:
Given,
A mirror can be used to reflect a beam of light at an angle.
120° ÷ 360° = 1/3
The fraction of a circle would the angle turn is 1/3.
Question 12.
Malik paid $32.37 for three books. One book cost $16.59. The second book cost $4.27. How much did the third book cost? Use bills and coins to solve.

Answer:
Given,
Malik paid $32.37 for three books. One book cost $16.59. The second book cost $4.27.
$16.59 + $4.27 = $20.86
$32.37 – $20.86 = $11.51
Thus the cost of third book is $11.51
Question 13.
Make Sense and Persevere A pie was cut into equal parts. Four pieces of the pie were eaten. The 5 pieces that remained created an angle that measured 200°. What was the angle measure of one piece of pie?
Answer:
Given that,
A pie was cut into equal parts.
Four pieces of the pie were eaten.
The 5 pieces that remained created an angle that measured 200°.
200/5 = 40
Thus the angle measure of one piece of pie is 40 degrees.
Question 14.
Higher Order Thinking Jake cut a round gelatin dessert into 8 equal pieces. Five of the pieces were eaten. What is the angle measure of the dessert that was left?
Answer:
Given,
Jake cut a round gelatin dessert into 8 equal pieces.
Five of the pieces were eaten.
Fraction is the number of pieces eaten by the total number of pieces.
5/8
360 × 5/8 = 225
Thus the angle measure of the desert that was left.
Assessment Practice
Question 15.
Select all choices that show an angle measure of 120°. Use the clock to help.

☐ 10 o’clock
☐ \(\frac{2}{6}\) of a pie
☐ \(\frac{2}{3}\) of a circle
☐ 4 o’clock
☐ 8 o’clock
Answer: \(\frac{2}{6}\) of a pie
Lesson 15.3 Measure with Unit Angles
Solve & Share
The smaller angles on the tan pattern block shown each measure 30°. How can you use the angles on the pattern block to determine the measure of the angle below? Solve this problem any way you choose.
I can … use angles I know to measure angles I do not know.

Look Back! Two right angles make a straight angle. How many 45° angles form a straight angle? Explain.
Essential Question
How Can You Measure Angles?
Visual Learning Bridge
Holly traced around a trapezoid pattern block. She wants to find the measure of the angle formed shown to the right. What can Holly use to measure the angle?
The measure of a unit angle is 1 degree. Just like adding inches + inches, you can add degrees + degrees. So 5° = 1° + 1° + 1° + 1° + 1°
or 5 × 1°
Use an angle you know to find the measure of another angle.
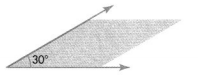
The smaller angle of the tan pattern block measures 30°.
A 30-degree angle turns through 30 one-degree angles.
The angle of the trapezoid pattern block is equal to 2 of the smaller angles of the tan pattern block. Each smaller angle is 30°.
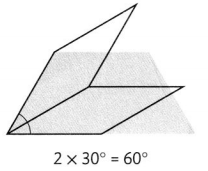
The measure of the trapezoid angle is 60°.
A 60-degree angle turns through 60 one-degree angles.
Convince Me! Generalize What do you notice about the number of one-degree angles in an angle measure?
Guided Practice
Do You Understand?
Question 1.
How many 30° angles are in a 180° angle? Explain.
![]()
Answer:
180 ÷ 30 = 6
Thus there are 6 30° angles are in a 180° angle.
Question 2.
How many 15° angles are in a 180° angle? Use your answer to Exercise 1 to explain.
Answer:
180 ÷ 15 = 12
Thus there are 12 15° angles are in a 180° angle.
Do You Know How?
For 3-4, use angles you know to find the measure of each angle. Explain how the angles in the square can help.
Question 3.

Answer:
By seeing the above figure we can say that it is a right angle.
90 ÷ 2 = 45 degrees
Question 4.
Answer:
By seeing the above figure we can say that it is an obtuse angle.
90° + 45° = 135°
Independent Practice
For 5-13, find the measure of each angle. Use pattern blocks to help.
Question 5.

Answer:
The measure of the angle is 70 degrees.
Question 6.
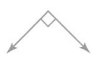
Answer:
The measure of the angle is 90 degrees.
Question 7.
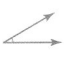
Answer:
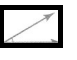
The measure of the angle is 60 degrees.
Question 8.

Answer:
The measure of the angle is 110 degrees.
Question 9.
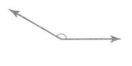
Answer:
The measure of the angle is 120 degrees.
Question 10.

Answer:
The measure of the angle is 90 degrees.
Question 11.
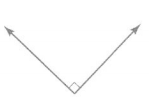
Answer:
The measure of the angle is 90 degrees.
Question 12.

Answer:
The measure of the angle is 180 degrees.
Question 13.
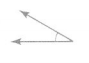
Answer:
The measure of the angle is 90 degrees.
Problem Solving
Question 14.
Use Appropriate Tools What is the measure of the angle of the yellow hexagon pattern block?
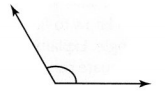
Answer:
Question 15.
What is the measure of the smaller angle formed by the clock hands when it is 5:00?

Answer: 120 degrees
Question 16.
How many 30° angles are in a circle? Write and solve a multiplication equation to explain.
Answer:
The total angle in a circle is 360 degrees
360°/30° = 12
Thus there are 120 30° angles in a circle.
Question 17.
How many unit angles make up the smaller angle formed by the hands of a clock when it is 3:00? Explain.
Answer:
3/12 = x°/360°
1/4 = x°/360°
x° = 90°
Question 18.
Veronica purchases a rug with a length of 16 feet and a width of 4 feet. One fourth of the rug is purple and the rest is blue. What is the area of the blue part of the rug?
Answer:
Veronica purchases a rug with a length of 16 feet and a width of 4 feet.
One-fourth of the rug is purple and the rest is blue.
A = base × height
Area = 16 × 4 = 64 sq. ft
Determine the blue area:
64 sq. ft — 1
x —- 3/4
x = 3/4 × 64
x = 192/4
x = 48 sq.ft
Question 19.
Higher Order Thinking The hands of a clock form a 120° angle. Name two different times it could be.
Answer:
The 120° angles make up 1/3 of one full rotation of the hands-on clock, with a full rotation divided up into 12 equal sections. 1/3 of those 12 sections would be 4 sections, and since we are looking for exact hours that represent this angle, we need four sections forming each of the 120° angles with the minute hand on the clock being at 12. Therefore, the hour hand can be at the 4 for 4 o’clock and it could also be at the 8 for 8 o’clock.
Assessment Practice
Question 20.
The clock reads 9:00. What is the angle measure?

A. 90°
B. 180°
C. 270°
D. 360°
Answer:
A. 90°
The angle measure is 90 degrees.
Thus the correct answer is option A.
Question 21.
How many 60° angles are in 360° angle?

A. 3
B. 6
C. 10
D. 12
Answer: 6
Explanation:
360/60 = 6
There are 6 60° angles are in 360° angle.
Thus the correct answer is option B.
Lesson 15.4 Measure and Draw Angles
Solve & Share
Find the measure of ZABC. Solve this problem any way you choose.
I can … use a protractor to measure and draw angles.

Look Back! Use Appropriate Tools Use the protractor to draw an angle that measures 110°.

Essential Question
How Do You Use a Protractor?
Visual Learning Bridges
A protractor is a tool that is used to measure and draw angles. A partially folded crane is shown at the right. Measure ∠PQR.
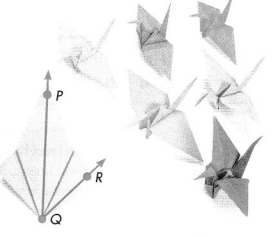
The angle, ∠PQR can also be written as ∠RQP.
Measure Angles
Measure ∠PQR.
Place the protractor’s center on the angle’s vertex, Q. Place one of the 0° marks on \(\overrightarrow{Q R}\). Read the measure where \(\overrightarrow{Q P}\) crosses the protractor. If the angle is acute, use the lesser number. If the angle is obtuse, use the greater number.
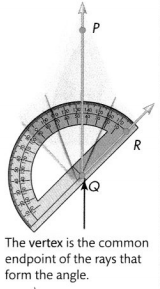
The measure of ∠PQR is 45°.
Draw Angles
Draw an angle that measures 130°.
Draw \(\overrightarrow{T U}\). Place the protractor so the center is over point T, and one of the 0° marks is on \(\overrightarrow{T U}\). Place a point at 130°. Label it W. Draw \(\overrightarrow{T W}\).
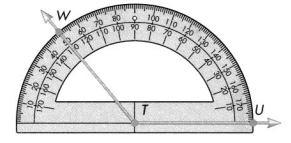
The measure of ∠WTU is 130°.
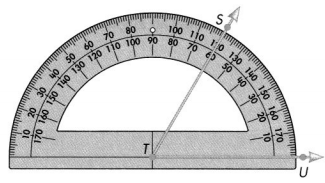
Convince Me! Be Precise How do you know the measure of ∠UTS is 60° and not 120°?
Guided Practice
Do You Understand?
Question 1.
What is the angle measure of a straight line?
![]()
Answer: The angle measure of a straight line is 0° or 180°
Question 2.
What are the vertex and rays of ∠ABC? Explain.
Answer:
The vertex is the common point at which the two lines or rays are joined. Point B in the figure above is the vertex of the angle ∠ABC.
Do You Know How?
For 3-4, use a protractor to measure each angle.
Question 3.
Answer: 50 degrees
Question 4.

Answer: 120 degrees
For 5-6, use a protractor to draw each angle.
Question 5.
110°
Answer:
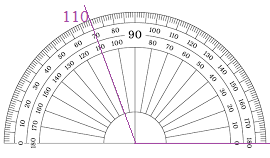
Question 6.
50°
Answer:

Independent Practice
For 7-14, measure each angle. Tell if each angle is acute, right, or obtuse.
Remember an acute angle is less than 90° and an obtuse angle is greater than 90° but less than 180°.
Question 7.

Answer: The above angle is greater than 90° so it is an obtuse angle.
Question 8.
![]()
Answer:
The above angle is less than 90° so it is an acute angle.
Question 9.

Answer:
The above angle is less than 90° so it is an acute angle.
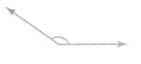
Question 10.
Answer:
The above angle is greater than 90° so it is an obtuse angle.
Question 11.
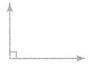
Answer:
The above angle is equal to 90° so it is a right angle.
Question 12.
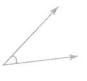
Answer:
The above angle is less than 90° so it is an acute angle.
Question 13.
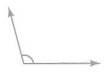
Answer:
The above angle is greater than 90° so it is an obtuse angle.
Question 14.
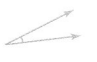
Answer:
The above angle is less than 90° so it is an acute angle.
For 15-18, use a protractor to draw an angle for each measure.
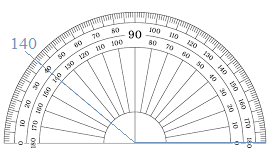
Question 15.
140°
Answer:
Question 16.
180°
Answer:
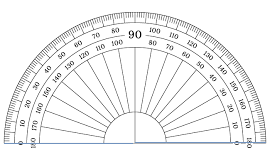
Question 17.
65°
Answer:
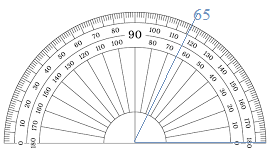
Question 18.
25°
Answer:
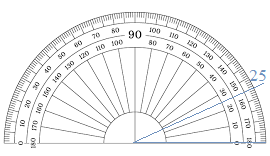
Problem Solving
Question 19.
Measure all the angles created by the intersection of Main Street and Pleasant Street. Explain how you measured.

Answer: 25 degrees
Question 20.
Use a protractor to find the measure of the angle, then use one of the angle’s rays to draw a right angle. Find the measure of the the angle that is NOT a right angle.
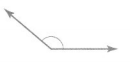
Answer: 110 degrees
Question 21.
Critique Reasoning Gail and 3 friends share half a pie. Each piece of pie is the same size. Gail believes each piece of pie has an angle measure of 25°. Is Gail correct? Explain.
Answer:
Given,
Gail and 3 friends share half a pie. Each piece of pie is the same size.
Gail believes each piece of the pie has an angle measure of 25°.
Half of a pie is 50%, divide that by three and that equals about 16.67 if you round it, but if each piece has an angle of 25, those pieces aren’t equal.
Question 22.
Janet made 5 three-point shots in her first game and 3 in her second game. She also made 4 two-point shots in each game. How many total points did Janet score in the two games?
Answer: Janet score 35 points
Question 23.
Higher Order Thinking Maya designed two intersecting roads. She drew the roads so one of the angles at the intersection was 35o. What are the three other angle measurements formed by the intersection?
Answer:
To find the other three angles in the intersection, we need to know that in an intersection of two lines, one angle is the supplement of the other, and the other two are equal to the first and the second one, that is, if the first angle is x, the values of the four angles are
x, 180 – x, x and 180 – x
so if one angle is 35 degrees, we have that the three other angles are 145 degrees, 35 degrees, and 145 degrees.
Assessment Practice
Question 24.
Find the measure of the angle shown.
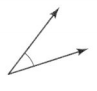
Answer: 35 degrees
Question 25.
Find the measure of the angle shown.
Answer: 110 degrees
Lesson 15.5 Add and Subtract Angle Measures
Solve & Share
Draw \(\overrightarrow{B C}\) that divides ∠ABD into two smaller angles. Measure each angle. Solve this problem any way you choose.
I can … use addition and subtraction to solve problems with unknown angle measures.
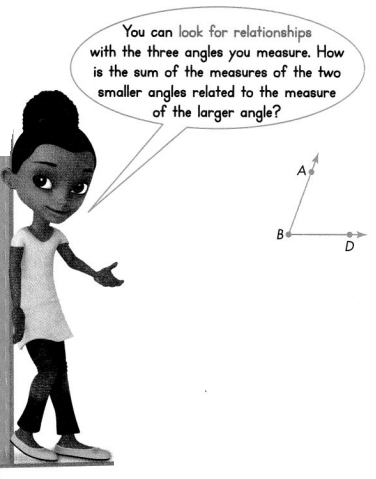
Look Back! How can you relate the measures of the two smaller angles to the measure of the larger angle above using an equation?
Essential Question
How Can You Add and Subtract to Find Unknown Angle Measures?
Visual Learning Bridge
Elinor designs wings for biplanes. First she draws a right angle, ∠ABC. Then she draws \(\overrightarrow{B E}\). She finds ∠EBC measures 30°. How can Elinor find the measure of ∠ABE without using a protractor?
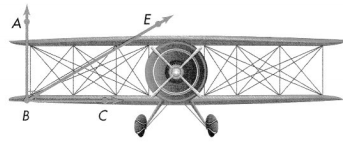
∠ABC is decomposed into two non-overlapping parts.
∠EBC and ∠ABE do not overlap, so the measure of right ∠ABC is equal to the sum of the measures of its parts.
The measure of ∠ABC equals the measure of ∠ABE plus the measure of ∠EBC.
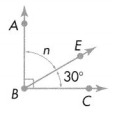
All right angles measure 90°
Write an equation to determine the missing angle measure.
n + 30° = 90°
Solve the equation.
n = 90° – 30°
n = 60°

The measure of ∠ABE is 60°.
Convince Me! Make Sense and Persevere ∠ABD is a straight angle. What is the measure of ∠ABE if the measure of ∠DBC is 115° and the measure of ∠CBE is 20°? How did you decide? Write and solve an equation.
Guided Practice
Do You Understand?
Question 1.
Use the information below to draw and label a diagram. ∠PQR measures 45°. ∠RQS measures 40°. ∠PQR and ∠RQS do not overlap. Write and solve an equation to find the measure of ∠PQS.
Answer:
∠PQR + ∠RQS + n = 90
Do You Know How?
For 2-3, use the diagram to the right of each exercise. Write and solve an equation to find the missing angle measure.
Question 2.
What is the measure of ∠EBC if ∠ABE measures 20°?
Answer:
∠EBC + ∠ABE = 90°
∠EBC + 20° = 90°
∠EBC = 90° – 20°
∠EBC = 70°
Question 3.
What is the measure of ∠AEB if ∠CEB measures 68°?
Answer:
∠AEB + ∠CEB = 180°
∠AEB + 68° = 180°
∠AEB = 180° – 68°
∠AEB = 112°
Independent Practice
For 4-7, use the diagram to the right. Write and solve an addition or subtraction equation to find the missing angle measure.
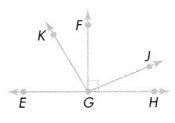
Question 4.
What is the measure of ∠FGJ if ∠JGH measures 22°?
Answer:
∠FGJ + ∠JGH = 90°
∠FGJ + 22° = 90°
∠FGJ = 90° – 22°
∠FGJ = 68°
Question 5.
What is the measure of ∠KGF if ∠EGK measures 59°?
Answer:
∠KGF + ∠EGK = 90°
∠KGF + 59°= 90°
∠KGF = 90° – 59°
∠KGF = 31°
Question 6.
Use the angle measures you know to write an equation to find the angle measure of ∠EGH. What kind of angle is ∠EGH?
Answer:
∠EGK + ∠KGF + ∠FGJ + ∠JGH = 180°
Question 7.
Which two non-overlapping angles that share a ray make an obtuse angle? Use addition to explain.
Answer: ∠KGH and ∠EGJ are the two non-overlapping angles that share a ray that makes an obtuse angle.
Problem Solving
Question 8.
Shane says a straight angle always has 180° degrees. Is Shane correct? Explain.
Answer: Yes Shane is correct.
Question 9.
Model with Math Talla earns 85¢ for cans she recycles. If she gets a nickel for each can, how many cans does Talla recycle? Draw a bar diagram to represent how to solve the problem.
Answer:
Question 10.
Alex draws an angle that measures 110°. He then draws a ray that divides the angle into 2 equal parts. What is the measure of each smaller angle?
Answer:
To solve for this use the expression 110/2 since you are dividing an angle into two equal parts.
When you simplify, you should get 55 degrees as the measure of each angle.
Question 11.
Six angles share a vertex. Each of the angles has the same measure. The sum of the measures of the angles is 330°. What is the measure of one angle?
Answer:
Given,
Six angles share a vertex. Each of the angles has the same measure.
The sum of the measures of the angles is 330°.
The measure of one angle is 55 because 330 divided by six is 55
Question 12.
Higher Order Thinking Li uses pattern blocks to make a design. He puts 5 pattern blocks together, as shown in the diagram. The measure of ∠LJK is 30°. Name all the 60° angles shown that have point J as a vertex.
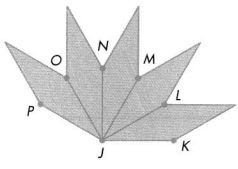
Answer:
Li uses pattern blocks to make a design.
He puts 5 pattern blocks together, as shown in the diagram.
The measure of ∠LJK is 30°.
divide 120 by 4 you get 30 then multiply 30 by 2.
Assessment Practice
Question 13.
Carla drew two acute non-overlapping angles that share a ray and labeled them ∠JLK and ∠KLM. The two angles have different measures. Carla says ∠JLM is greater than a right angle.

Part A
Is it possible for Carla to be correct? Write to explain.
Answer: No, because the acute angle is less than the right angle.
Part B
Write an equation showing one possible sum for Carla’s angles.
Answer: ∠JLK + ∠KLM = 90 degrees
Lesson 15.6 Problem Solving
Use Appropriate Tools
Solve & Share
Caleb is standing next to the tallest building in a city. Determine the measure of the 3 angles with the vertex at the tallest building and rays on the music hall, the live theater, and the art museum. Tell what tool you used and explain why the measures make sense relative to each other.
I can … use appropriate tools strategically to solve problems.
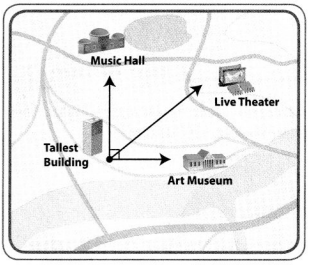
Thinking Habits
Be a good thinker! These questions can help you.
- Which tools can I use?
- Why should I use this tool to help me solve the problem?
- Is there a different tool I could use?
- Am I using the tool appropriately?
Look Back! Use Appropriate Tools Could you use a ruler to find the angle measures? Explain.
Essential Question
How Can You Select and Use Appropriate Tools to Solve Problems?
Visual Learning Bridge
Trevor and Holly are drawing trapezoids to make a design. They need to find the measures of the angles formed by the sides of the trapezoid and the length of each side of the trapezoid. What tools are needed to find the measures of the angles and the lengths of the sides?

What do you need to do to copy the trapezoid?
I need to measure the angles, then measure the sides.
Which tool can I use to help me solve this problem?
I can
- decide which tool is appropriate.
- explain why it is the best tool to use.
- use the tool correctly.
Here’s my thinking.
Use a protractor to measure the angles. The angles measure 120° and 60°.

Then, use a ruler to measure the length of each side. The lengths are \(\frac{3}{4}\) inch, \(\frac{3}{4}\) inch, \(\frac{3}{4}\) inch, and 1\(\frac{1}{2}\) inches.
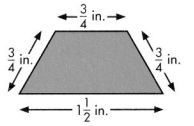
Convince Me! Use Appropriate Tools What other tools could be used to solve this problem? Why are a protractor and a ruler more appropriate than other tools?
Guided Practice
Lee brought 1\(\frac{3}{5}\) pounds of apples to the picnic. Hannah brought \(\frac{4}{5}\) pound of oranges. Lee said they brought 2\(\frac{2}{5}\) pounds of fruit in all. Lee needs to justify that 1\(\frac{3}{5}\) + \(\frac{4}{5}\) = 2\(\frac{2}{5}\)

Question 1.
What tool could Lee use to justify the sum?
Answer: Fraction strips
Question 2.
How can Lee use a tool to justify the sum? Draw pictures of the tool you used to explain.
Answer:
Independent Practice
Use Appropriate Tools
What are the measures of the sides and angles of the parallelogram shown? Use Exercises 3-5 to help solve.

Question 3.
What tools can you use to solve this problem?
Answer:
Question 4.
Explain how to use the tool you chose to find the measures of the angles. Label the figure with the measures you find.
Answer:
Question 5.
Explain how to use the tool you chose to find the lengths of the sides. Label the figure with the measures you find.
Answer:
Problem Solving
Performance Task
Mural
Before Nadia paints a mural, she plans what she is going to paint. She sketches the diagram shown and wants to know the measures of ∠WVX, ∠WVY, ∠XWY, and ∠YVZ.

Question 6.
Reasoning What quantities are given in the problem and what do the numbers mean? What do you know from the diagram?
Answer:
Question 7.
Make Sense and Persevere What do you need to find?
Answer:
Question 8.
Use Appropriate Tools Measure ∠WVX, ∠WVY, and ∠YVZ. What is the best tool to use?

Answer:
Question 9.
Model with Math Write and solve an equation which could be used to find the measure of ∠XVY. What is the measure of the angle?
Answer:
Topic 15 Fluency Practice Activity
Follow the path
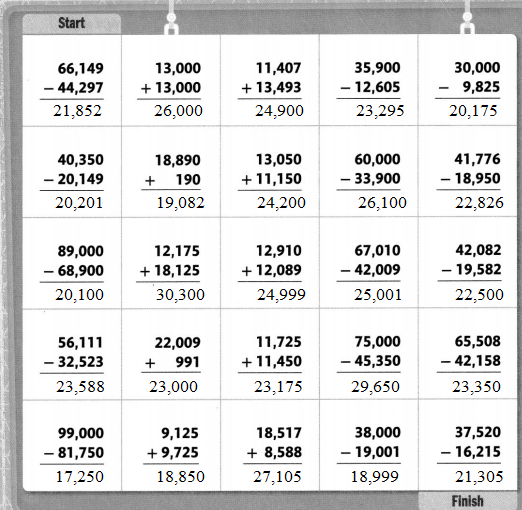
Shade a path from START to FINISH. Follow sums and differences that are between 20,000 and 25,000. You can only move up, down, right, or left.
I can … add and subtract multi-digit whole numbers.
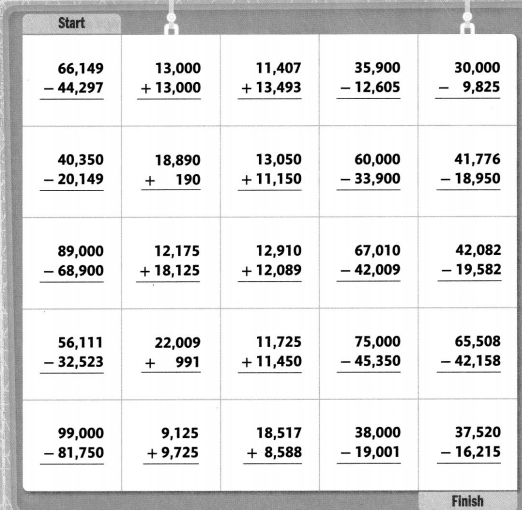
Answer:
Topic 15 Vocabulary Review
Word List
- acute angle
- angle measure
- degree (0)
- line
- line segment
- obtuse angle
- point
- protractor
- ray
- right angle
- straight angle
- unit angle
- vertex
Understand Vocabulary
Question 1.
Cross out the terms that do NOT describe an angle with a square corner.
acute angle
right angle
obtuse angle
straight angle
Answer: Straight angle.
Explanation:
We can describe acute angle, obtuse angle, right angle with a square corner. A straight angle cannot be described with a square corner.
Thus the answer is option D.
Question 2.
Cross out the terms that do NOT describe an angle open less than a right angle.
acute angle
right angle
obtuse angle
straight angle
Answer:
obtuse angle, straight angle are the terms that do NOT describe an angle open less than a right angle.
Question 3.
Cross out the terms that do NOT describe an angle that forms a straight line.
acute angle
right angle
obtuse angle
straight angle
Answer:
acute angle, right angle, obtuse angle are the terms that do NOT describe an angle that forms a straight line.
Question 4.
Cross out the terms that do NOT describe an angle open more than a right angle, but less than a straight angle.
acute angle
right angle
obtuse angle
straight angle
Answer:
acute angle, right angle and straight angle are the terms that do NOT describe an angle open more than a right angle, but less than a straight angle.
Label each example with a term from the Word List.
Question 5.
![]() ___________
___________
Answer: straight line, because it has does not have endpoints.
Question 6.
![]() ___________
___________
Answer: ray, because it has one endpoint.
Question 7.
![]() ___________
___________
Answer: line segment, because it has two endpoints.
Question 8.
 ____________
____________
Answer: 2 rays with a single endpoint
Use Vocabulary in Writing
Question 9.
Describe how to measure an angle. Use at least 3 terms from the Word List in your explanation.
Answer: We can measure an angle using a protractor, compass, and blocks.
Topic 15 Reteaching
Set A pages 549-552
A ray has one endpoint and continues on forever in one direction.
A line segment is a part of a line with two endpoints.
An angle is formed by two rays with a common endpoint.
Remember that a line segment is a part of a line.
Use geometric terms to describe what is shown.
Question 1.

Answer: line segment, because it has two endpoints.
Question 2.
Answer: right angle
Question 3.
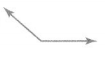
Answer: obtuse angle
Question 4.

Answer: ray, because it has one endpoint
Set B pages 553-556
The angle below is \(\frac{1}{3}\) of the circle.
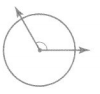
\(\frac{1}{3}\) means 1 of 3 equal parts.
360° ÷ 3 = 120°
The measure of this angle is 120°.
Remember there are 360° in a circle.
A circle is cut into eighths. What is the angle measure of each piece?
Question 1.
Use division to solve.
Answer:
Given,
A circle is cut into eighths.
360/8 = 45 degrees
90/2 = 45 degrees
Question 2.
Use multiplication to solve.
Answer:
Set C pages 557-560
You can use an angle you know to find the measure of other angles. The smaller angle of the tan pattern block has a measure of 30°
Three of the 30° angles will fit into the angle.
Add: 30° + 30° + 30o = 90°
The measure of this angle is 90°.
Remember you can use any angle that you know the measure of to find the measure of other angles.
Find the measure of each angle. Use pattern blocks.
Question 1.
Answer: 55 degrees
Question 2.

Answer: 110 degrees
Set D pages 561-564
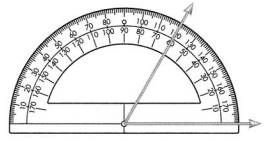
The measure of this angle is 60°.
Remember that a straight angle has a measure of 180°.
Measure the angles.
Question 1.

Answer: 90 degrees
Question 2.
Answer: 120 degrees
Set E pages 565-568
When an angle is decomposed into non-overlapping parts, the angle measure of the whole is the sum of the angle measures of the parts.
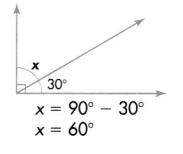
Remember you can subtract to find angle measures.
∠ABD is decomposed into two non-overlapping angles, ∠ABC and ∠CBD. Complete the table.
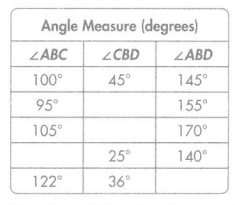
Answer:
Set F pages 569-572
Think about these questions to help you use appropriate tools strategically.
Thinking Habits
- Which tools can I use?
- Why should I use this tool to help me solve the problem?
- Is there a different tool could use?
- Am I using the tool appropriately?

Remember there may be more than one appropriate tool to use to solve a problem.
One-eighth of the pie is missing from the tin.
Question 1.
What tools can Delia use to measure the angle of the missing piece?
Answer: protractor can be used to measure the angle of the missing piece.
Question 2.
How can you calculate the measure?
Answer: We can calculate the measure of an angle using protractor.
Topic 15 Assessment Practice
Question 1.
What is the measure of the angle shown below? Name a type of angle that has an angle measure greater than the angle shown.
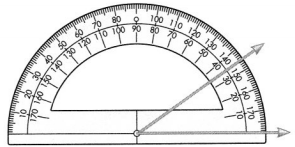
Answer:
The measure of the angle is 35 degrees.
The name of the angle is an acute angle.
Question 2.
Megan needs to find the measures of the angles on a bridge.

A. Find the measure of ∠YXW if ∠YXZ is 85° and ∠ZXW is 40°. Write and solve an addition equation.
Answer:
B. Find the measure of ∠CAD if ∠CAB is a right angle and ∠DAB is 45°. Write and solve a subtraction equation.
Answer:
Question 3.
If you divide a circle into 360 equal angles, what is the angle measure of each angle?
Answer:
you divide a circle into 360 equal angles
360 ÷ 6 = 60 degree
60 + 60 + 60 + 60 + 60 + 60
Thus the angle measure of each angle is 60 degrees.
Question 4.
Choose the correct term from the box to complete each statement.
Line Segment
Ray
A __________ has one endpoint.
A __________ has two endpoints.
Answer:
A Ray has one endpoint.
A Line segment has two endpoints.
Question 5.
Draw an example of a line \(\overleftrightarrow{R S}\). Label a point T between points Rand S. Using point T, draw ray \(\overrightarrow{T V}\).
Answer:
Question 6.
JKL is a straight angle decomposed into 2 non-overlapping angles, ∠JKM and ∠MKL. If ∠MKL measures 104°, what type of angle is ∠JKM? What is the measure of ∠JKM?
Answer:
Question 7.
∠ABC has a measure of 40°and ∠CBD has a measure of 23°. The angles share a ray and form ZABD. Write and solve an equation to find the measure of ∠ABD.
Answer: ∠ABC + ∠CBD + ∠ABD = 90°
Question 8.
Emma cuts slices from pies. Match each fraction with the equal angle measure.
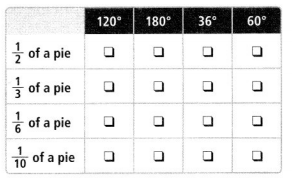
Answer:
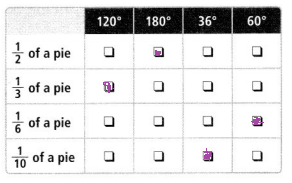
Question 9.
Select all the true statements.
☐ An acute angle is open less than a right angle.
☐ An obtuse angle makes a square corner.
☐ A right angle is open less than an obtuse angle.
☐ A straight angle forms a straight line.
☐ All obtuse angles have the same measure.
Answer:
☐ An acute angle is open less than a right angle.
☐ A right angle is open less than an obtuse angle.
☐ A straight angle forms a straight line.
Thus A, C, D are the true statements.
Question 10.
Two wooden roof beams meet at a 60° angle. Draw an angle to represent how the beams meet.
Answer:
Question 11.
Which geometric term best describes the light that shines from a flashlight?

A. Point
B. Ray
C. Line segment
D. Line
Answer: Ray
Question 12.
Terry is measuring ∠RST using pattern blocks. The smaller angle of each of the tan pattern blocks shown below measures 30°. What is the measure of ∠RST? Explain.
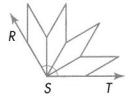
Answer:
Given,
Terry is measuring ∠RST using pattern blocks.
The smaller angle of each of the tan pattern blocks shown below measures 30°.
Thus the measure of ∠RST is 30° + 30° + 30° + 30° = 120
Question 13.
Identify an acute angle, a right angle, and an obtuse angle in the figure below.

Answer:
∠AEB is an acute angle
∠DEC is a right angle
∠BED is an obtuse angle
Topic 15 Performance Task
Ancient Roads
The ancient Romans built roads throughout their empire. Many roads were paved with stones that fit together. The spaces between the stones were filled with sand and gravel. Many of these roads still exist today, over 2,000 years after they were built.
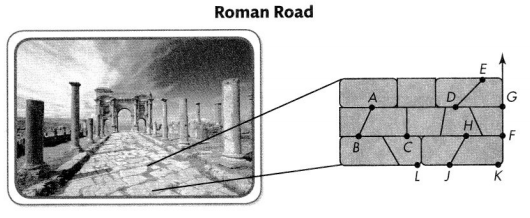
Question 1.
As seen in the Roman Road figure, the stones formed angles and geometric figures.
Part A
What geometric figure has one endpoint at F and goes on forever through point G?
Answer: E
Part B
Is ∠EDA right, acute, or obtuse? Explain.
Answer:
∠EDA is an obtuse angle.
Part C
∠EDG turns through \(\frac{1}{8}\) of a circle. What is its angle measure? Explain.
Answer:
∠EDG turns through \(\frac{1}{8}\) of a circle.
80
Question 2.
Answer the following to find the measure of ∠HJK and ∠HJL in the Measuring a Roman Road figure.
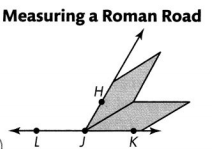
Part A
Name two tools you could use to measure the angles.
Answer: Protractor and blocks pattern could be used to measure the angles.
Part B
The smaller angle of the tan pattern block measures 30°, as shown in the Tan Pattern Block figure. A 30-degree angle is 30 one-degree angles. What is the measure of ∠HJK in the Measuring a Roman Road figure? Explain.

Answer:
Part C
What is the measure of ∠HJL in the Measuring a Roman Road figure? Write and solve an equation to find the measure of the angle.
Answer: