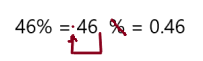
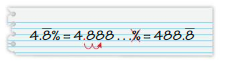
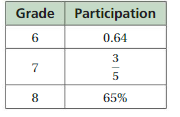
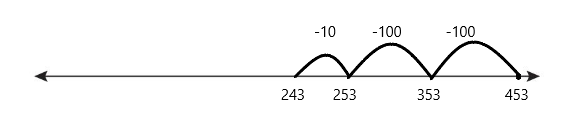
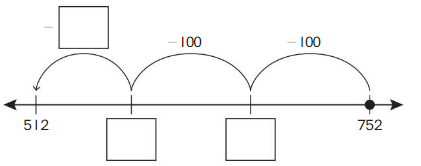
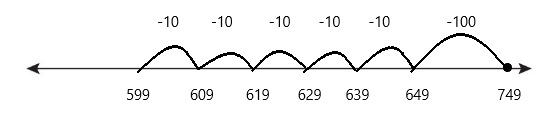
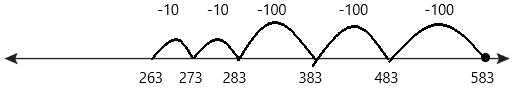
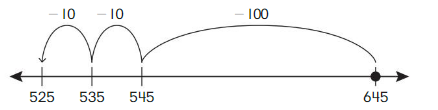
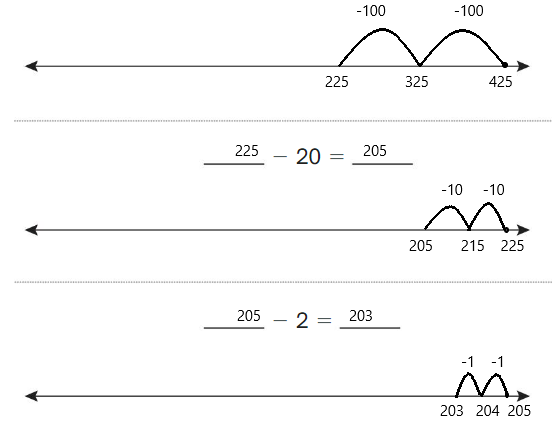
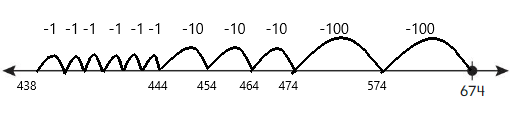
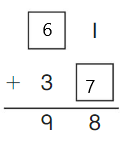
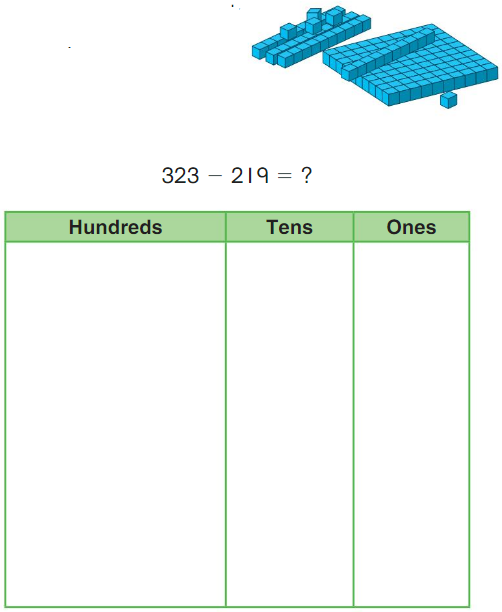
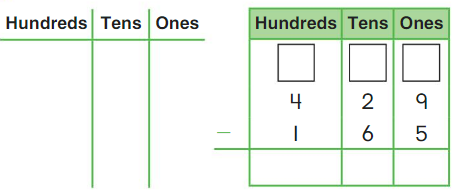
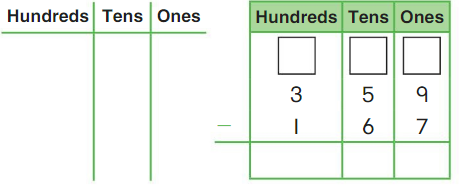
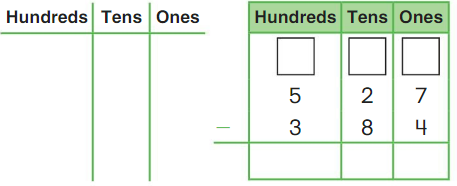
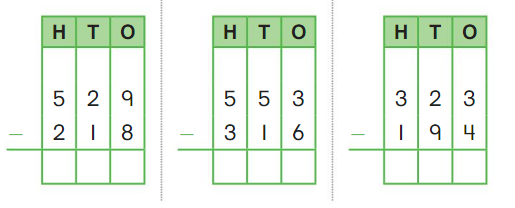
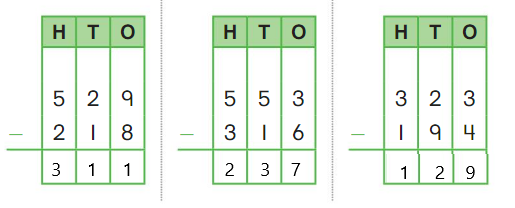
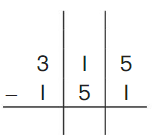
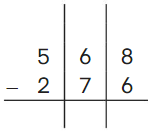
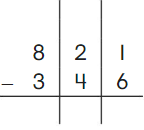
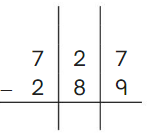
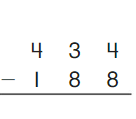
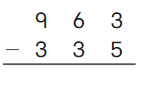
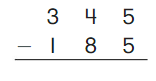
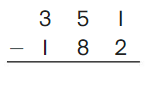
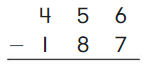
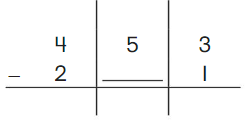
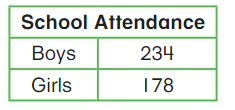
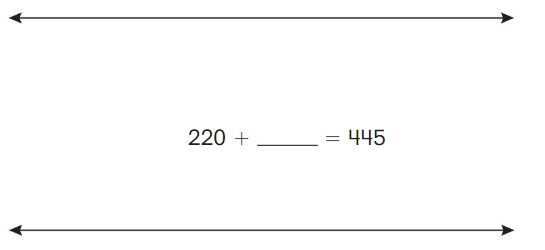
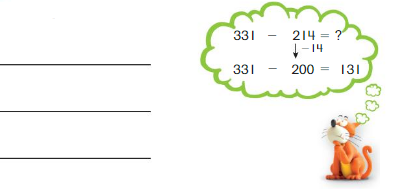
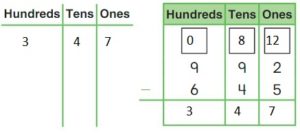
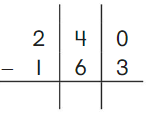
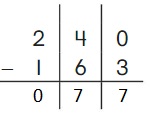
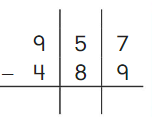
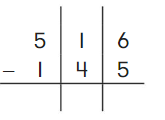
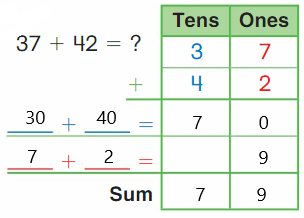
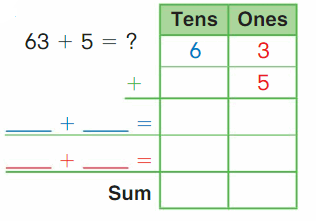
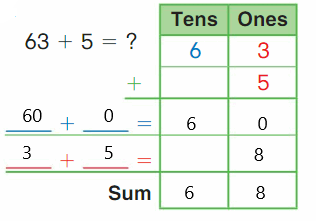
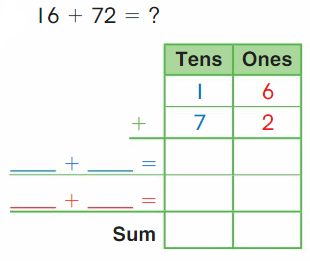
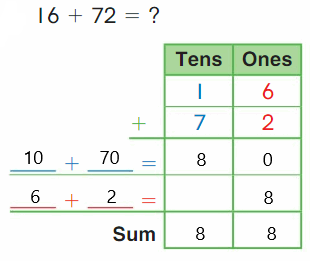
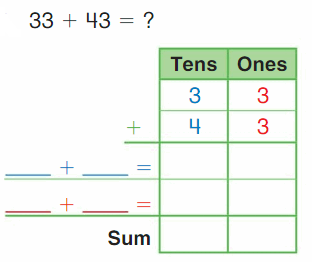
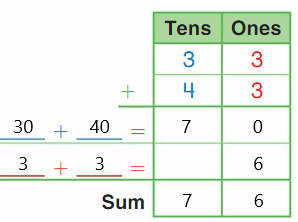
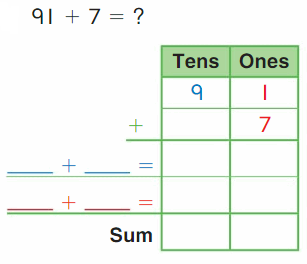
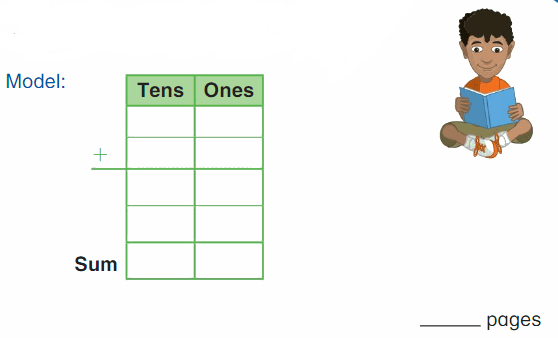
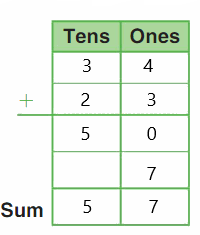
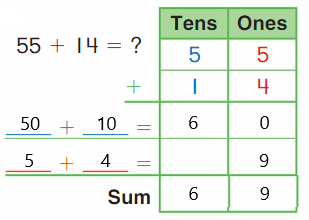
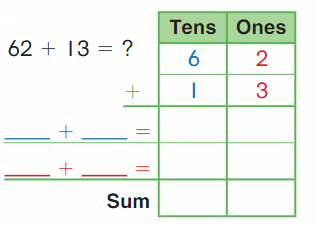
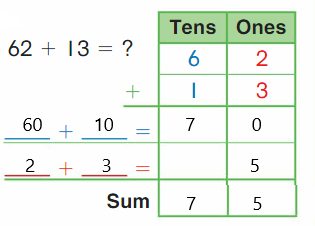
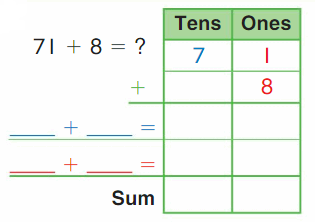
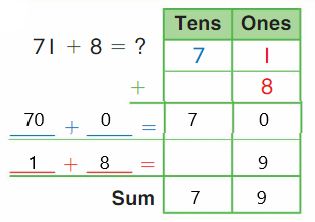
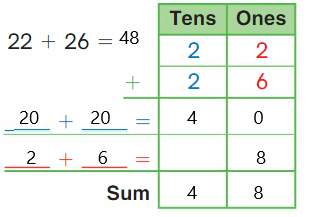
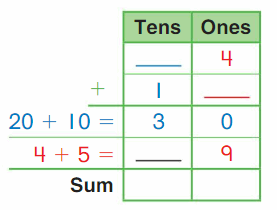
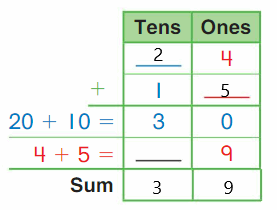
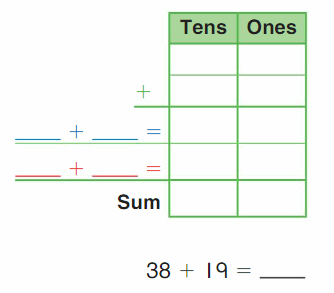
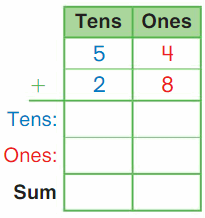
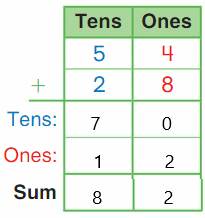
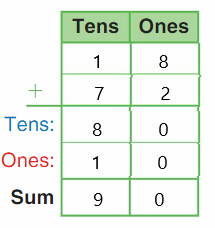
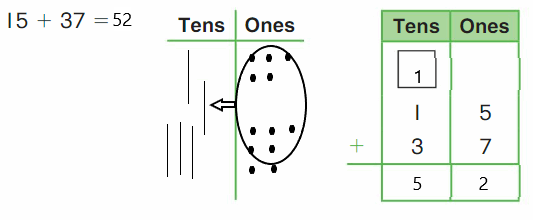
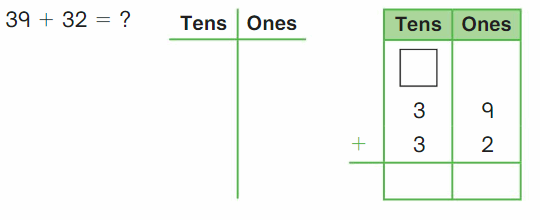
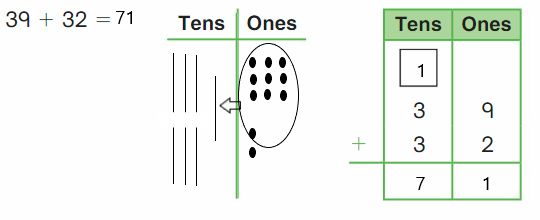
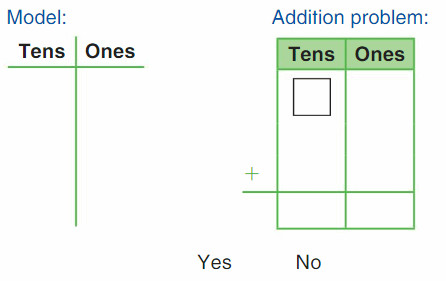
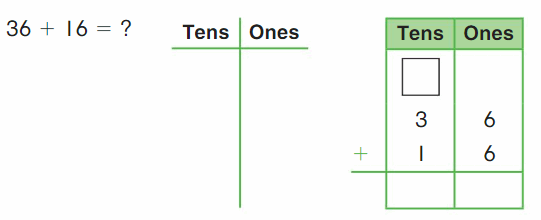
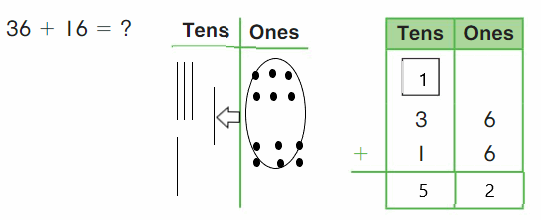
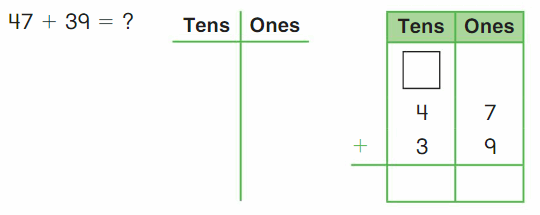
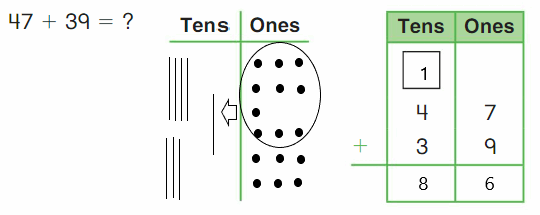
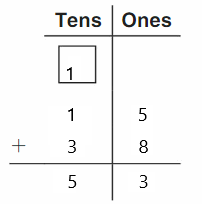
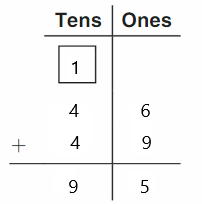
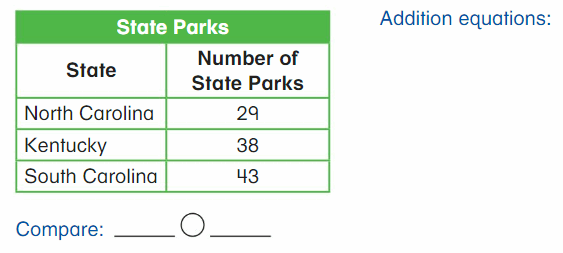
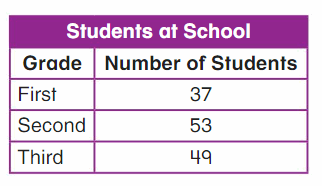
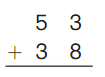
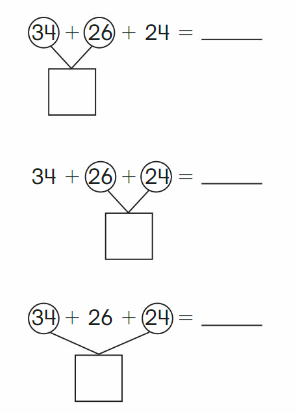
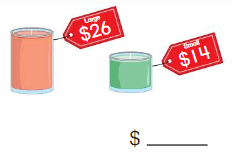
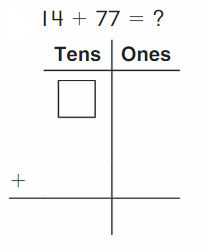
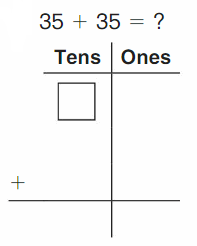
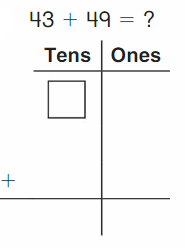
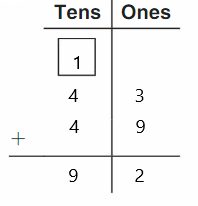
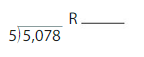
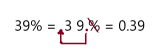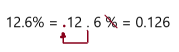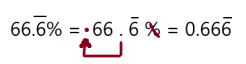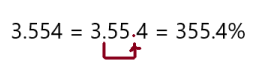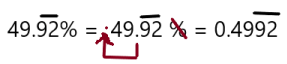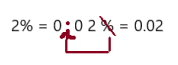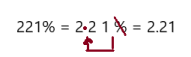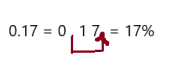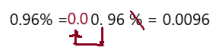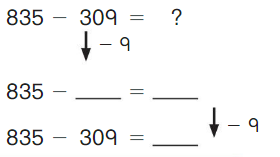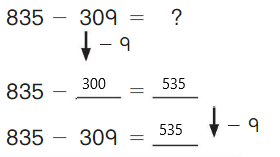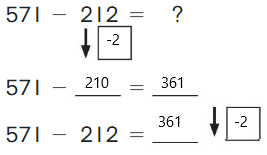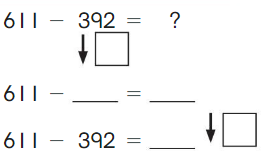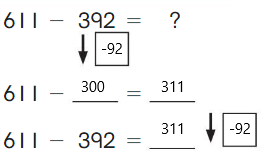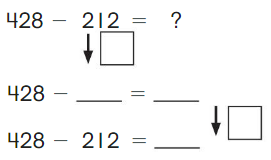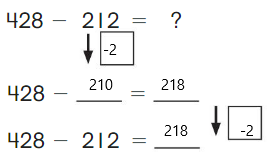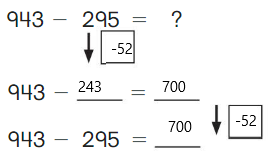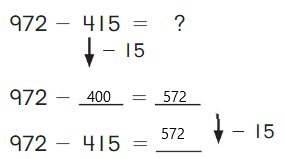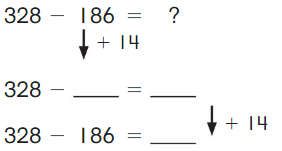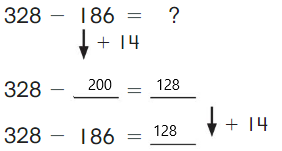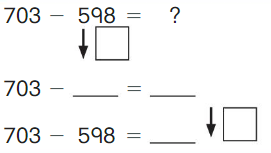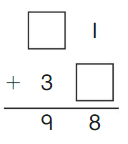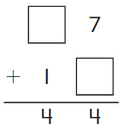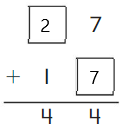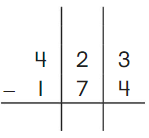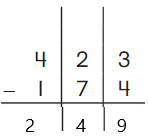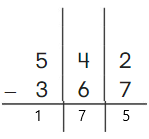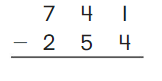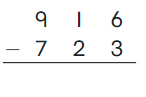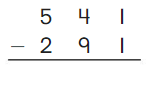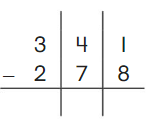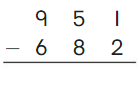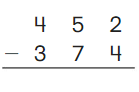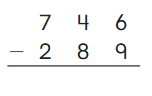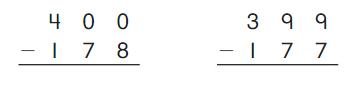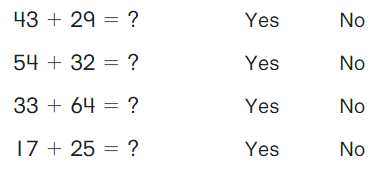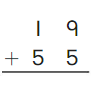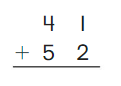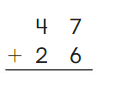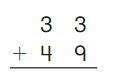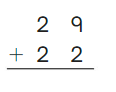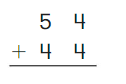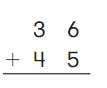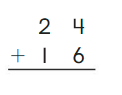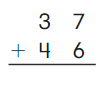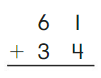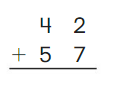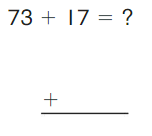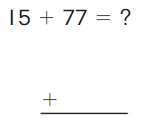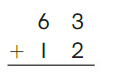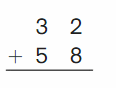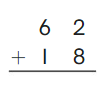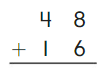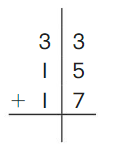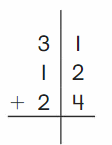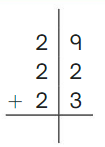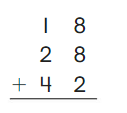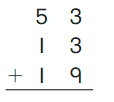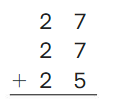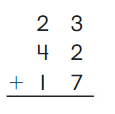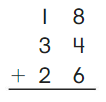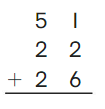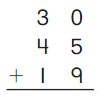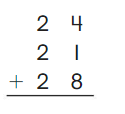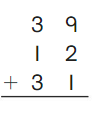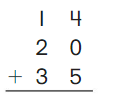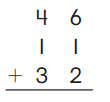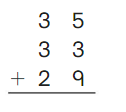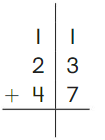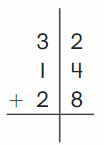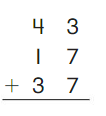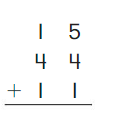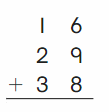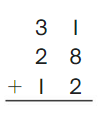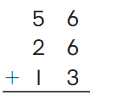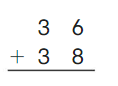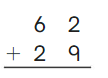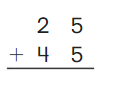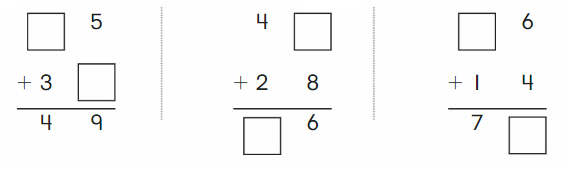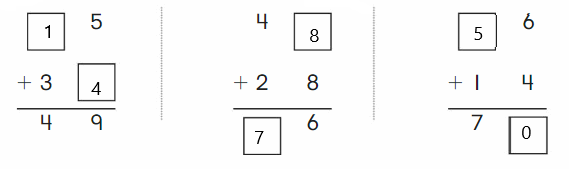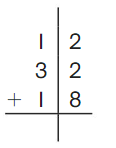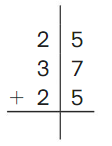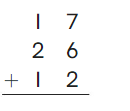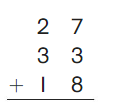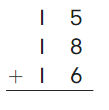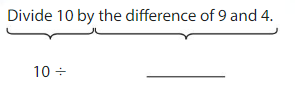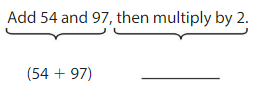Go Math Grade K Chapter 6 Answer Key Subtraction
Subtraction Show What You Know
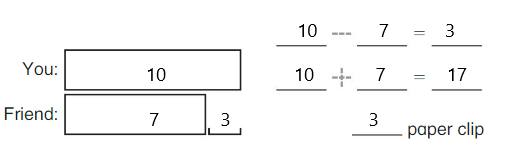
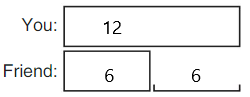
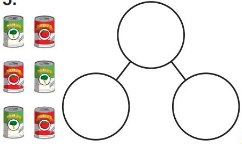
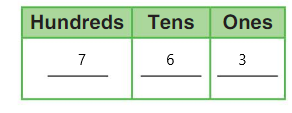
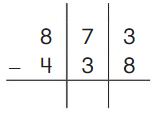
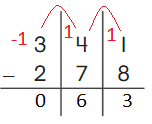
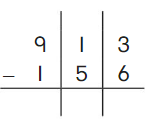
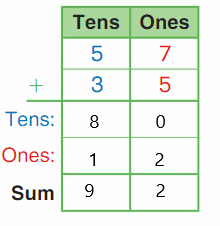
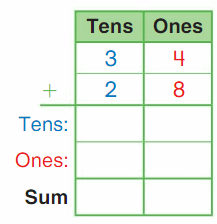
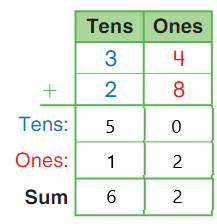
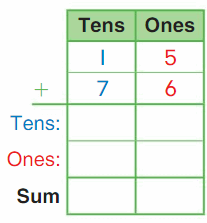
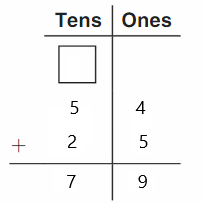
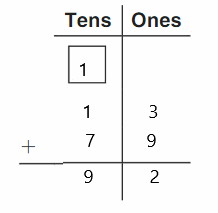
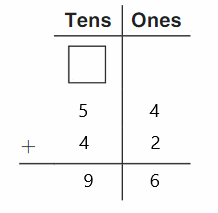
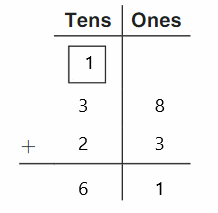
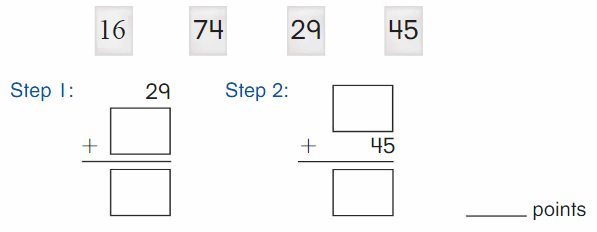
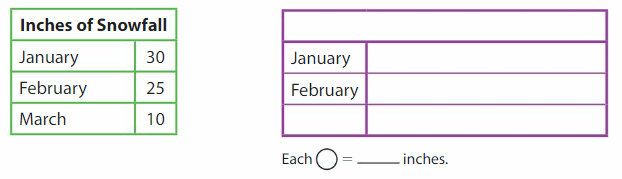
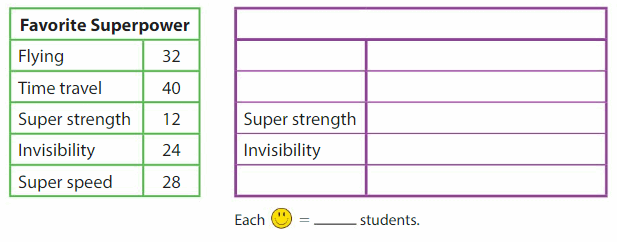
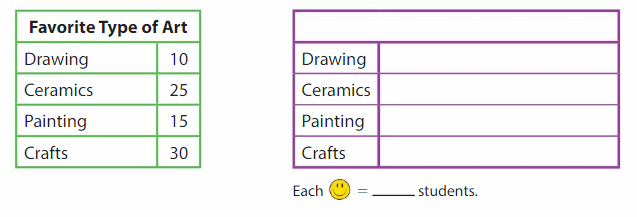
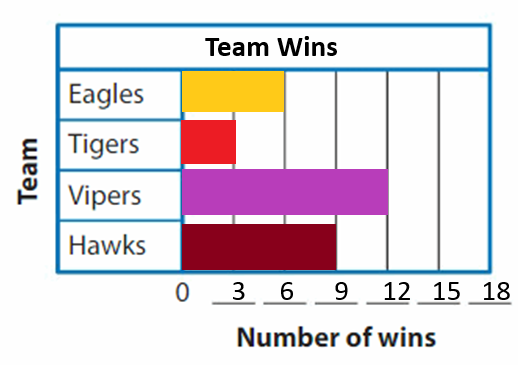
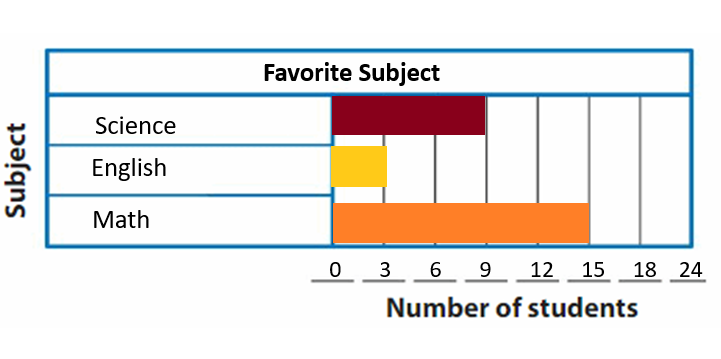
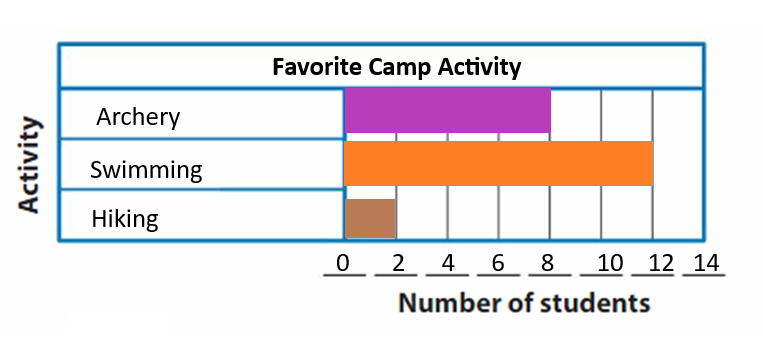
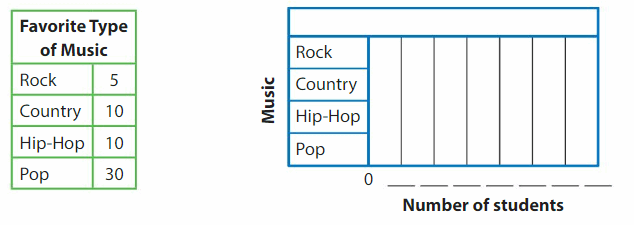
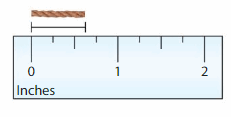
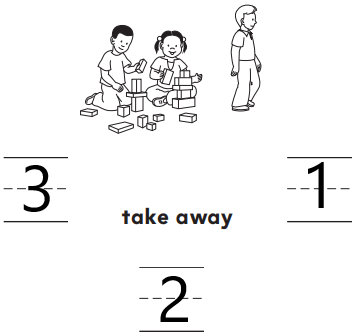
DIRECTIONS 1–2. Count and tell how many. Draw a set with one fewer counter. Write how many in each set. 3. Write the number of cubes in each set. Circle the number that is less than the other number.
Question 1.

Answer:
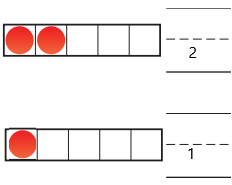
The number of counters in the first set are two and the number of counters in the second set are one.
Explanation:
In the first image, we can see that the number of counters is two. As there are two counters in the first image, given that to draw fewer counters than the first set. So we will take only one counter in the second set.
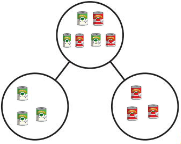
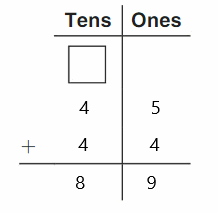
Question 2.

Answer:
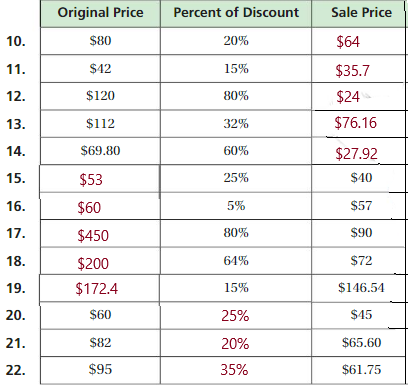
The number of counters in the first set is 4 and the number of counters in the second set is 3.
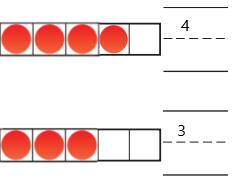
Explanation:
In the first image we can see that the number of counters is 4. As there are four counters in the first image, given that to draw fewer counters than the first set. So we will take only three counters in the second image.
Compare Numbers to 10
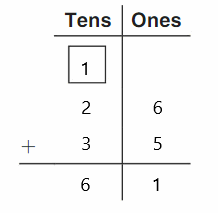
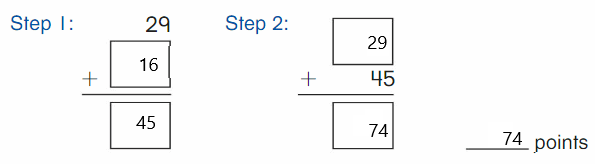
Question 3.

Answer:
The number of cubes in first set is 7 and the number of cubes in second set is 4.
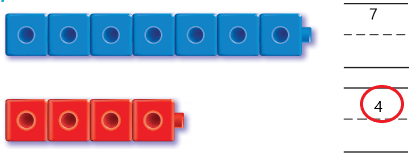
Explanation:
In the above image, we can see two types of sets. The first set contains seven cubes which are in blue color and the second set contains four cubes which are in red color. So we have to circle it for less number which is four.
Subtraction Vocabulary Builder
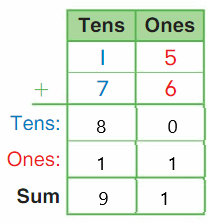
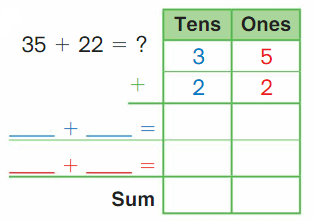
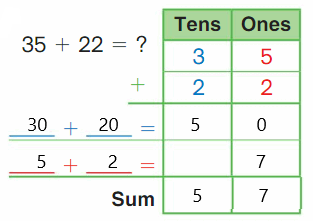
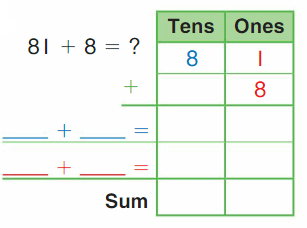
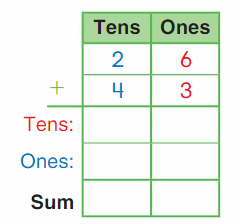
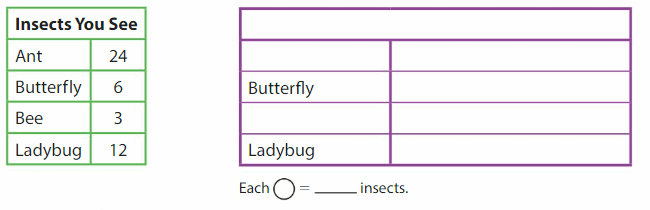
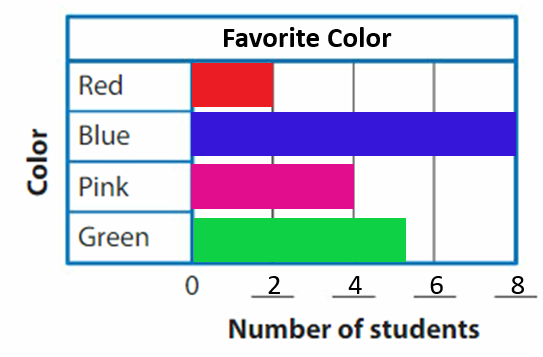
DIRECTIONS Add the set of bees and the set of butterflies. Write how many insects altogether.

Answer:
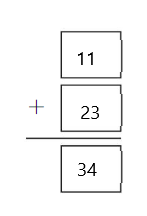
The sum of the set of bees and the set of butterflies is 10.
Explanation:
The set of bees are five and the set of butterflies are five. Here we performed addition to know the insects altogether and the sum can be defined as the resulting of two or more numbers by adding. So here the sum of the set of bees and the set of butterflies is
5 + 5 is 10.

Subtraction Game Spin for More
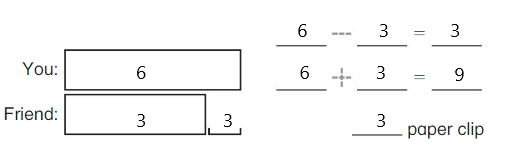
DIRECTIONS Play with a partner. Decide who goes first. Take turns spinning to get a number from each spinner. Use cubes to model a cube train with the number from the first spin. Say the number. Add the cubes from the second spin. Compare your number with your partner’s. Mark an X on the table for the player who has the greater number. The first player to have five Xs wins the game.
MATERIALS two paper clips, connecting cubes

Subtraction Vocabulary Game
DIRECTIONS Players take turns. A player chooses a secret word from the Word Box and then sets the timer. The player draws pictures to give hints about the secret word. If the other player guesses the secret word before time runs out, he or she puts a counter in the chart. The first player who has counters in all his or her boxes is the winner.
MATERIALS timer, drawing paper, two-color counters for each player

The Write Way
DIRECTIONS Draw to show how to solve a subtraction problem. Write a subtraction sentence. Reflect Be ready to tell about your drawing.

Lesson 6.1 Subtraction: Take From
Essential Question How can you show subtraction as taking from?
Share and Show
DIRECTIONS 1. Listen to the subtraction word problem. Trace the number that shows how many children in all. Write the number that shows how many children are leaving. Write the number that shows how many children are left.
Question 1.

Answer:

Explanation:
In the above image, we can see that there are four children and two children are leaving. So here we will subtraction
The number that shows how many children in all are four by observing the above image. The number that shows how many children are leaving are two. The number that shows how many children left are two.
DIRECTIONS 2. Listen to the subtraction word problem. Write the number that shows how many children in all. Write the number that shows how many children are leaving. Write the number that shows how many children are left.
Question 2.

Answer:

Explanation:
The total number of children is five by observing the above image. The number that shows how many children are leaving is one. The number that shows how many children left are four.
Problem Solving • Applications
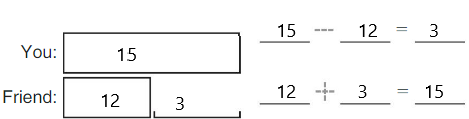
DIRECTIONS 3. Blair has two marbles. His friend takes one marble from him. Draw to show the subtraction. Write the numbers. 4. Write the number that shows how many marbles Blair has now.
Question 3.

Answer:


Explanation:
Blair has two marbles by observing the above image. His friend takes one marble from him. Subtract one marble from total number of marbles. So number of marbles left over are one.
Question 4.
_________
_ _ _ _ _ _ _
_________
Answer:

Explanation:
Blair has one marble as his friend has one marble from the two marbles he has.
HOME ACTIVITY • Show your child a set of four small objects. Have him or her tell how many objects there are. Take one of the objects from the set. Have him or her tell you how many objects there are now.
Subtraction: Take From Homework & Practice 6.1
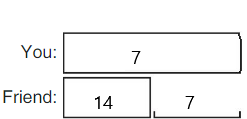
DIRECTIONS 1. Tell a subtraction word problem about the children. Write the number that shows how many children in all. Write the number that shows how many children are leaving. Write the number that shows how many children are left.
Question 1.

Answer:
Explanation:
The number that shows how many children in all are three by observing the above image. The number that shows how many children are leaving is one. The number that shows how many children left are two.
DIRECTIONS 1. Tell a subtraction word problem about the frogs. Write the number that shows how many frogs are left. 2. Tell an addition word problem about the birds. Write and trace to complete the addition sentence. 3. How many more counters would you place to model a way to make 8? Draw the counters.
Lesson Check
Question 1.

Answer:

Explanation:
The total number of frogs are three and one is taken away. The number that shows how many frogs left are two by observing the above image. So leftover frogs are two.
Spiral Review
Question 2.

Answer:
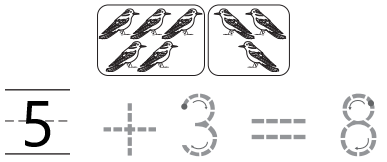
Explanation:
In the above image, we can see two boxes. The first box contains five birds and the second box contains three birds. By adding birds in these two boxes results in the total number of birds. The total number of birds is eight.
Question 3.

Answer:
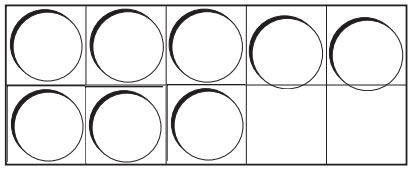
Explanation:
In the given image, we can see five counters are present.
In order to model a way to make counters eight, three more counters need to be added. So, we have to place three more counters to model a way to make eight counters.
Lesson 6.2 Subtraction: Take Apart
Essential Question How can you show subtraction as taking apart?
Listen and Draw
DIRECTIONS Listen to the subtraction word problem. Place seven counters in the ten frame as shown. Trace the counters. Trace the number that shows how many in all. Trace the number that shows how many are red. Write the number that shows how many are yellow.

Answer:
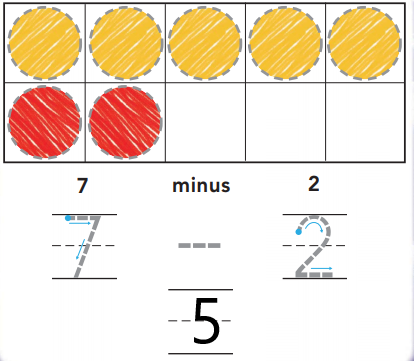
Explanation:
We have to place seven counters in the ten frames as shown in the above image. The number that shows the total number of counters in all is seven. The number that shows the number of counters in red is two. The number of yellow counters is obtained by subtracting red counters from the total number of counters. Thus, we have five yellow counters.
Share and Show
DIRECTIONS 1. Listen to the subtraction word problem. Place eight counters in the ten frame. Draw and color the counters. Trace the number that shows how many in all. Write the number that shows how many are yellow. Write the number that shows how many are red.
Question 1.

Answer:
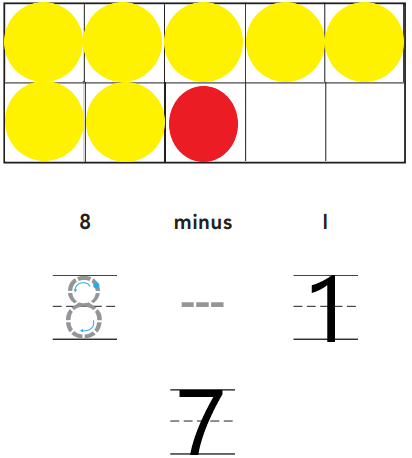
Explanation:
Place eight counters in the ten frames as shown in the above figure. The number of red counters is one. By subtracting the number of red counters from the total number of counters, we will get the number of yellow counters as seven.
DIRECTIONS 2. Listen to the subtraction word problem. Place ten counters in the ten frame. Draw and color the counters. Write the number that shows how many in all. Write the number that shows how many are red. Write the number that shows how many are yellow.
Question 2.

Answer:
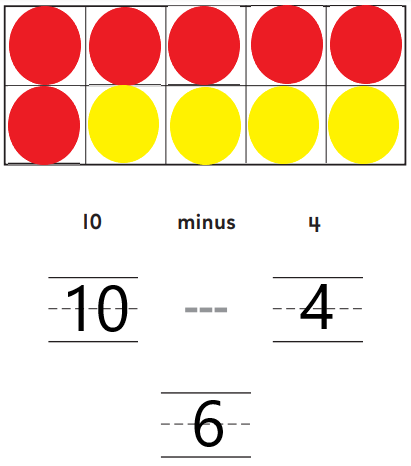
Explanation:
Place ten counters in the ten frames as shown in the above figure. The total number of yellow counters is four. By subtracting the number of yellow counters from the total number of counters will give us the number of red counters as six.
Problem Solving • Applications
DIRECTIONS 3. Juanita has nine apples. One apple is red. The rest of the apples are yellow. Draw the apples. Write the numbers and trace the symbol. 4. Write the number that shows how many apples are yellow.
Question 3.

Answer:


Explanation:
Juanita has nine apples. One apple is red. If we subtract one red apple from the total number of apples, then we will get the rest of the apples which are yellow in color are 8.
Question 4.
__________
_ _ _ _ _ _ _
__________
Answer:
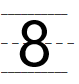
Explanation:
The total number of yellow apples are eight.
HOME ACTIVITY • Show your child a set of seven small objects. Now take away four objects. Have him or her tell a subtraction word problem about the objects.
Subtraction: Take Apart Homework & Practice 6.2
DIRECTIONS 1. Listen to the subtraction word problem. Jane has nine counters. Three of her counters are red. The rest of her counters are yellow. How many are yellow? Place nine counters in the ten frame. Draw and color the counters. Write the number that shows how many in all. Write the number that shows how many are red. Write the number that shows how many are yellow.
Question 1.

Answer:
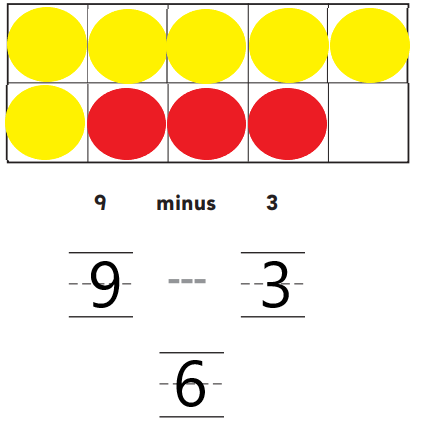
Explanation:
Jane has nine counters as shown in the above image. Three of her counters are red. The rest of her counters are yellow. We placed nine counters in the ten frames and colored the counters. The number that shows how many in all are nine. The number that shows how many are red is three. Subtract three red counters from the total number of counters to get the number of yellow counters. The number of yellow counters is six.
DIRECTIONS 1. Clyde has eight counters. Two of his counters are yellow. The rest of his counters are red. How many are red? Draw and color the counters. Write the number that shows how many are red. 2. Count the number of leaves in each set. Circle the set that has the greater number of leaves. 3. Compare the cube trains. Write how many. Circle the number that is greater.
Lesson Check
Question 1.

Answer:
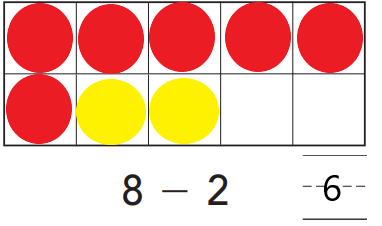
Explanation:
Clyde has eight counters by observing the above image. Two of his counters are yellow. The rest of his counters are red. In order to get the number of red counters, we have to subtract yellow counters from the total number of counters. So, the number of red counters is six.
Spiral Review
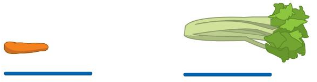
Question 2.

Answer:

Explanation:
In the above image, we can see the number of leaves in the first set is four. The number of leaves in the second set is five. So circle the set that has the greater number of leaves. The second set contains a greater number of leaves. So, circle for the second set.
Question 3.

Answer:
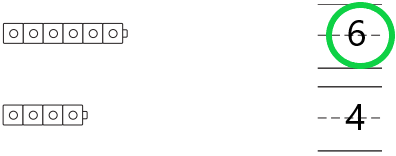
Explanation:
In the above image, we can see two cube trains. The total number of cubes in the first train is six and the total number of cubes in the second train is four. By Comparing these two cube trains, circle for the number that is greater. So we have to circle for the first train which has a greater number of cubes in it.
Lesson 6.3 Problem Solving • Act Out Subtraction Problems
Essential Question How can you solve problems using the strategy act it out?
Try Another Problem
DIRECTIONS 1. Listen to and act out the subtraction word problem. Trace the numbers and the symbols. Write the number that shows how many children are left.
Question 1.

Answer:

Explanation :
Total two children are there in the above image. One child left the place and another child remains there in the same place. Subtract total number of child left from total number of child. So, only one child leftover at that place.
Share and Show
DIRECTIONS 2. Listen to and act out the subtraction word problem. Trace the numbers and the symbols. Write the number that shows how many children are left.
Question 2.

Answer:

Explanation:
The total number of children in the above image is four. Two children left the place and two children remain in the same place. So, the number of children leftover is two.
On Your Own
DIRECTIONS 3. Tell a subtraction word problem about the kittens. Trace the numbers and the symbols. Write the number that shows how many kittens are left. 4. Draw to show what you know about the subtraction sentence. Write how many are left. Tell a friend a subtraction word problem to match.
Question 3.

Answer:
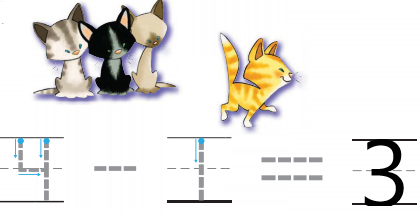
Explanation:
In the above image, we can see four kittens. One kitten left the place and some kittens remain in the same place. Subtract number of kitten left from the total number of kittens .So, the number of kittens leftover is three.
Question 4.

Answer:

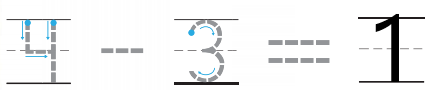
Explanation:
The total number of flowers in the above image is four. Three flowers are taken away from the place and one flower remains in the same place. In order to get the left over flowers we have subtract total number of flowers taken away from the total number of flowers. So the number of flowers leftover is one.
HOME ACTIVITY • Tell your child a short subtraction word problem. Have him or her use objects to act out the word problem.
Problem Solving • Act Out Subtraction Problems Homework & Practice 6.3
DIRECTIONS 1. Tell a subtraction word problem about the beavers. Trace the numbers and the symbols. Write the number that shows how many beavers are left. 2. Draw to tell a story about the subtraction sentence. Write how many are left. Tell a friend about your drawing.
Question 1.

Answer:
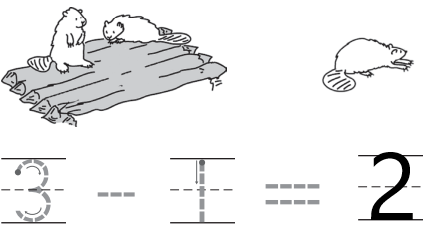
Explanation:
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. In the above image we can see the total number of beavers are three. One beaver left the place and two beavers remains in the same place. So, the number of beavers leftover are two.
Question 2.

Answer:


Explanation:
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. The result of a subtraction is called a difference. In the above image we can see four penguins. Three penguins left the place and one penguin remains in the same place.
DIRECTIONS 1. Tell a subtraction word problem about the birds. Trace the numbers and the symbols. Write the number that shows how many birds are left. 2. Count and tell how many bees. Write the number. 3. How many more counters would you place to model a way to make 7? Draw the counters.
Lesson Check
Question 1.

Answer:
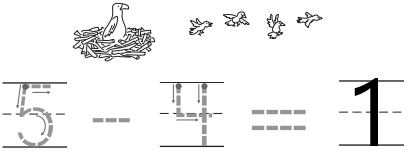
Explanation:
The process of taking one number or amount away from another number is called as subtraction. In the above image we can observe the total number of birds are five. Four birds left the place and one bird remains in the same place.
Spiral Review
Question 2.

Answer:

Explanation:
In the above image, we can see a group of bees. The addition is taking two or more numbers and adding them together. The total number of bees are nine.
Question 3.

Answer:
Explanation:
Four more counters are needed to place the model in a way to make seven. The addition is taking two or more numbers and adding them together. In the above image we can observe Four counters are added.
Lesson 6.4 Algebra • Model and Draw Subtraction Problems
Essential Question How can you use objects and drawings to solve subtraction word problems?
Share and Show
DIRECTIONS 1. Model a four-cube train. One cube is blue and the rest are green. Take apart the train to show how many cubes are green. Draw and color the cube trains. Trace and write to complete the subtraction sentence. 2. Model a three-cube train. Two cubes are orange and the rest are blue. Take apart the train to show how many cubes are blue. Draw and color the cube trains. Trace and write to complete the
Question 1.

Answer:
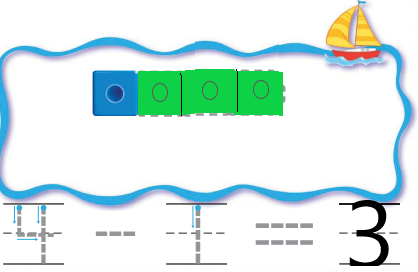
Explanation:
In the above image we can see a four-cube train. One cube is blue and the rest are green. The number of green cubes are three. Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. Here the collections has four cubes and we are removing one object(blue cube). So the remaining green cubes are three.
Question 2.

Answer:
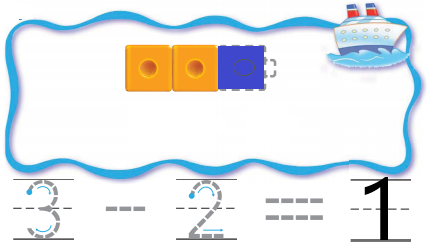
Explanation:
In the above image, we can see a three-cube train. Two cubes are orange and the rest are blue. In order to get the number of blue cubes we have to subtract two orange cubes from total number of cubes. So we got the total number of blue cubes are one.
DIRECTIONS 3. Model a four-cube train. Three cubes are red and the rest are blue. Take apart the train to show how many cubes are blue. Draw and color the cube trains. Trace and write to complete the subtraction sentence. 4. Model a five-cube train. Three cubes are yellow and the rest are green. Take apart the train to show how many cubes are green. Draw and color the cube trains. Trace and write to complete the subtraction sentence.
Question 3.

Answer:
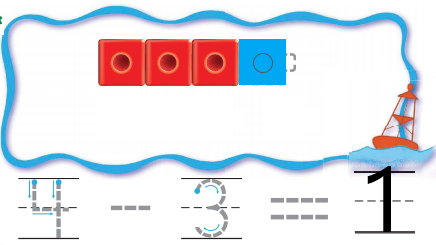
Explanation:
In the above image, we can see a four-cube train. Three cubes are red and the rest are blue. In order to get the number of blue cubes we have to subtract three red cubes from total number of cubes. So we got the total number of blue cubes are one.
Question 4.

Answer:
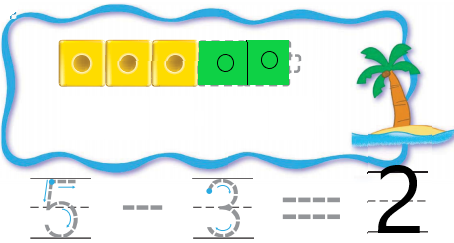
Explanation:
In the above image, we can see a five-cube train. Three cubes are yellow and the rest are green. In order to get the number of green cubes we have to subtract three yellow cubes from total number of cubes. So we got the total number of green cubes are two.
HOME ACTIVITY • Show your child two small objects. Take apart the set of objects. Have him or her tell a word problem to match the subtraction.
Algebra • Model and Draw Subtraction Problems Homework & Practice 6.4
DIRECTIONS 1. Model a three-cube train. Two cubes are red and the rest are blue. Take apart the cube train to show how many cubes are blue. Draw and color the cube trains. Trace and write to complete the subtraction sentence. 2. Model a five-cube train. One cube is yellow and the rest are green. Take apart the train to show how many cubes are green. Draw and color the cube trains. Trace and write to complete the subtraction sentence.
Question 1.

Answer:
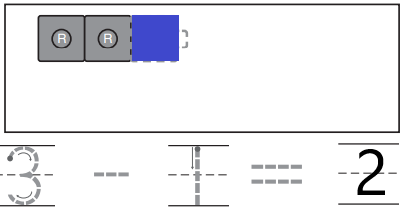
Explanation:
In the above image, we can observe a three-cube train. Two cubes are red and the rest are blue. In order to get the number of blue cubes we have to subtract two red cubes from total number of cubes. So we got the total number of blue cubes are one.
Question 2.

Answer:
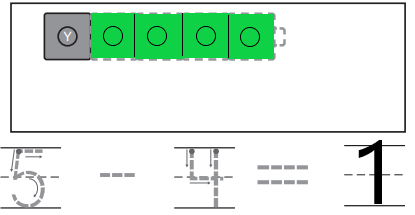
Explanation:
In the above image, we can observe a five-cube train. One cube is yellow and the rest are green. In order to get the number of green cubes we have to subtract one yellow cube from total number of cubes. So we got the total number of green cubes are four.
DIRECTIONS 1. Ellie makes the cube train shown. She takes the cube train apart to show how many cubes are gray. Trace and write to show the subtraction sentence for Ellie’s cube train. 2. Count the dots in the ten frames. Begin with 5. Write the numbers in order as you count forward. 3. Complete the addition sentence to show the numbers that match the cube train.
Lesson Check
Question 1.

Answer:

Explanation:
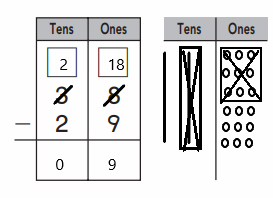
There are total five cubes in the train shown. In those some are colored gray. We need to separate total cube train into two parts to know how many cubes are gray. Substract the number of non-gray colored cubes from the total number of cubes to get the number of gray colored cubes. So, if we substract three from total five cubes, then the total number of gray colored cubes are two.
- Spiral Review
Question 2.

Answer:
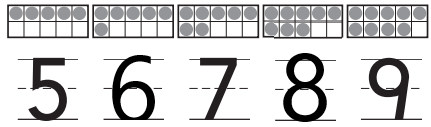
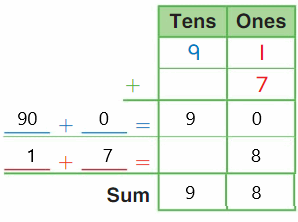
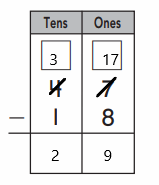
Explanation: - In the first frame, we can see that there are total ten number of counters and five are not colored grey. If we substract the number of non-colored counters from total number of counters, then we will get the total number of grey colored counters. So, substracting five from the total ten counters gives us five grey colored counters.
- Similar to the first frame, if we see in the second frame, there are total ten number of counters and four are not colored grey. If we substract the number of non-colored counters from total number of counters, then we will get the total number of grey colored counters. So, substracting four from the total ten counters gives us six grey colored counters.
- For the third frame, the same logic will apply here as well an substracting three from ten gives us seven grey colored counters.
- For the fourth frame, substracting two from the total ten counters will give us eight grey colored counters.
- For the fifth frame, substracting one from the total ten counters will give us nine grey colored counters.
Question 3.

Answer:
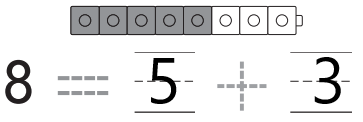
Explanation:
In the above image we can see five grey cubes and three white cubes .Perform addition to get total number of cubes. An addition sentence is a mathematical expression that shows two or more values added together and their sum. ADD five black cubes with three white cubes then we get total number of cubes. The total number of cubes are eight.
Subtraction Mid-Chapter Checkpoint
Concepts and Skills
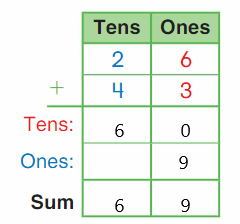
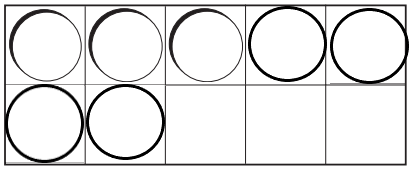
DIRECTIONS 1. Listen to the subtraction word problem. Draw and color the six circles in the ten frame. Write the number that shows how many in all. Write the number that shows how many are yellow. (K.OA.A.1) 2. Model a five-cube train. Four cubes are blue and the rest are orange. Take apart the cube train to show how many are orange. Draw and color the cube trains. Trace and write to complete the subtraction sentence. (K.OA.A.5) 3. Choose Yes or No. Does the subtraction sentence match the model? (K.OA.A.5)
Question 1.

Answer:
Explanation:
Question 2.

Answer:

Explanation:
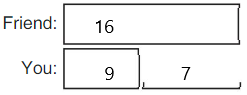
In the above image, we can observe a five-cube train. In that four cubes are blue and the rest are orange. The process of taking one number or amount away from another number is called as subtraction. We have subtract total number of blue cubes from a five cube train .Then we get total number of orange cubes. The total number of orange cube is one.
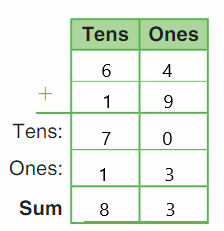
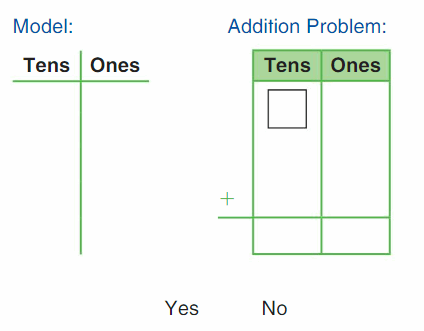
Question 3.
THINK SMARTER+

Answer:

Explanation:
In the above image, we can see a four cube train. In that, one is red cube and three are blue cubes. We have to choose the correct answer for number of red cubes by subtracting the number of blue cubes from total number of cubes. If the answer matches with the number of red cubes, then the answer is ‘Yes’ or else ‘No’.
- In the first number sentence, subtracting two blue cubes from the total four cubes will not give the correct number of red cubes. The answer doesn’t match with the number of red cubes and so the answer is ‘No’.
- In the second number sentence, substracting three blue cubes from the total four cubes equals to one red cube. So, the answer is ‘Yes’.
- In the third number sentence, substracting one blue cube from three cubes will not give correct number of red cubes. So the answer is ‘No’.
Lesson 6.5 Algebra • Write Subtraction Sentences
Essential Question How can you solve subtraction word problems and complete the equation?
Share and Show
DIRECTIONS 1. Listen to the subtraction word problem. Trace the circle and X to show how many are being taken from the set. Trace to complete the subtraction sentence. 2–3. Listen to the subtraction word problem. How many are being taken from the set? Circle and mark an X to show how many are being taken from the set. Trace and write to complete the subtraction sentence.
Question 1.

Answer:
Explanation:
In the above image we can see five scorpions. In that two scorpions are taken away from the set. Circle the scorpions that are taken away from the set and marked with X. In order to get the left over scorpions we have to subtract two scorpions from four scorpions. Then we will get the number of scorpions left over. The left over scorpion is one.
Question 2.

Answer:
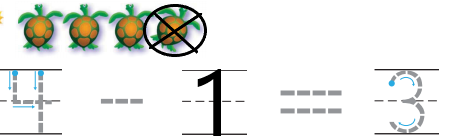
Explanation:
In the above image we can see four tortoises. In that one tortoise is taken away from the set. Circle the tortoises that are taken away from the set and marked with X. In order to get the left over tortoises we have to subtract one tortoise from four tortoises. Then we will get the number of tortoises left over. The left over tortoises are three.
Question 3.

Answer:
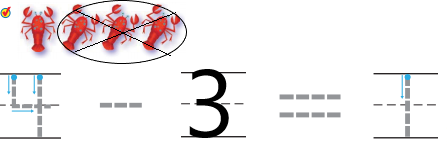
Explanation:
In the above image we can see four scorpions. In that three scorpions are taken away from the set. Circle the scorpions that are taken away from the set and marked with X. In order to get the left over scorpions we have to subtract three scorpions from four scorpions. Then we will get the number of scorpions left over. The left over scorpion is one.
DIRECTIONS 4–6. Listen to the subtraction word problem. How many are being taken from the set? Circle and mark an X to show how many are being taken from the set. Trace and write to complete the subtraction sentence.
Question 4.

Answer:
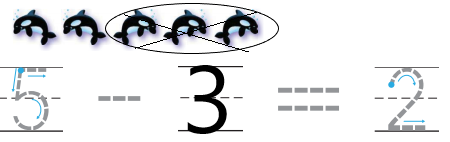
Explanation:
In the above image we can see five fish. In that three fish are taken away from the set. Circle the fish that are taken away from the set and marked with X. In order to get the left over fish we have to subtract three fish from five fish that we have, and we will get the number of fish left over. The left over fish are two as shown in the above image.
Question 5.

Answer:
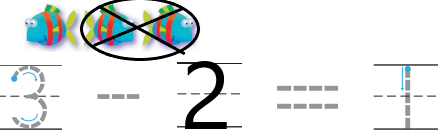
Explanation:
In the above image we can see three fish. In that two fish are taken away from the set. Circle the fish that are taken away from the set and marked with X. In order to get the left over fish we have to subtract two fish from three fish that we have, and we will get the number of fish left over. The left over fish is one.
Question 6.

Answer:
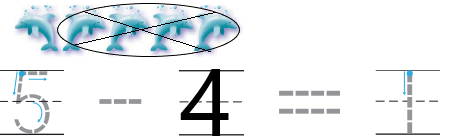
Explanation:
In the above image we can see five fish. In that four fish are taken away from the set. Circle the fish that are taken away from the set and marked with X. In order to get the left over fish we have to subtract four fish from five fish that we have, and we will get the number of fish left over. The left over fish are one as shown in the above image.
Problem Solving • Applications
DIRECTIONS 7. Kristen has four flowers. She gives her friend some flowers. Now Kristen has two flowers. How many did Kristen give her friend? Draw to solve the problem. Complete the subtraction sentence. 8. Tell a different subtraction word problem about the flowers. Draw to solve the problem. Tell a friend about your drawing. Complete the subtraction sentence.
Question 7.

Answer:


Explanation:
Kristen has four flowers as shown in the above image. She gave some flowers to her friend. Subtract two flowers from total number of flowers which are four. Now Kristen has two flowers. Kristen gave two flowers to her friend.
Question 8.

Answer:

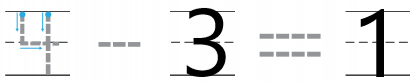
Explanation:
The total number of flowers in the above image are four. Three flowers are taken away from the place and one flower remains in the same place. In order to get the left over flowers we have subtract total number of flowers taken away from the total number of flowers. So the number of flowers leftover is one.
HOME ACTIVITY • Have your child draw a set of five or fewer balloons. Have him or her circle and mark an X on some balloons to show that they have popped. Then have your child tell a word problem to match the subtraction.
Algebra • Write Subtraction Sentences Homework & Practice 6.5
DIRECTIONS 1–3. Listen to the subtraction word problem about the animals. There are _____ _____. _____ are taken from the set. Now there are ____. How many are taken from the set? Circle and mark an X to show how many are being taken from the set. Trace and write to complete the subtraction sentence.
Question 1.

Answer:
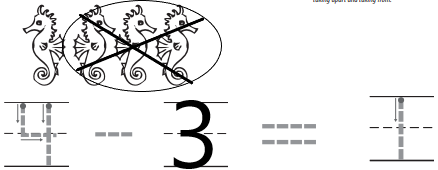
Explanation:
In the above image we can see four animals. In that three animals are taken away from the set. Circle the animals that are taken away from the set and marked with X. In order to get the left over animals we have to subtract three animals from total number of animals. Then we will get the number of animals left over. The left over animal is one.
Question 2.

Answer:
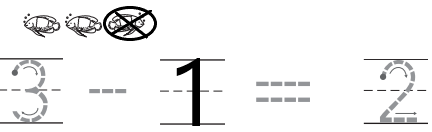
Explanation:
In the above image we can see three animals. In that one animal is taken away from the set. Circle the animals that are taken away from the set and marked with X. In order to get the left over animals we have to subtract one animal from total number of animals. Then we will get the number of animals left over. The left over animals are two.
Question 3.

Answer:
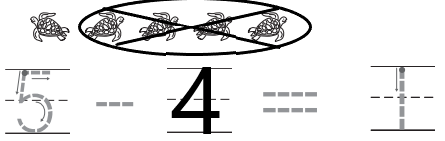
Explanation:
In the above image we can see five animals. In that four animals are taken away from the set. Circle the animals that are taken away from the set and marked with X. In order to get the left over animals we have to subtract four animals from total number of animals. Then we will get the number of animals left over. The left over animal is one.
DIRECTIONS 1. Trace and write to show the subtraction sentence for the set. 2. Count the number of counters in each set. Circle the set that has the greater number of counters. 3. How many more counters would you place to model a way to make 9? Draw the counters.
Lesson Check
Question 1.

Answer:
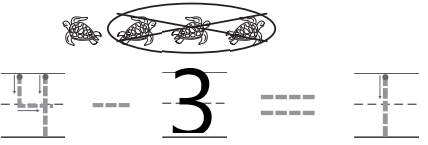
Explanation:
In the above image we can observe some tortoise. Three tortoise are taken away from the set .The left over tortoise is one. Total number of tortoise are four. The process of taking one number or amount away from another number is called as subtraction. So we have to subtract number of tortoise taken away from the set from total number of tortoise. Then we get left over tortoise. So subtract three tortoise from four tortoise. The total number of tortoise left over is one.
Spiral Review
Question 2.

Answer:

Explanation:
In the above image, we can see the number of counters in the first set are three. The number of counters in the second set are four. So circle the set that has the greater number of counters. The second set contains a greater number of counters. So, circle for the second set.
Question 3.

Answer:
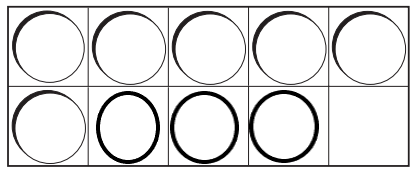
Explanation:
Three more counters are needed to place the model in a way to make nine. The addition is taking two or more numbers and adding them together. In the above image we can observe three counters are added.
Lesson 6.6 Algebra • Write More Subtraction Sentences
Essential Question How can you solve subtraction word problems and complete the equation?
Share and Show
DIRECTIONS 1–3. Listen to the subtraction word problem. How many birds are taken from the set? Trace the circle and X. How many birds are left? How many birds were there in all to begin with? Write and trace to complete the subtraction sentence.
Question 1.

Answer:
Subtract six from eight in order to get the difference. The difference is two.
Explanation:
In the above image we can observe some birds. Six birds are taken away from the set .The left over birds are two. Total number of birds are eight. The process of taking one number or amount away from another number is called as subtraction. So we have to subtract number of birds taken away from the set from total number of birds. Then we get left over birds. So subtract six birds from eight birds. The total number of birds left over are two.
Question 2.

Answer:
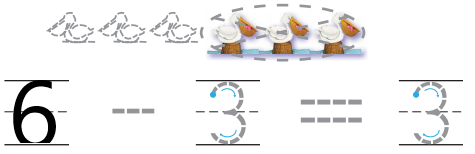
Explanation:
In the above image we can observe some birds. Three birds are taken away from the set .The left over birds are three. Total number of birds are six. The process of taking one number or amount away from another number is called as subtraction. So we have to subtract number of birds taken away from the set from total number of birds. Then we get left over birds. So subtract three birds from six birds. The total number of birds left over are three.
Question 3.

Answer:

Explanation:
In the above image we can observe some birds. Four birds are taken away from the set .The left over birds are five. Total number of birds are nine. The process of taking one number or amount away from another number is called as subtraction. So we have to subtract number of birds taken away from the set from total number of birds. Then we get left over birds. So subtract four birds from nine birds. The total number of birds left over are five.
DIRECTIONS 4–6. Listen to the subtraction word problem. How many birds are taken from the set? Trace the circle and X. How many birds are left? How many birds were there in all to begin with? Write and trace to complete the subtraction sentence.
Question 4.

Answer:
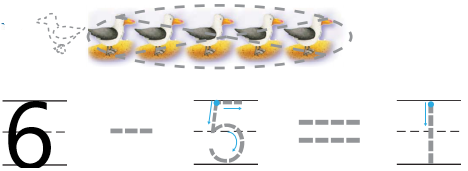
Explanation:
In the above image we can observe some birds. Five birds are taken away from the set .The left over bird is one. Total number of birds are six. The process of taking one number or amount away from another number is called as subtraction. So we have to subtract number of birds taken away from the set from total number of birds. Then we get left over birds. So subtract five birds from six birds. The total number of birds left over are five.
Question 5.

Answer:
Explanation:
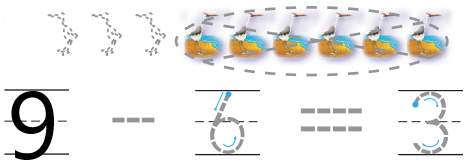
In the above image we can observe some birds. six birds are taken away from the set .Now there are three birds. Total number of birds are nine. The process of taking one number or amount away from another number is called as subtraction. So we have to subtract number of birds taken away from the set from total number of birds. Then we get left over birds. So subtract six birds from nine birds. The total number of birds left over are three.
Question 6.

Answer:
Explanation:
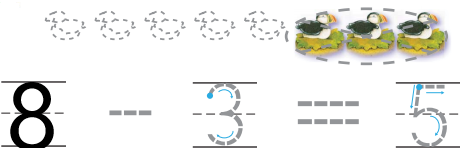
In the above image we can observe some birds. Three birds are taken away from the set .Now there are five birds. Total number of birds are eight. The process of taking one number or amount away from another number is called as subtraction. So we have to subtract number of birds taken away from the set from total number of birds. Then we get left over birds. So subtract three birds from eight birds. The total number of birds left over are five.
Problem Solving • Applications
DIRECTIONS 7. Complete the subtraction sentence. Draw a picture of real objects to show what you know about this subtraction sentence. Tell a friend about your drawing.
Question 7.

Answer:

Explanation:
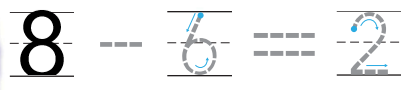
In the above image we can see eight oranges. In that six oranges are taken away from the set. Circle the animals that are taken away from the set and marked with X. In order to get the left over oranges we have to subtract six oranges from total number of oranges. Then we will get the number of oranges left over. The left over oranges are two.
HOME ACTIVITY • Tell your child you have some small objects in your hand. Tell him or her that you are taking two objects from the set and now there are five objects left. Ask him or her to tell you how many objects were in the set to start with.
Algebra • Write More Subtraction Sentences Homework & Practice 6.6
DIRECTIONS 1–3. Listen to a subtraction word problem about the birds. There are some birds. _____ birds are taken from the set. Now there are _____ birds. How many birds in all did you start with? Write the number to complete the subtraction sentence.
Question 1.

Answer:
Explanation:
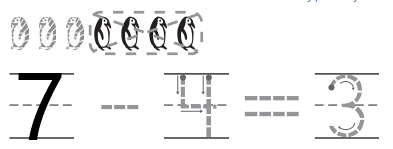
In the above image we can observe some birds. Four birds are taken from the set .Now there are three birds. Total number of birds are seven. We have to subtract number of birds taken away from the set from total number of birds. Then we get left over birds. The process of taking one number or amount away from another number is called as subtraction. So subtract four birds from seven birds. The total number of birds left over are three.
Question 2.

Answer:
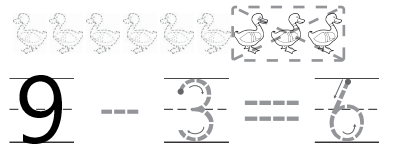
Explanation:
In the above image we can observe some birds. Three birds are taken away from the set .Now there are six birds. Total number of birds are nine. The process of taking one number or amount away from another number is called as subtraction. So we have to subtract number of birds taken away from the set from total number of birds. Then we get left over birds. So subtract three birds from nine birds. The total number of birds left over are six.
Question 3.

Answer:
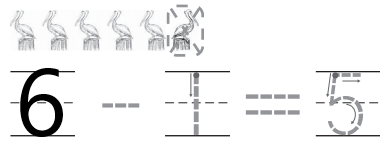
Explanation:
In the above image we can observe some birds. One bird is taken away from the set .Now there are five birds. Total number of birds are six. The process of taking one number or amount away from another number is called as subtraction. So we have to subtract number of birds taken away from the set from total number of birds. Then we get left over birds. So subtract one bird from six birds. The total number of birds left over are five.
DIRECTIONS 1. Trace and write to show the subtraction sentence for the buses. 2. How many lunch boxes are there? Write the number. 3. Count the dots in the ten frames. Begin with 1. Write the numbers in order as you count forward.
Lesson Check
Question 1.

Answer:
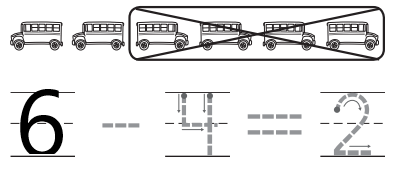
Explanation:
In the above image we can see the total number of buses are seven. In that four buses are taken away .We have to find how many buses left over there. Number of buses taken away are four and the total number of buses are six. So we have to subtract total number of buses taken away from total number of buses . Subtract four buses from six buses. So we got the left over buses. The left over buses are two.
Spiral Review
Question 2.

Answer:
Explanation:
In the above image we can observe some lunch boxes. We have to perform addition operation to calculate the total number of lunch boxes. An addition sentence is a mathematical expression that shows two or more values added together and their sum. Total number of lunch boxes are seven
Question 3.

Answer:
Explanation:
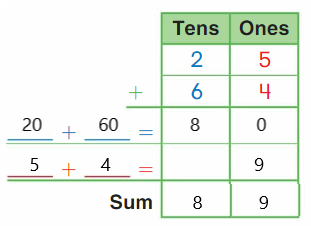
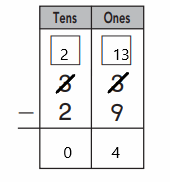
- In the first frame, we can see that there are total ten number of counters and nine are not colored grey. If we substract the number of non-colored counters from total number of counters, then we will get the total number of grey colored counters. So, substracting nine from the total ten counters gives us one grey colored counters.
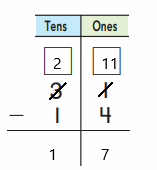
- Similar to the first frame, if we see in the second frame, there are total ten number of counters and eight are not colored grey. If we substract the number of non-colored counters from total number of counters, then we will get the total number of grey colored counters. So, substracting eight from the total ten counters gives us two grey colored counters.
- For the third frame, the same logic will apply here as well an substracting seven from ten gives us three grey colored counters.
- For the fourth frame, substracting four from the total ten counters will give us four grey colored counters.
- For the fifth frame, substracting five from the total ten counters will give us five grey colored counters.
Lesson 6.7 Algebra • Addition and Subtraction
Essential Question How can you solve word problems using addition and subtraction?
Share and Show
DIRECTIONS Tell addition and subtraction word problems. Use cubes to add and to subtract. 1. Trace the number sentences. 2. Complete the number sentences.
Question 1.

Answer:
The first cube train contains five red cubes and two blue cubes. ADD five red cubes with two blue cubes .The total number of cubes are seven.
Total number of cubes in the second cube train are seven. Subtract two blue cubes from total number of cubes are seven. Total number of red cubes are five.
Explanation:
In the first image we can see five red cubes and two blue cubes. We have to find total number of cubes. In order to get the total number of cubes we have to perform addition operation. An addition sentence is a mathematical expression that shows two or more values added together and their sum. ADD five red cubes with two blue cubes then we get total number of cubes. So the total number of cubes are seven.
In the second image we can see the total number of cubes are seven. In that two blue cubes are taken away .We have to find how many red cubes are left over there. Number of cubes taken away are two and the total number of cubes are seven. So we have to subtract total number of blue cubes taken away from total number of cubes . Subtract two blue cubes from seven cubes. So we got the left over red cubes. The left over red cubes are five.
Question 2.

Answer:

Explanation:
In the first image we can see six red cubes and four blue cubes. We have to find total number of cubes. In order to get the total number of cubes we have to perform addition operation. An addition sentence is a mathematical expression that shows two or more values added together and their sum. ADD six red cubes with four blue cubes then we got total number of cubes. So the total number of cubes are ten.
In the second image we can see the total number of cubes are ten. In that four blue cubes are taken away .We have to find how many red cubes are left over there. Number of cubes taken away are four and the total number of cubes are ten. So we have to subtract total number of blue cubes taken away from total number of cubes . Subtract four blue cubes from ten cubes. So we got the left over red cubes. The left over red cubes are six.
DIRECTIONS 3–4. Tell addition and subtraction word problems. Use cubes to add and subtract. Complete the number sentences.
Question 3.

Answer:
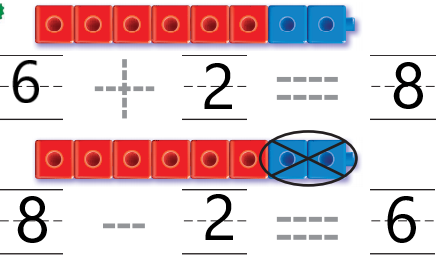
Explanation:
In the first image we can see six red cubes and two blue cubes. We have to find total number of cubes. In order to get the total number of cubes we have to perform addition operation. An addition sentence is a mathematical expression that shows two or more values added together and their sum. ADD six red cubes with two blue cubes then we get total number of cubes. So the total number of cubes are eight.
In the second image we can see the total number of cubes are eight. In that two blue cubes are taken away .We have to find how many red cubes are left over there. Number of cubes taken away are two and the total number of cubes are eight. So we have to subtract total number of blue cubes taken away from total number of cubes . Subtract two blue cubes from eight cubes. So we got the left over red cubes. The left over red cubes are six.
Question 4.

Answer:
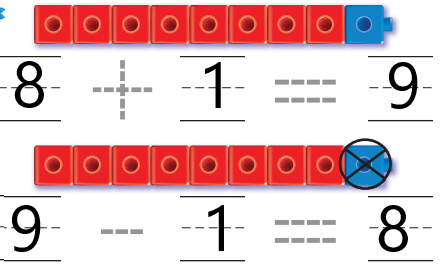
Explanation:
In the first image we can see eight red cubes and one blue cube. We have to find total number of cubes. In order to get the total number of cubes we have to perform addition operation. An addition sentence is a mathematical expression that shows two or more values added together and their sum. ADD eight red cubes with one blue cube then we get total number of cubes. So the total number of cubes are nine.
In the second image we can see the total number of cubes are nine . In that one blue cube is taken away .We have to find how many red cubes are left over there. Number of cubes taken away are one and total number of cubes are nine .So we have to subtract total number of blue cubes taken away from total number of cubes . Subtract one blue cube from nine cubes. The left over red cubes are eight .
Problem Solving • Applications

DIRECTIONS Look at the addition sentence at the top of the page. 5–6. Tell a related subtraction word problem. Complete the subtraction sentence.
Question 5.

Answer:

Explanation:
The process of taking one number or amount away from another number is called as subtraction. The result of a subtraction is called a difference. Subtraction is signified by the minus sign. For example, there are nine birds on a tree. If three birds flew away, then the number of birds left on the tree will be calculated by substracting the number of birds flew away from the total number of birds on the tree. If we substract three from six, then we get the answer as three.
Question 6.

Answer:

Explanation:
The process of taking one number or amount away from another number is called as subtraction. The result of a subtraction is called a difference. Subtraction is signified by the minus sign. For example, there are nine birds on a tree. If three birds flew away, then the number of birds left on the tree will be calculated by substracting the number of birds flew away from the total number of birds on the tree. If we substract three from nine, then we get the answer as six.
HOME ACTIVITY • Ask your child to use objects to model a simple addition problem. Then have him or her explain how to make it into a subtraction problem.
Algebra • Addition and Subtraction Homework & Practice 6.7
DIRECTIONS 1–2. Tell an addition or subtraction word problem. Use cubes to add or subtract. Complete the number sentence.
Question 1.

Answer:
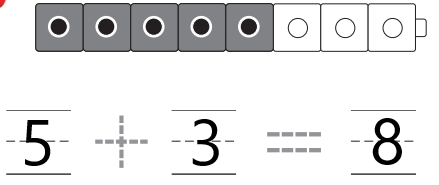
Explanation:
In the above image we can see five grey cubes and three white cubes .Perform addition to get total number of cubes. An addition sentence is a mathematical expression that shows two or more values added together and their sum. ADD five black cubes with three white cubes then we get total number of cubes. The total number of cubes are eight.
Question 2.

Answer:

Explanation:
In the above image we can see the total number of cubes are eight .Three cubes are taken away .We have to find how many cubes are left over there. Number of cubes taken away are three and total number of cubes are eight .So we have to substract total number of cubes taken away from total number of cubes . The left over cubes are five .
DIRECTIONS 1. Tell a subtraction word problem. Use cubes to subtract. Complete the number sentence. 2. Complete the addition sentence to show the numbers that match the cube train. 3. Compare the numbers. Circle the number that is greater.
Lesson Check
Question 1.

Answer:
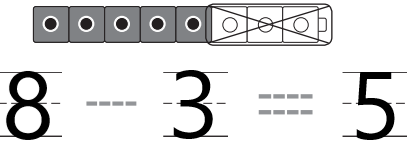
Explanation:
In the above image we can see the total number of cubes are eight .Three cubes are taken away .We have to find how many cubes are left over there. Number of cubes taken away are three and total number of cubes are eight .So we have to substract total number of cubes taken away from total number of cubes . The left over cubes are five .
Spiral Review
Question 2.

Answer:
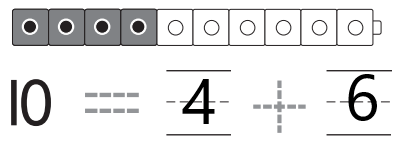
Explanation:
In the above image the total number of cubes are ten. In that image we can see four black cubes and six white cubes .Perform addition to get total number of cubes. An addition sentence is a mathematical expression that shows two or more values added together and their sum. ADD four black cubes with six white cubes then we get total number of cubes are ten.
Question 3.

Answer:

Explanation:
In the above image we can see two numbers. First one is eight and second one is nine. By comparing these two numbers nine is greater than eight .So circle it for nine.
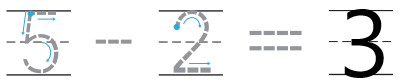
Subtraction Review/Test
DIRECTIONS 1. Write how many owls are flying away. Write how many owls are left. 2. Which answers show how many counters are red? Choose Yes or No. 3. Model a five-cube train. Two cubes are yellow and the rest are blue. Take apart the cube train to show how many are blue. Draw the cube trains. Trace and write to complete the subtraction sentence.
Question 1.

Answer:
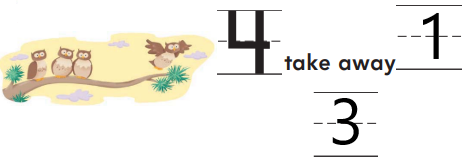
Explanation:
In the above image total number of owls on the tree are four. One owl is flying away. The number of owls left on the tree are calculated by the subtraction method. Subtract number of owls flying away from the total number of owls present on the tree which means subtract one owl from four owls. Owls left on a tree are three.
Question 2.

Answer:
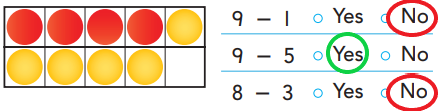
Explanation:
In the above image, we can see there are total nine counters. In that, four are red counters and five are yellow counters. We have to choose the correct answer for number of red counters by subtracting the number of yellow counters from total umber of counters. If the answer matches with the number of red counters, then the answer is ‘Yes’ or else ‘No’.
- In the first number sentence, subtracting one yellow counter from the total nine counters will not give the correct number of red counters. The answer doesn’t match with the number of red counters and so the answer is ‘No’.
- In the second number sentence, substracting five yellow counters from the total nine counters equals four red counters. So, the answer is ‘Yes’.
- In the third number sentence, substracting three yellow counters from eight counters will not give correct number of red counters. So the answer is ‘No’.
Question 3.
THINK SMARTER+

Answer:
![]()
Explanation:
In the above image we can see a five-cube train. Two cubes are yellow and the rest are blue. In order to find how many cubes are blue, we have to substract the yellow cubes from total number of cubes.
- Total number of cubes are five.
- Number of Yellow color cubes are two.
- Substracting two yellow cubes from the total five cubes will give us the total number of blue cubes which are three.
DIRECTIONS 4. There are 4 penguins. Two penguins are taken from the set. How many penguins are left? Trace and write to complete the subtraction sentence. 5. There are some birds. Three birds are taken from the set. How many birds are left? How many birds were there in all to start? Write and trace to complete the subtraction sentence. 6. Does the number sentence match the picture? Circle Yes or No. 7. Mark under all the number sentences that match the cubes.
Question 4.

Answer:
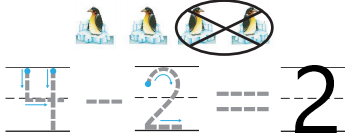
Explanation:
In the above image there are four penguins. Two penguins are taken from the set. Substract two penguins from the total four penguins and so we get left over penguins. The left over penguins are two.
Question 5.

Answer:
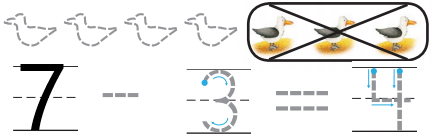
Explanation:
In the above image, the total number of birds are seven. In that, three birds are taken from the set. So, substract three birds which are taken away from the set from the total seven birds and we will get the number of birds left over in the set and they are four.
Question 6.

Answer:
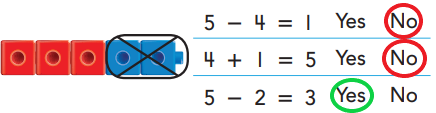
Explanation:
In the above picture, we can see a five cube train. In that, three are red cubes and two are blue cubes . The picture says that all the blue cubes are taken apart from the train and only the red cubes are remaining there.
- The first number sentence doesn’t match with the five cube train. Because in the above picture two blue cubes are taken away , So substracting four from five is not relevant here. So answer is ‘No’ for first number sentence.
- In the second sentence we can observe addition process takes place , which is irrelevant to the cube train as we are taking apart the blue cubes from the train actually. .So answer is ‘No’ for second number sentence also.
- In third number sentence, we can see total number of cubes are 5 and taken away blue cubes are two by substracting these we can get three red cubes . So answer is ‘Yes’ for third sentence.
Question 7.

Answer:
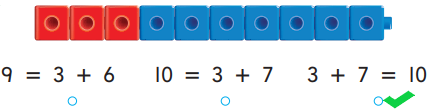
Explanation:
In the above image we can see a ten cube train and three number sentences. In that image we have to match the cube train with number sentence. A ten cube train contains three red cubes and seven blue cubes. Add three red cubes with seven blue cubes to get ten cube train which matches with the third number sentence. Mark for third number sentence.
DIRECTIONS 8. Model a four-cube train. Three cubes are red and the rest are blue. Take apart the train to show how many cubes are blue. Draw the cube trains. Complete the subtraction sentence. 9–10. Complete the subtraction sentence to match the picture.
Question 8.

Answer:
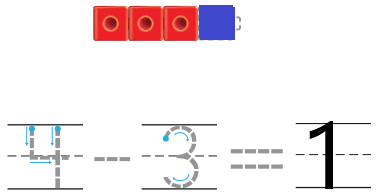
Explanation:
In the above image we can see a four-cube train. In that three cubes are red and rest are blue. In order to get how many cubes are blue ,subtract three red cubes from the total four cubes so as to get one blue cube .
Question 9.

Answer:
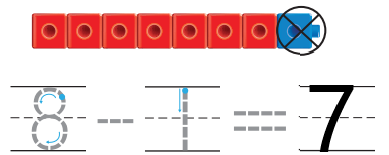
Explanation:
In the above image we can see an eight cube train . In that, one cube is blue and remaining are red. Blue cube is taken apart from the train, so substract one blue cube from the total eight cube train and then we will get the number of red cubes present in the train .The number of red cubes in the above image are seven.
Question 10.

Answer:
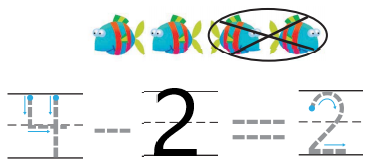
Explanation:
In the above image we can see four fish are there. In that two fish are taken away which represents to subtract two fish from four fish that we have and we will get the number of fish left over. The left over fish are two in the image.
DIRECTIONS 11. There were some apples on a tree. Some were taken away. Now there are zero apples left. Draw to show how many apples there could have been to start. Cross out apples to show how many were taken away. Complete the subtraction sentence. 12. There are some birds. Two birds are taken from the set. How many birds are left? How many birds were there in all to begin with? Write the number to complete the subtraction sentence. 13. Erica has 6 balloons. She gives some of her balloons to a friend. Now Erica has 4 balloons. How many did Erica give to her friend? Draw to solve the problem. Complete the subtraction sentence.
Question 11.
THINK SMARTER+

Answer:


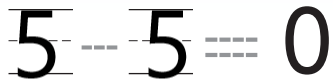
Explanation:
In the first image, we can see there are five apples on a tree and in the second image five apples are taken away. Now the apples on the tree are zero as we have taken away all the five apples.
Question 12.

Answer:
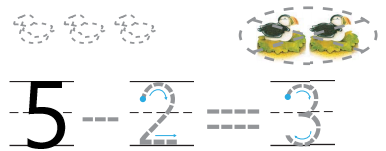
Explanation:
In the above image we can see five birds are there in total and two birds were taken away from the set. So, substract two birds from the set of five birds and then the remaining birds are three.
Question 13.

Answer:

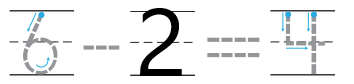
Explanation:
In the above image we can see Erica has six balloons and She gave two of her balloons to her friend. Subtract two balloons from total number of balloons are two. Now Erica has four balloons with her.































































































































































 =
= 












































 and
and 


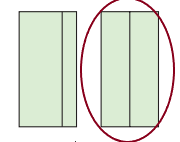



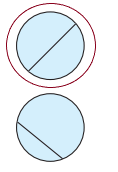



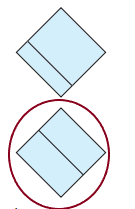
























































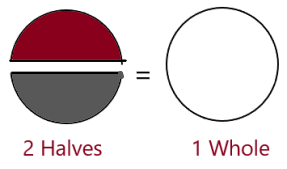







 There are 2 equal share.
There are 2 equal share.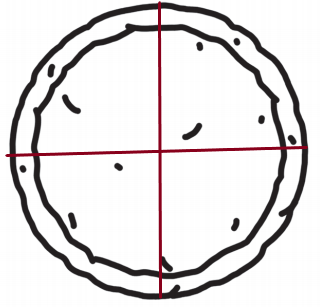 There are 4 equal shares.
There are 4 equal shares.








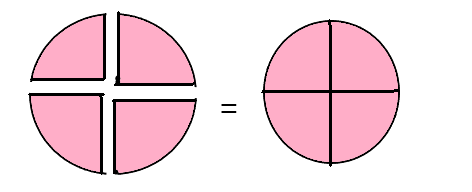



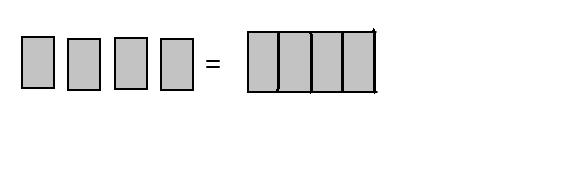


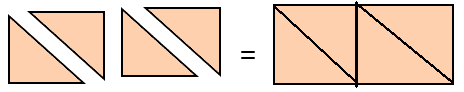











































































































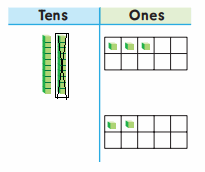

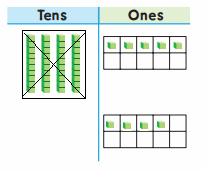

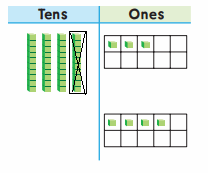

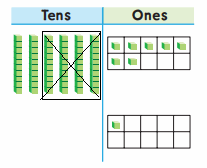

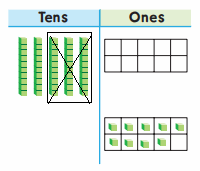







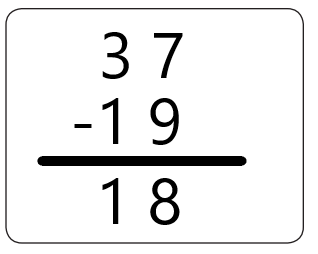









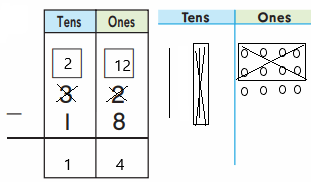

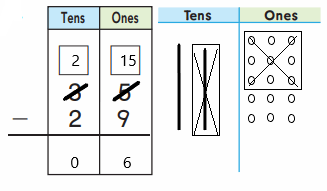















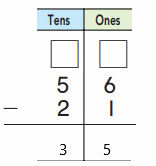





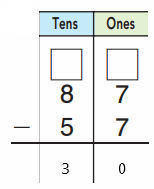

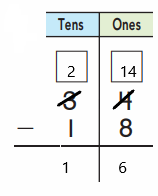

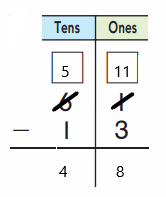



































































































 craft sticks now.
craft sticks now.





 they still have
they still have














 ___
___
 _______
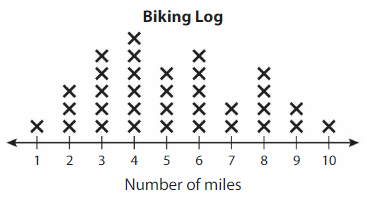
_______ __ bees
__ bees









































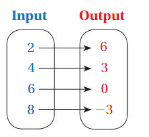

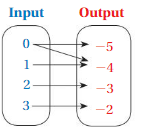
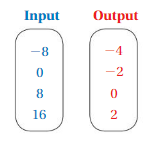
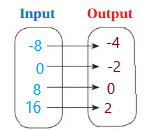
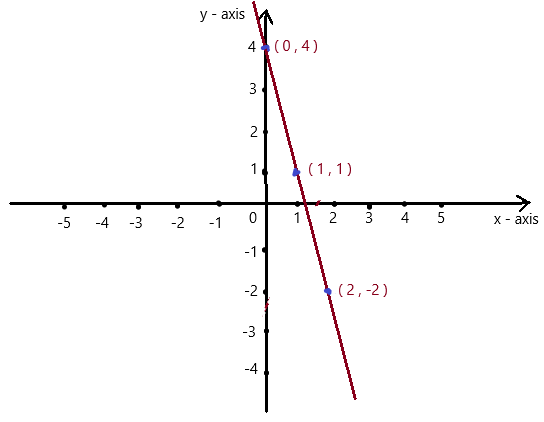
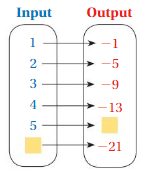
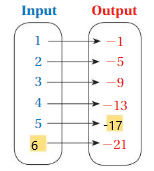
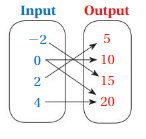
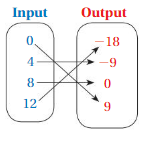
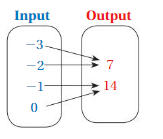
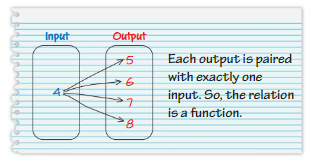


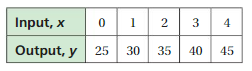
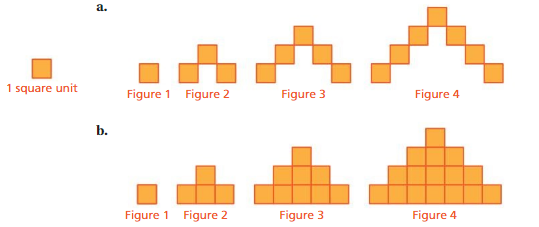




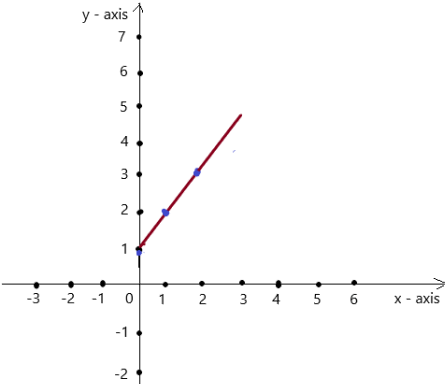
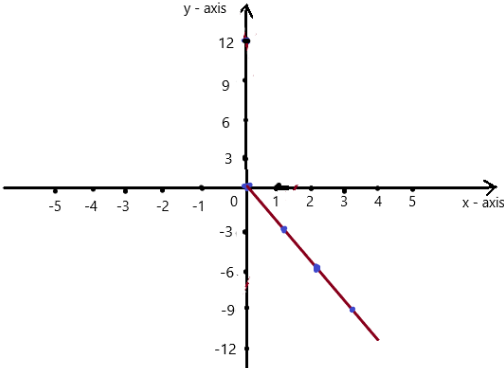
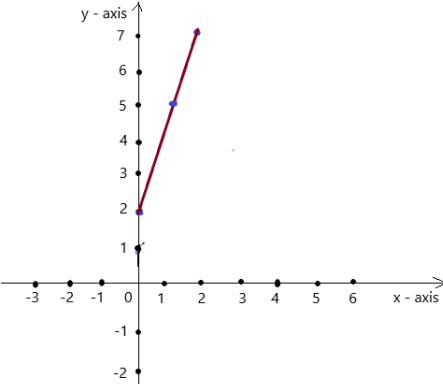
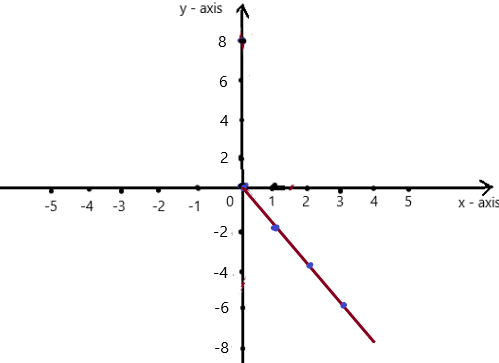

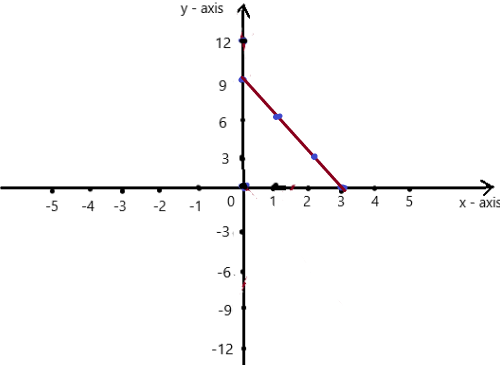


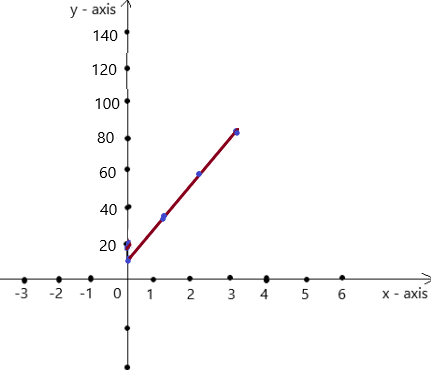
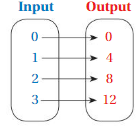
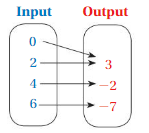
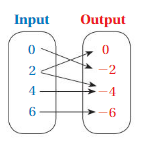

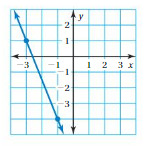
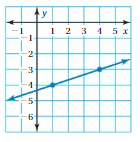

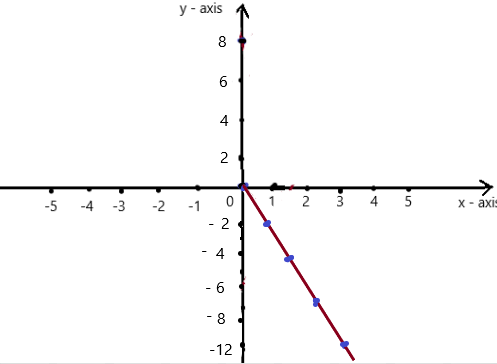
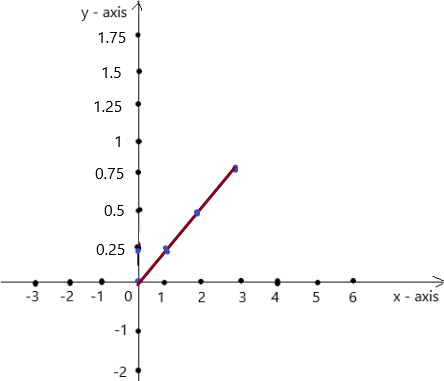

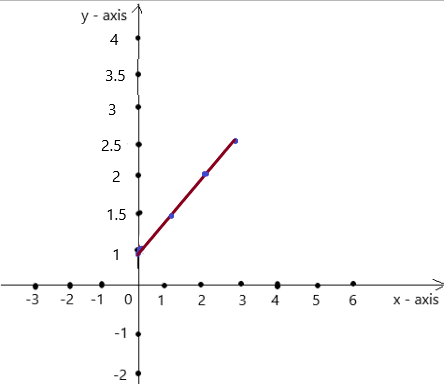

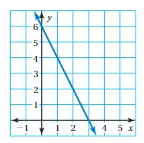
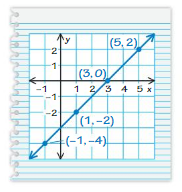
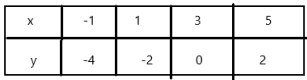

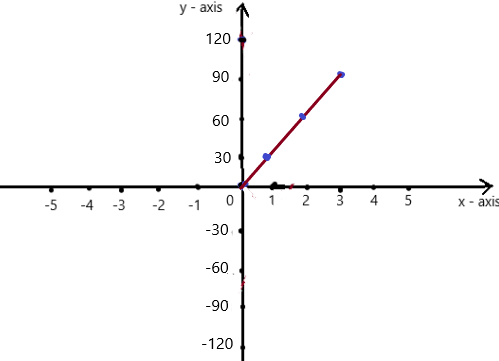

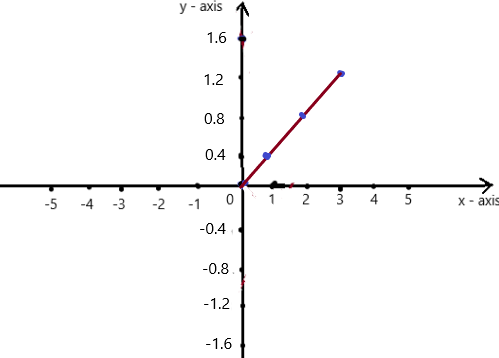


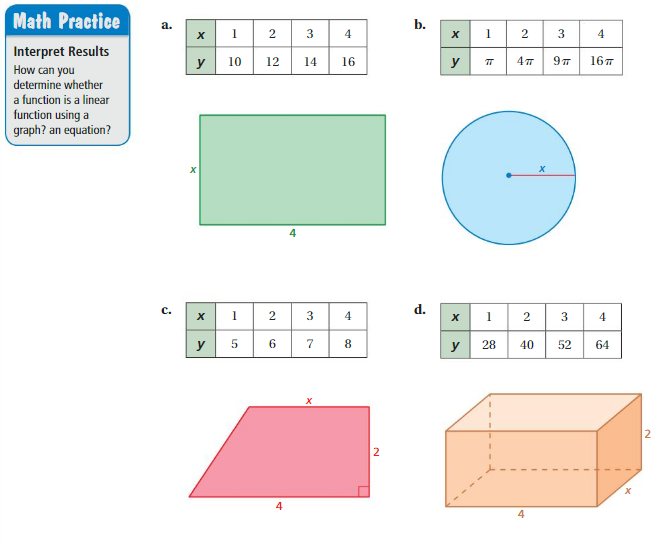




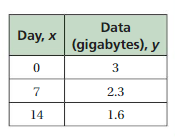
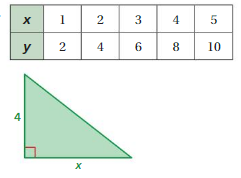


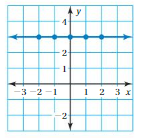
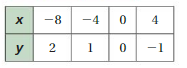
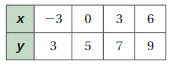
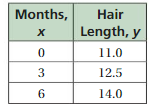
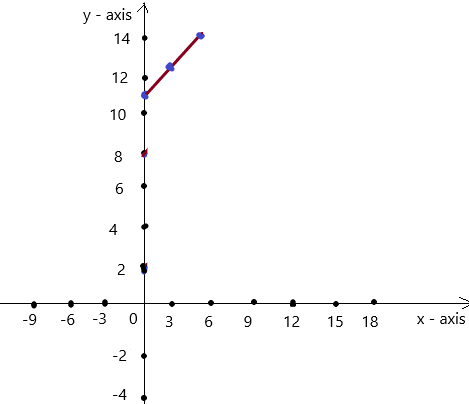
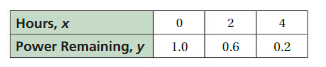
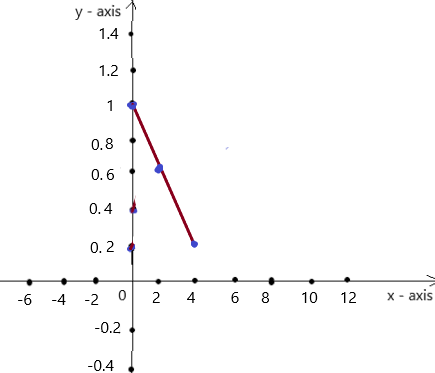



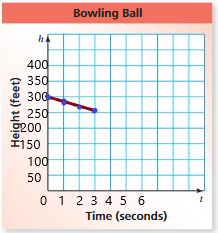

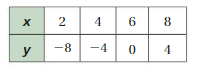

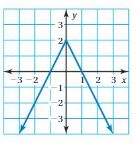
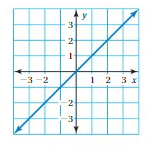
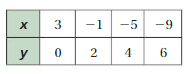
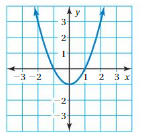




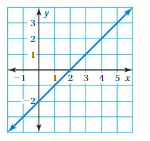



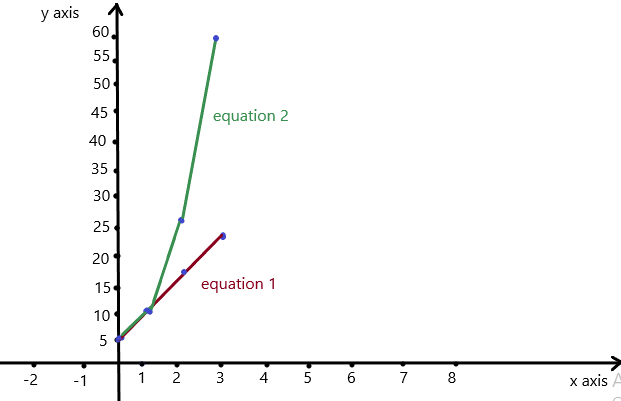
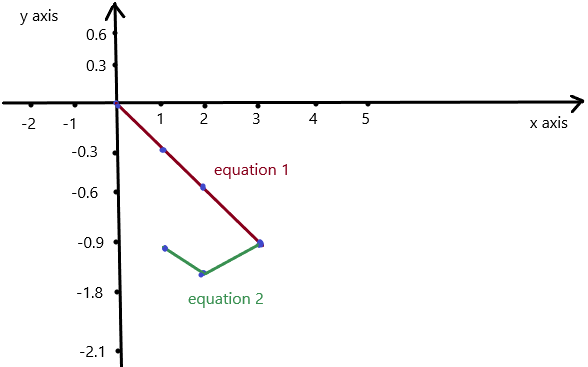


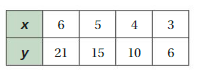
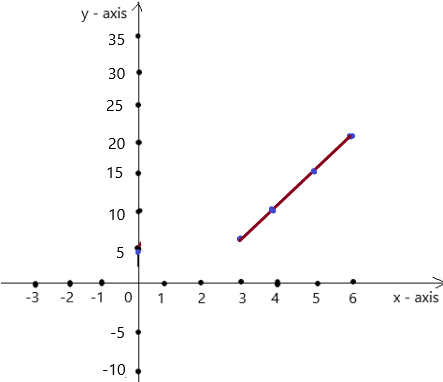
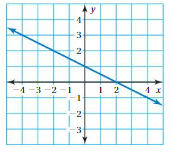

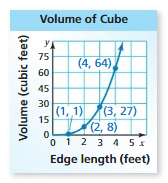
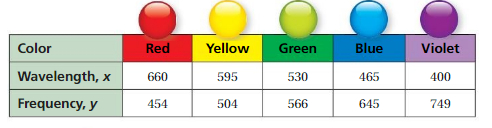

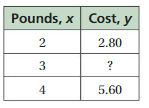
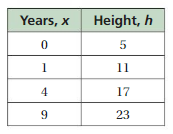

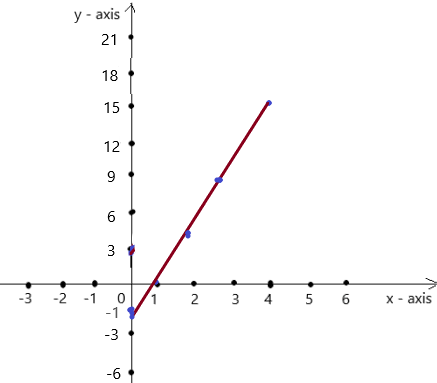

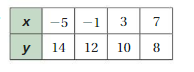
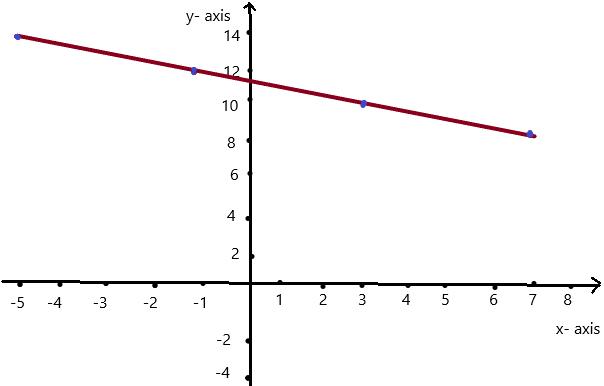








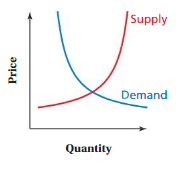

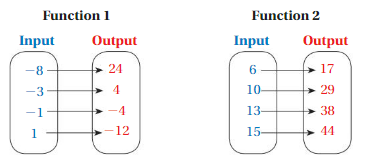
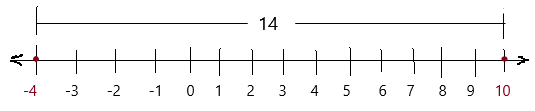
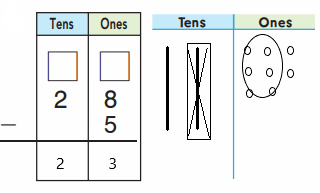
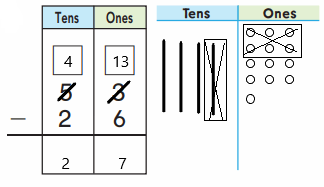
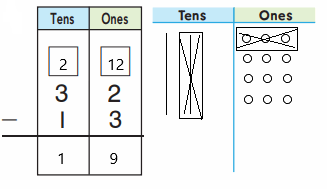
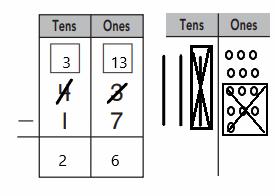
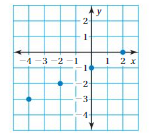
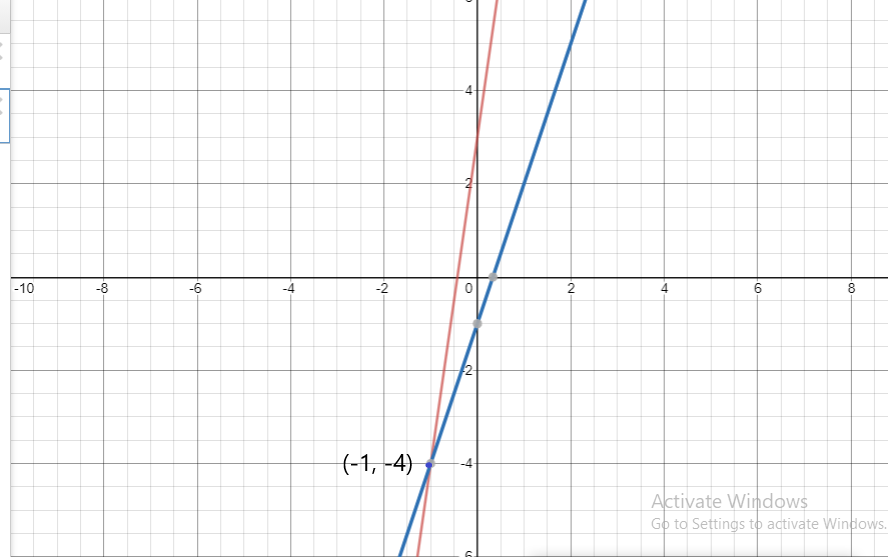 So, The point of intersection is (-1,-4).
So, The point of intersection is (-1,-4).





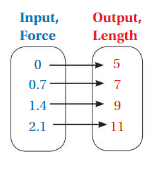
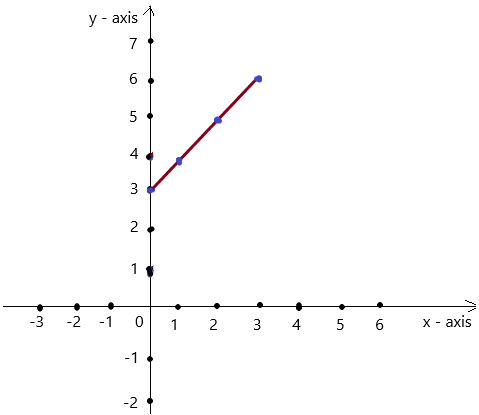
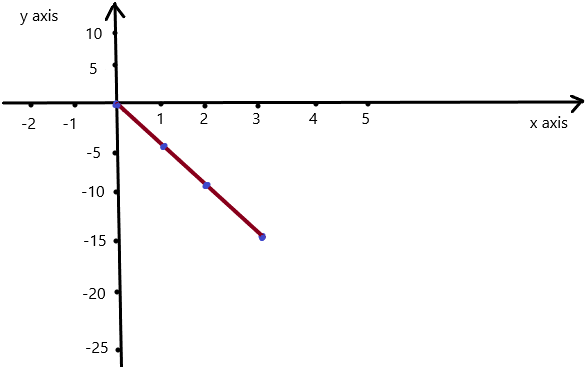
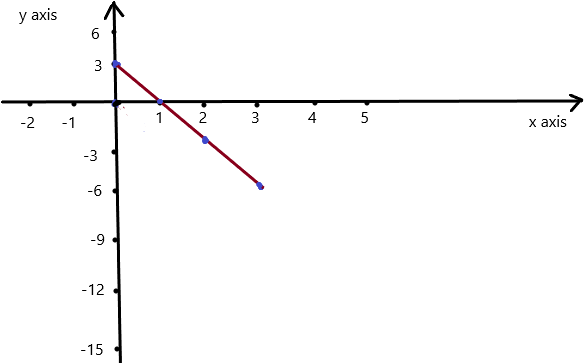




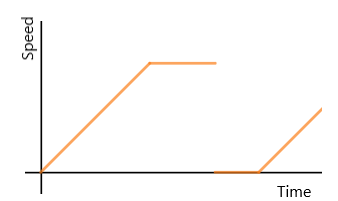

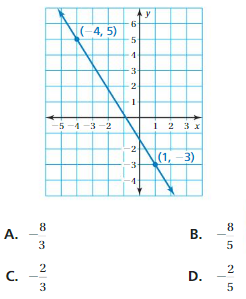
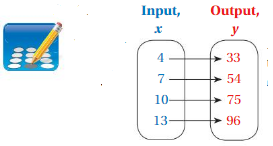
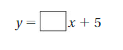
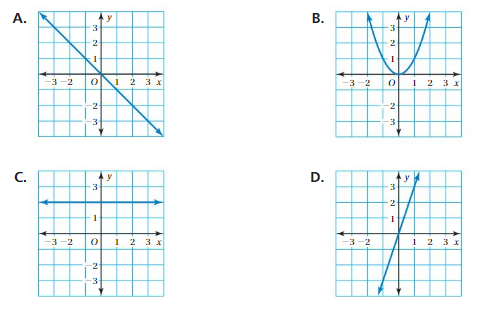
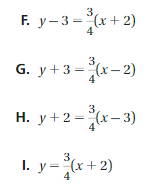

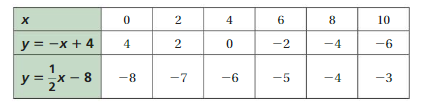

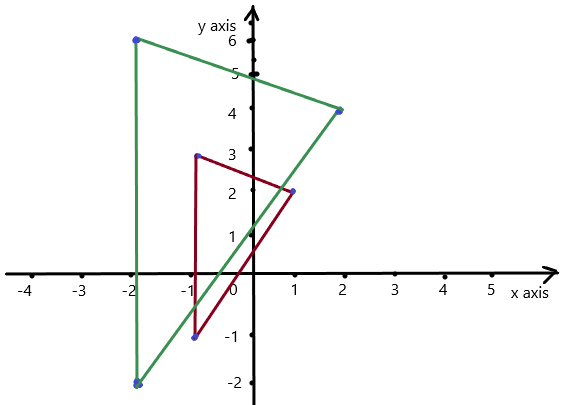


 =
= 
 =
= 
 =
= 
 =
= 
 =
= 
 =
= 
 =
=