An Irregular Figure is a figure that is not a standard geometric shape and you can’t calculate the area of them using the standard area formulas. However, some irregular shapes are formed using two or more standard geometric figures. Thus, to find the area of the irregular shapes we split them according to shapes whose formulas we know and then add the area of those figures.
Irregular Shapes Definition
Irregular shapes are polygons that have five or more sides of varying lengths. These shapes or figures can be decomposed further into squares, triangles, and quadrilaterals to evaluate the area.
How to Calculate Area of Irregular Figures?
There are various methods to calculate the Area of Irregular Shapes and we have outlined few popular ones in the below modules. They are as under
- Evaluating Area using Unit Squares
- Divide the Irregular Shapes into two or more regular shapes
- Divide the Irregular Shapes with Curves into two or more regular shapes
Evaluating Area using Unit Squares
Use this Technique if you are dealing with shapes that are curves apart from a perfect circle, semicircle, and are irregular quadrilaterals. In this technique, you need to divide the shape into unit squares. The total number of unit squares that fall within the shape determines the total area. Count the squares as 1 if the shaded region covers more than half to have an accurate estimation.

Divide the Irregular Shapes into two or more regular shapes
You can use this technique for irregular shapes that are a combination of known shapes such as triangles, polygons. Use the predefined formulas to find the area of such shapes and then add them up to know the total area.
Example:
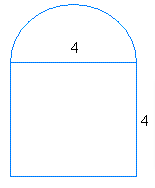
The above figure has two regular shapes square, semi circle
We can find the areas of them individually and then team up to know the Area of Irregular Shape
Given Side of a Square = 4
Area of Square = S2
Substituting the side value in the area of square formula we get
Area of Square = 42
= 16
Area of a Semi-Circle = \(\frac { 1 }{ 2 } \) π*r2
Diameter = 4
Radius = d/2 = 4/2 = 2
Area of a Semi-Circle = \(\frac { 1 }{ 2 } \)(3.14*22)
= \(\frac { 1 }{ 2 } \)(3.14*4)
= \(\frac { 1 }{ 2 } \)12.56
= 6.28
Area of Irregular Shape = Area of Square + Area of Semi Circle
= 16+6.28
= 22.28
Divide the Irregular Shapes with Curves into two or more regular shapes
In this technique decompose the given irregular shape into multiple squares, triangles, or other quadrilaterals. Based on the Curve and Shapes, part of the figure can be a circle, semi-circle, or quadrant.
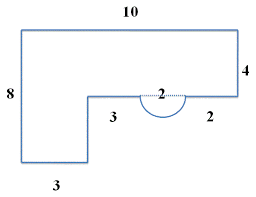
Given Irregular Shape can be divided into multiple squares, rectangles, semi-circle, etc.
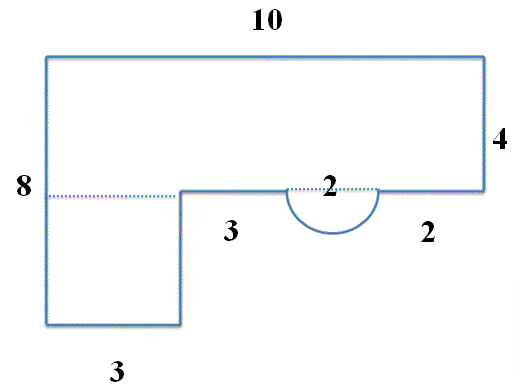
We can split the above figure into two rectangles, half circle
Let us find the area of rectangle 1
Area of Rectangle 1 = Base * Height = 4 * 10 = 40
Later find the area of rectangle 2:
Area of Rectangle 2 = Base * Height = 3 * (8 – 4) = 12
Let us find the Area of Semi Circle
A = \(\frac { 1 }{ 2 } \) π*r2
Area of Semi Circle = (1/2)(3.14)12 = 1.57
Sum up all the individual areas to get the Area of the Irregular Shape
Total Area = 40 + 12 + 1.57 = 53.57
Examples on Area of Irregular Shapes
1. Work out the Area for the following Shape?
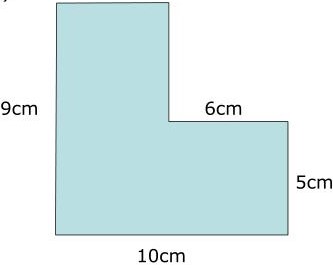
Solution:
Given Irregular Shape can be further divided into two rectangles
Area of 1st rectangle = 10*5
= 50 cm2
Area of 2nd Rectangle = (9-5)*(10-6)
= 4*4
= 16 cm2
Therefore, the Area of Irregular Shape can be obtained by combining the areas of two rectangles
Area of Irregular Shape = Area of 1st rectangle + Area of 2nd Rectangle
= 50 cm2 +16 cm2
= 66 cm2
2. Find the Area of Irregular Figure provided below?
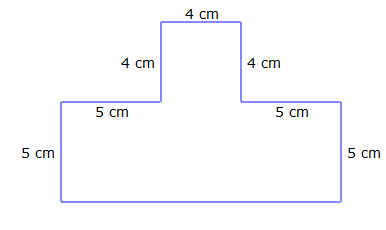
Solution:
We can split the above Irregular Figure into known shapes like Rectangle, Squares.
Firstly, find the area of the rectangle = Length* Breadth
= 5*14
= 70 cm2
Area of Square = Side2
= 42
= 16 cm2
Area of Irregular Figure = Area of Rectangle + Area of Square
= 70 cm2+ 16 cm2
= 86 cm2