An Area is a space or a region occupied by any shape. Square is a two-dimensional figure with four sides, it is also known as a quadrilateral. The area of a square is defined as the number of square units needed to fill a square. In other words, a square is a product of two sides, length, and breadth that are equal. In the square, all four angles are also equal. Square has four equal sides and four vertices. The diagonals of the square are equal and bisect each other at 90 degrees, angles of the square are equal to 90 degrees. If a square is cut by a plane from the center, then both halves are symmetrical.
Learn completely about the Area of a Square Definition, Formula, and Units. Get to know the Properties of a Square, Solved Examples on How to Calculate the Area of a Square, etc.
Do Read: Practice Test on Area and Perimeter of Square
Area of a Square – Definition
The area of a square is defined as the total number of unit squares in the shape of a square. A Square is a rectangle whose length and breadth are equal which means all four sides are equal.
 Area of a Square Formula
Area of a Square Formula
The area of a square formula is used for calculating the occupied region. It is measured in square units.
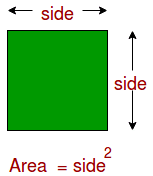
Area of a square=side x side
Perimeter of a Square Formula
The perimeter of the square is equal to the sum of all its four sides. The unit of the perimeter remains the same as that of the side-length of a square.
Perimeter=side+side+side+side=4side unit
Perimeter =4 x side of the square = 4a unit
Where ‘a’ is the length of the side of the square.
Also, Read: Perimeter of a Square
Length of Diagonal of a Square
The length of the diagonals of the square is equal to s√2, where s is the side of the square. The length of the diagonals is equal to each other. By Pythagoras theorem, diagonal is the hypotenuse and the two sides of the triangle formed by the diagonal of the square, are perpendicular and base. Hypotenuse²=Base² + Perpendicular²
Hence,Diagonal²=side² + side²
Diagonal=√2side², d=s√2
where d is the length of the diagonal of a square and s is the side of the square.
Diagonal of Square
It is a line segment that connects two opposite vertices of the square. Suppose we have four vertices, thus we can have two diagonals within a square. The diagonal of a square is always greater than its sides.
The relation between Diagonal ‘d’ and Side ‘a’ of a square is, d=a√2
The relation between Diagonal ‘d’ and Area ‘A’ of a square is, d=√(2A)
The relation between Diagonal ‘d’ and Perimeter ‘P’ of a square is,d=p/2√2
Area of Square Units
Usually, the Area of the Square is measured in the Square Units since each side of the square is the same. Some of the Common Units of Measurement and their equivalent are expressed below.
- 1 m=100 cm
- 1 sq.m=10,000 sq.cm
- 1 km=1000 m
- 1 sq.km=1,000,000 sq.m
Properties of a Square
Have a glance at the Properties of Square and get an idea of them so that you might find them useful while solving related problems. They are as follows
- The square has 4 vertices and 4 sides.
- All four interior angles are equal to 90⁰.
- The opposite sides of the square are parallel to each other.
- The two diagonals of the square are equal to each other.
- The length of diagonals is greater than the sides of the square.
Solved Problems on Area of a Square
1. Find the Area of a square of the Side 2.5 cm?
Solution:
Given, Area of a square of the side is 2.5 cm
Area of a square = length x length
Substitute the given value in the above formula,
= 2.5 x 2.5 sq. cm
= 6. 25 sq. cm
2. Find the area of a square of side 49 m?
Solution:
Given, Area of a square of the side is 49 m
Area of a square = length x length
Substitute the given value in the above formula,
= 49 x 49 sq. m.
= 2401 sq. m.
3. Let a square has a side equal to 3 cm. Find out its area, length of diagonal, and perimeter?
Solution:
Given, side of the square, s= 3 cm
Area of a square= s²
Therefore, by substituting the value of the side, we get,
3² = 9 cm²
Length of the diagonal of square = s√2
By substituting the value, we get,
3 x 1.414 = 4.242
The perimeter of the square = 4 xs
substituting the value in the above formula, we get,
4 x 3= 12 cm.
4. Find the area of a square clipboard whose side measures 120 cm?
Solution:
Given, side of the clipboard = 140 cm = 1.4 m
Area of the clipboard = side x side
substituting the value in the above formula, we get,
Area of the clipboard = 140 cm x 140 cm
= 19,600 sq . cm
= 1.96 sq . m
5. A wall that is 40 m long and 30 m wide is to be covered by square tiles. The side of each tile is 2 m. Find the number of tiles required to cover the wall?
Solution:
Given, Length of the wall = 40 m
The breadth of the wall = 30 m
Area of the wall = Length x breadth
substituting the length and breadth values, we get
Area of the wall= 40 m x 30 m = 1200 sq. m
side of one tile = 2 m
Area of one tile = side x side
substitute the value in the above formula, we get
Area of one tile =2 m x 2 m= 4 sq. m
No. of tiles required = Area of wall/ Area of a tile
substitute the value, we get
No.of tiles required = 1200/ 4 = 300 tiles
FAQ’s on Area of a Square
1. What is the Area of a Square Formula?
The area of a square can be calculated by using a formula side x side square units.
2. Define Perimeter and Area of a Square?
The perimeter of a square is the sum of all the four sides of a square, whereas the Area of a square is defined as the region or the space occupied by a square in the two-dimensional space.
3. How is a Square different from a Rectangle?
A square has all its sides are equal in length whereas a rectangle has only its opposite sides are equal in length.
4. What are the real-life examples of a Square?
Some of the real-life examples of a square are Carrom Board, Square tiles, Square shaped tables, Cubes, Chess Board, etc.
